Modellingpg1

Ammonia

The molecule of ammonia was optimised using RB3LYP calculation method and 6-31G(d,p) basis set. The point group of the molecule is C_3v and its lowest energy was found to be -56.55776873 a.u. Also, the bond length and angle were determined and compared to experimantal values (see the table below) and it can be concluded that the theoretically determined values are highly accurate as the percentage error is less than 1 % in both cases.

Structure

Ammonia molecule
	Calculated values	Experimental values	% error
Bond length [Å]	1.01798	1.012	0.59
Bond angle [°]	105.741	106.7	0.90
Optimisation data

It was also checked that the optimisation was successful by looking at the values of the maximum force and displacement: since these values are very close to zero and below the threshold, it can be confirmed that the forces and displacements in the structure were converged and the optimisation was finished properly (see table below).

Item table of ammonia

Item	Value	Threshold	Converged?
Maximum Force	0.000004	0.000450	Yes
RMS Force	0.000004	0.000300	Yes
Maximum Displacement	0.000072	0.001800	Yes
RMS Displacement	0.000035	0.001200	Yes

Frequency analysis

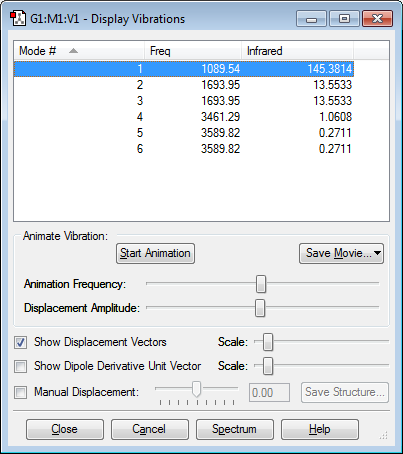
Frequency analysis shows six vibrational modes which matches the number of modes predicted by the 3N - 6 rule where N = 4 as ammonia is a molecule consisting of four atoms (3x4-6=6). They all have a positive sign which confirms that the optimisation was successful. There are two pairs of degenerate vibrational modes: number 2 and 3, and number 5 and 6. Modes 1, 2, and 3 are bending vibrations while modes 4, 5 and 6 are bond stretch vibrations. Also, mode 4 is highly symmetric and mode 1 is the so called umbrella mode. As for the experimental IR spectrum of ammonia in the gaseous state, only 2 bands are expected to be observed, which is because of two reasons: first of all, there are two pairs of degenerate frequencies which lowers the number from six to four. Second of all, the intensities of the vibrations have to be considered: the intensities of vibrations 4 and 6 are very low (around 1 or below) so these bands would be extremely small and unidentifiable. These intensities are so low because of the small change in dipole moment that results from the vibrations.

Charge analysis

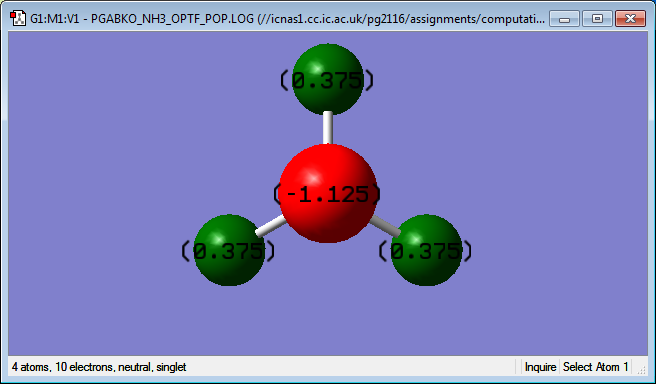
Charge analysis shows the following distribution of charges in the molecule: the nitrogen atom has a -1.125 charge and each hydrogen atom has a 0.375 charge. The signs of the charges match the prediction: since nitrogen is more electronegative than hydrogen, it shifts the electron density from the hydrogen atoms towards itself and obtains a negative charge while hydrogen atoms become partially positively charged as they lost some electron density.

Haber-Bosch process

The Haber-Bosch process is a process in which ammonia is produced from nitrogen and hydrogen gas in the following reaction:

N₂ + 3H₂ → 2NH₃

Determining the thermodynamic parameters of this process is key for setting the most suitable conditions for the reaction so that the costs are minimized while the yield is maximized. Therefore, the energy difference for this process was calculated by determining the energies of hydrogen and nitrogen gas and subsequent subtraction of energies of the reactants from the products. First, the molecular structures of nitrogen and hydrogen were optimised by selecting D_∞h point group and using RB3LYP calculation method and 6-31G(d,p) basis set. After that, it was checked that the forces and displacements in the structures are converged (see tables below) and that the optimisation was successful by confirming all vibrational frequencies were positive values. Both molecules showed only one vibration which was the bond stretch vibration and the values were found to be 4465.68 cm^-1 and 2457.33 cm^-1 for hydrogen and nitrogen respectively. However, these frequencies would not be observed in an IR spectrum because the bond stretches do not cause a change in the dipole moment as the molecules are homonuclear diatomic. This was also confirmed by the fact that the intensities were zero in both cases. As for the difference between the vibrational frequencies, it could be explained by the term (k/µ)^1/2 in the frequency calculation formula where k is the force constant and µ is reduced mass. The bond in the nitrogen molecule is a triple bond while there is only a single bond in the hydrogen molecule so more energy is required to stretch the nitrogen molecule. Therefore, it could be expected that the force constant and vibrational frequency would be higher in case of nitrogen but the opposite was observed. This is probably due to the reduced mass, which is much lower in case of hydrogen and offsets the relatively large force constant in nitrogen. Therefore, the vibration frequency of hydrogen is much higher.

Item table of nitrogen

Item	Value	Threshold	Converged?
Maximum Force	0.000001	0.000450	Yes
RMS Force	0.000001	0.000300	Yes
Maximum Displacement	0.000000	0.001800	Yes
RMS Displacement	0.000000	0.001200	Yes

Item table of hydrogen

Item	Value	Threshold	Converged?
Maximum Force	0.000000	0.000450	Yes
RMS Force	0.000000	0.000300	Yes
Maximum Displacement	0.000000	0.001800	Yes
RMS Displacement	0.000001	0.001200	Yes

Finally, the energy of the molecules was determined and the energy difference for the reaction was calculated:

E(NH₃) = -56.55776873 a.u.

2xE(NH₃) = -113.1155375 a.u.

E(N₂) = -109.52412868 a.u.

E(H₂) = -1.17853936 a.u.

3xE(H₂) = -3.53561808 a.u.

ΔE = 2xE(NH₃)-[E(N₂)+3xE(H₂)] = -0.05579074 a.u.

The value of the energy difference can be converted to kJ/mol as these units are preferred for energy differences so the value in a.u. was multiplied by 2625.5:

ΔE = -146.48 kJ/mol

Based on the negative value of the energy difference, it can be deduced that the reaction is exothermic and that the product is lower in energy and more stable than the reactants. After comparing the result with an experimentally determined enthalpy change, a large difference was observed as the experimental value is -91.82 kJ/mol. This difference was attributed to the fact that GaussView assumes temperature of 0 K when carrying out the calculations while the experimental value was measured under standard conditions.

Fluorine

The molecule of fluorine was optimised using RB3LYP calculation method and 6-31G(d,p) basis set. The point group of the molecule is D_∞h and its lowest energy was found to be -199.49825218 a.u. The bond length was compared with an experimental value (see the table below) and it can be concluded that the theoretically determined value is quite accurate as the percentage error is only about 3 %.

Structure

Fluorine molecule
	Calculated value	Experimental value	% error
Bond length [Å]	1.40281	1.36	3.1
Optimisation data

Also, by checking that the forces and displacements in the structure were converged (see table below), it was confirmed that the optimisation was finished properly.

Item table of fluorine

Item	Value	Threshold	Converged?
Maximum Force	0.000128	0.000450	Yes
RMS Force	0.000128	0.000300	Yes
Maximum Displacement	0.000156	0.001800	Yes
RMS Displacement	0.000221	0.001200	Yes

Frequency analysis

The fluorine molecule showed only one vibration at frequency 1065.09 cm^-1 and it was the bond stretch vibration. Since the frequency has a positive value, it can be concluded that the optimisation was successful. As in the case of nitrogen or hydrogen, this frequency would not be observed in an IR spectrum as the molecule is homonuclear diatomic so the bond stretch does not result in a change in dipole moment. If the vibrational frequency is compared to the ones of nitrogen and hydrogen, it can be observed that it is the lowest. This is for two main reasons: first of all, fluorine is the heaviest molecule of them so it has the largest reduced mass. Second of all, fluorine has only a single bond and lots of lone electron pairs which repel each other quite a lot since it is a small molecule so the bond is relatively weak and hence the force constant is also relatively small.

Charge analysis

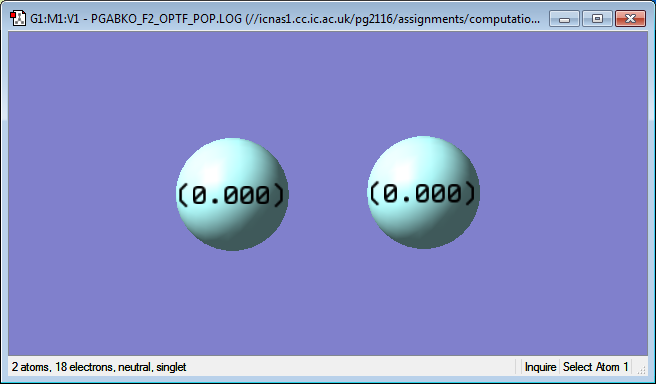
After running a charge analysis, it was found that both fluorine atoms carry no charge. This matched the expectation as the molecule is homonuclear diatomic so the bond is 100% covalent and there is no shift in the electron density.

Molecular orbitals

The analysis of molecular orbitals showed nine fully occupied orbitals from which two pairs were degenrate and one empty orbital. Pictures of five of these are included below and commented on:

This bonding molecular orbital is the lowest in energy (-24.79730 a.u.) and is the combination of two 1s atomic orbitals. Since it is a combination of two core orbitals, they do not contribute to bonding much and do not form one extended surface.

Unlike the first molecular orbital, this one is much higher in energy (-1.33659 a.u.) and forms one extended surface because it is a combination of two 2s atomic orbitals which are valence. Therefore, the overlap is much better and contributes more to bonding. Also, it is a bonding molecular orbital.

This bonding molecular orbital is a combination of two 2p atomic orbitals and contributes to the sigma bond of the fluorine molecule. It is slightly higher in energy than the previous one (-0.58753 a.u.), quite close to the HOMO/LUMO region.

This is a bonding molecular orbital and is a combination of two 2p atomic orbitals which overlap perpendicularly to the sigma bond so it contributes to π bonding. There is also another bonding molecular orbital of this type which is formed perpendicular to the sigma bond but in the other direction. Therefore, these two orbitals and degenerate and their energy is -0.52332 a.u. which is close to the HOMO/LUMO region.

The last molecular orbital is the antibonding version of the 2p - 2p atomic orbital combination along the sigma bond. It is the lowest uncuppied molecular orbital (-0.12679 a.u.) so its effect on bonding is extremely small.