ModellingJN1316
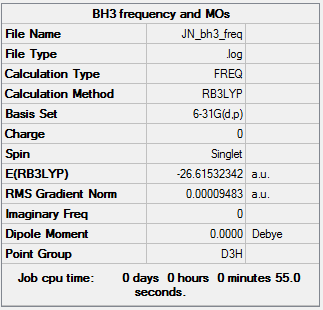
BH3
Method b3lyp Basis 6-31g(d,p)
Item Value Threshold Converged?
Maximum Force 0.000190 0.000450 YES
RMS Force 0.000095 0.000300 YES
Maximum Displacement 0.000747 0.001800 YES
RMS Displacement 0.000374 0.001200 YES
Predicted change in Energy=-2.125549D-07
Optimization completed.
-- Stationary point found.
Low frequencies --- -0.2260 -0.1035 -0.0054 48.0278 49.0875 49.0880 Low frequencies --- 1163.7224 1213.6715 1213.6741
test molecule |
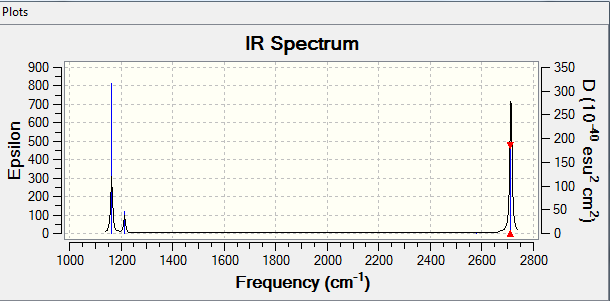
Mode Freq Infrared Active? 1 1163.72 92.4740 Y 2 1213.67 14.0890 Y 3 1213.67 14.0926 Y 4 2579.74 0.00000 N 5 2712.67 126.4185 Y 6 2712.67 126.4089 Y
There are 6 modes but only 3 peaks this is because mode 4 is inactive, 2 and 3 are degenerate and 5 and 6 are degenerate.
Source: www.huntresearchgroup.org.uk
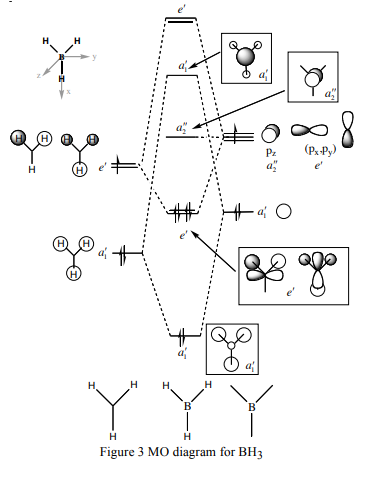
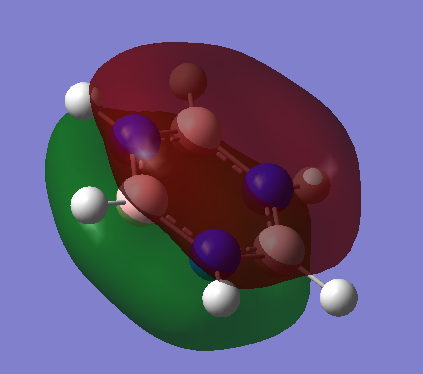
The diagram shows there is little difference between the LCAO MO's and the real MO's (see below) therefore qualitative MO theory is an accurate and useful approximation.
Ng611 (talk) 19:51, 15 May 2018 (BST) Unfortunately you've forgotten to add the real MOs.
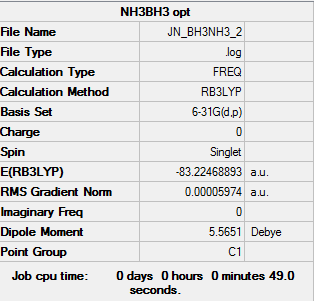
NH3BH3 Item table Item Value Threshold Converged? Maximum Force 0.000021 0.000120 YES RMS Force 0.000014 0.000500 YES Maximum Displacement 0.000601 0.001200 YES RMS Displacement 0.000274 0.001100 YES
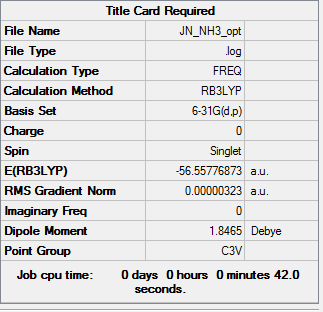
NH3 Item table Item Value Threshold Converged? Maximum Force 0.000002 0.000180 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000006 0.001200 YES Low frequencies --- -11.6527 -11.5490 -0.0045 0.0332 0.1512 26.5724 Low frequencies --- 1080.6616 1694.5736 1594.1736
E(NH3) = -56.55776873 a.u. E(BH3) = -26.61532342 a.u. E(NH3BH3) = -83.22468893 a.u. dE = E(NH3BH3) - [E(NH3)+E(BH3)] dE = 0.05159678 a.u. = 135.46 kJ/mol Therefore it is a weak bond for example C-C is 346 kJ/mol
Ng611 (talk) 19:54, 15 May 2018 (BST) Your answers should be to the nearest Kj/mol as this is the maximum level of accuracy that can be achieved with DFT. Your comparison is good but remember to include a literature source for your bond strength (ideally a textbook or a paper).
DSPACE: DOI:10042/202329
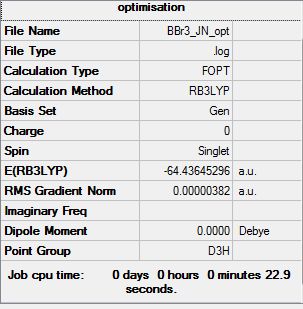
BBr3 Item table Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES Low frequencies --- -0.0137 -0.0094 -0.0046 2.5315 2.4315 5.8421 Low frequencies --- 155.9651 156.9651 277.7152
Project Section: Aromatics
test molecule |
test molecule |
| Benzene | Borazine | Comparison | |
|---|---|---|---|
 |
 |
MO 7 for both benzene (left) and borazine (right) are similar in shape and energy. It is all in phase bonding with from s orbitals in both cases as there is only 1 phase. N being more electronegative than B draws density away from the B-H bonds and reduces the overall summetry of the MO. The reduced electron density over Boron bonded Hydrogens means they are not involved in the MO. Borazine is lower in energy (-0.88852 hartrees) than benzene (-0.84677) due to the polarity of the bonds causing an increased electrostatic attraction between the atoms. Because this is a purely MO and Nitrogen is lower in energy than carbon it has a greater contribution form the nitrogen as it is closer in energy to this bonding MO. | |
 |
 |
MO 17 for benzene (left) and borazine (right) are very similar in shape and similar in energy. Borazine is lower (-0.36129 hartrees) in energy than Benzene (-0.35998). The orbitals are the combination of 6 p orbitals in a conjugated pi ring. It is a bonding orbital. There is a slight bulge in electron density over nitrogen compared to boron in borazine due to its higher electronegativity, this causes the MO to be lower in energy due to the increased electrostatic attraction between nitrogen and boron. There is no contribution from the hydrogens as they have no p orbitals. | |
 |
 |
MO14 for benzene (left) and borazine (right) are similar in shape and energy. Borazine (-0.43198 hartrees) is significantly lower than benzene (-0.35998 hartrees). This is an antibonding MO with antibonding sigma orbitals between the C-C bonds and B-N bonds. The absolute values of energy as misleading as the negative values suggest these MOs are favourable, the uncertainty in the calculations means we can only compare the difference between MOs on the same basis. The borazine is lower in energy as there is worse sigma overlap along the B-N axis so therefore it has less antibonding character. | |
 |
 |
MO21 for benzene and MO 20 borazine are similar in shape and energy. It is an antibonding MO that results from the combination of p orbitals. 3 p orbitals are in phase and 3 are out of phase therefore there are 2 nodal planes through the MO. No Hydrogens are involved in the MOs as they have no p orbitals. There is more distorsion and less symmetry in borazine’s MOs due to the size difference in boron and nitrogen pz orbitals. One of the lobes in the borazine MO is larger than the other as it contains 2 nitrogens and 1 boron whereas the other contains 2 borons and 1 nitrogen. Nitrogen has a higher electronegativity so attracts more density towards itself. Borazine (-0.27591 hartrees) has a lower energy than benzene (-0.24691 hartrees) due to the electronegativity difference in boron and nitrogen cuasing a stronger electrostatic attraction between the atoms. |
| Benzene | Borazine | Comparison | |
|---|---|---|---|
 |
 |
Benzene (RED = carbon, GREEN = Hydrogen) is more symmetrically charged as all the carbons have the same electronegativity as each other. The charge difference along the C-H bond (+0.239, -0.239) is low and this is a non-polar bond.
In borazine (RED = nitrogen, GREEN = boron, BLUE/DARK GREEN = Hydrogen) there is a significant charge difference between boron and nitrogen (0.747, and -1.102 respectively) reflecting the difference in their electronegativity. Hydrogens attatched to Nitrogen have electron density withdrawn (0.432) into the pi system. Boron donates a small amount of electron density to its hydrogens (-0.077). This charge difference increases the bond strength as the oppositely charged nitrogen and boron have a stronger electrostatic attraction. |
Ng611 (talk) 20:02, 15 May 2018 (BST) Your MO analysis is good. Remember to specify the direction of the p-orbitals (are they aligned with the bond, perpendicular to the plane, etc.) though!
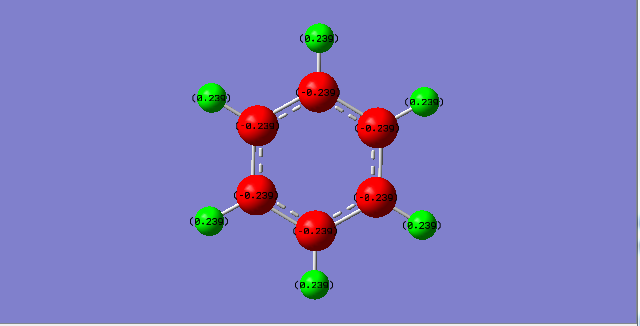
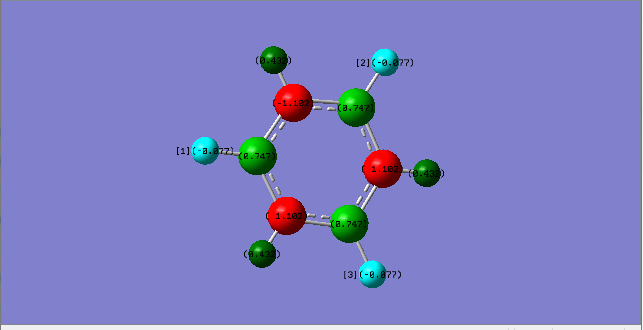
Ng611 (talk) 20:02, 15 May 2018 (BST) Charge analysis also good but you should mention that the sum of the partical charges is 0.
Aromaticity
Aromatic molecules are traditionally defined as flat, cyclic structures with an associated resonance energy that otherwise aliphatic compounds do not have. Aromaticity arises in Benzene, C6H6 as the 6 adjacent p orbitals combine by side on pi bonding to form a delocalised ring of electron density. The resultant system is the quantum mechanical average of all of the canonical forms. Hückel's rule predicts the systems that will experience aromaticity. It states the number of pi electrons in the system must equal 4n+2 where n is a number. The added stability of aromatic systems makes them resistant to electrophilic addition reactions that affect classical alkenes. Modern chemistry has a more nuanced and complex view of aromaticity, it can come in various forms and is not limited to a simple flat system of overlapping pz orbitals. A quasi-aromatic ring can be formed with a 5 atom chain hydrogen bonding to a 6th atom such as hydrogen or lithium. For 50 years scientists have considered the important role of the sigma bond in aromaticity but the subject is still debated. One example of the complexity of aromaticity is the chair conformation of benzene at low temperatures stabilised by its intermolecular interactions. This goes against the classical rule of a planar molecule.
Ng611 (talk) 19:59, 15 May 2018 (BST) You've touched on a few interesting points here, but you need to expand on them somewhat. How exactly are modern views on aromaticity more complex? What is the quantum mechanical understanding of aromaticity? How can we confirm aromaticity in these molecules (NMR, bond enthalpies etc.).
Ng611 (talk) 20:03, 15 May 2018 (BST) This has the makings of a very good report, but needed a bit more time and attention. Your first section in particular was missing key data for structures, MOs etc. The second section was much improved though!