Modelling364
Optimisation of NH3
optimised ammonia molecule |
| Data Type | Value |
|---|---|
| Molecule | NH3 |
| Calculation Method | RB3LYP |
| Basis Set | 6-3IG(d.p) |
| Final Energy (au) | -56.55776873 |
| RBM gradient | 0.00000485 |
| Point group | C3V |
| N-H bond distance (Angstroms) | 1.01798 |
| HNH bond angle (degrees) | 105.741 |
Optimised NH3 Data - Item Section
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986283D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
The optimisation file is liked to File:Dr1415 nh3 opt 1.LOG
Questions (NH3)
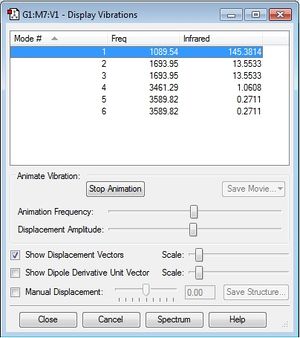
1. Using the 3N-6 rule I would expect there to be 6 modes. 2. Modes 2 and 3 are degenerate. 3. Modes 1, 2 and 3 are bending frequencies, modes 4, 5 and 6 are stretching frequencies. 4. Mode 4 is the most symmetric mode of vibration. 5. Mode 1 is the umbrella mode. 6. I would expect to see 4 bands in an infrared spectrum for gaseous ammonia because there are four modes of vibration that have different energies and hence difference corresponding frequencies.
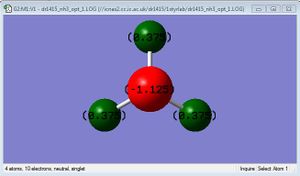
It would be expected that the nitrogen atom has a more negative charge than the hydrogen atoms because it is more electronegative, hence attracting the electrons in the N-H bond towards itself more strongly than the hydrogen atoms, and the nitrogen also has a lone pair of electrons, which since are non bonding, have a very high charge density. These expectations agree with the values of charge given in the Gaussian optimisation.
Gaussian optimisation of a molecule of N2
| Data Type | Value |
|---|---|
| Molecule | N2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-3IG(d.p) |
| Final Energy (au) | -109.52412868 |
| RBM gradient | 0.00000060 |
| Point group | D∞h |
| N-N bond distance (Angstroms) | 1.10550 |
| HNH bond angle (degrees) | 180.00 |
Optimised N2 Data - Item Section
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401049D-13
Optimization completed.
-- Stationary point found.
Optimised N2 Vibrational Frequencies
There is one mode of vibration (stretching) of frequency 2457.33 Hz. There is no corresponding IR peak because this vibration involves no change in dipole moment.
Gaussian optimisation of a molecule of H2
| Data Type | Value |
|---|---|
| Molecule | H2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-3IG(d.p) |
| Final Energy (au) | -1.17853936 |
| RBM gradient | 0.00000017 |
| Point group | D∞h |
| N-N bond distance (Angstroms) | 0.74279 |
| HNH bond angle (degrees) | 180.00 |
Optimised H2 Data - Item Section
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164081D-13
Optimization completed.
-- Stationary point found.
Optimised H2 Vibrational Frequencies
There is one mode of vibration (stretching) of frequency 4465.68 Hz. There is no corresponding IR peak because this vibration involves no change in dipole moment.
Calculating Energy Change in the Haber-Bosch Process
| Molecule/s | Energy (a.u.) |
|---|---|
| E(NH3) | -56.55776873 |
| 2*E(NH3) | -113.1155375 |
| E(N2) | -109.52412868 |
| E(H2) | -1.17853936 |
| 3*E(H2) | -3.53561808 |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] | -0.05579074 |
Hence energy change in the Haber-Bosch process is -146.48 kJ mol-1. The product is more stable than the reactants because the energy change is negative, indicating that energy is lost from the system as the reaction proceeds, hence the ammonia is in a lower energy state than the H2 and the N2. However, J. Modak reports an enthalpy change value for the Haber-Bosch process at 298K as -45.7 kJ mol-1[1]
- ↑ Jayant M. Modak, 2002, Haber Process For Ammonia Synthesis, Resonance, 7, 9, 70, available from http://link.springer.com/article/10.1007%2FBF02836187?LI=true, date accessed: 04/03/2016.
. This is a large difference from the Gaussview calculated energy change because the reported value considers temperature, and the Gaussview calculation only take into account the energies of the different MO systems, ignoring temperature. This shows that this method may not be effective for calculating energy changes in reactions.
H=U+PV
-
H+dH=U+dU+PV+dPV+PdV+dPdV
-
dH=dU+dPV+PdV
-
assume constant volume
-
dH=dU+dPV
At higher temperatures, molecules gain kinetic energy and collide with the walls of the container more frequently. Hence pressure increases and enthalpy is affected by temperature.
Examining Molecular Orbitals of N2






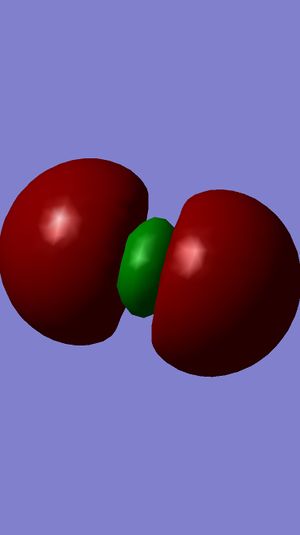
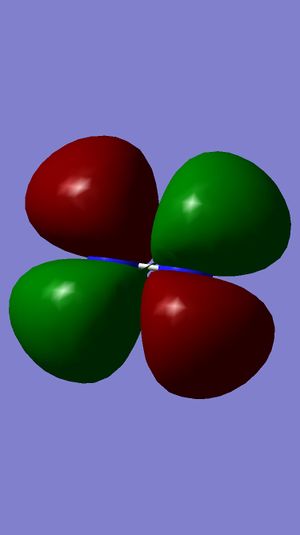


It can be seen from the Gaussian MO representations that The bond between the two nitrogen atoms is a triple bond, made up of the 1πu, 2πu and 3σg orbitals, because the bonding character of the 1σg and 2σg bonding orbitals is cancelled by the antibonding character of the 1σ*u and 2σ*u orbitals, as these are filled and the energy difference between atomic orbitals and antibonding MOs is greater than between AOs and bonding MOs. Also, the 1π*g, 2π*g and 3σ*u are not filled as they are higher energy than the 1πu, 2πu and 3σg orbitals.
Carrying Out Analysis of BH3
BH |
| Data Type | Value |
|---|---|
| Molecule | BH3 |
| Calculation Method | RB3LYP |
| Basis Set | 6-3IG(d.p) |
| Final Energy (au) | -26.61532364 |
| RBM gradient | 0.00000211 |
| Point group | D3H |
| N-H bond distance (Angstroms) | 1.19232 |
| HNH bond angle (degrees) | 120.000 |
Item section of GaussView optimised BH3
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000017 0.001800 YES
RMS Displacement 0.000011 0.001200 YES
Predicted change in Energy=-1.053682D-10
Optimization completed.
-- Stationary point found.
Vibrational Modes of BH3
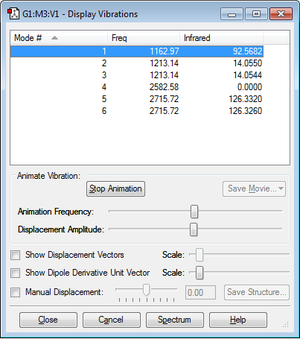
Using the 3N-6 rule it would be expected that there would be 6 vibrational modes. This agrees with the frequencies outputted by Gaussview. Modes 1, 2 and 3 are bending modes and modes 4, 5 and 6 are stretching modes. Mode 4 has no infrared peak because the stretch is highly symmetrical and causes no change in dipole moment. Modes 2 and 3 are degenerate and so are modes 5 and 6. It would be expected to see 3 peaks in an IR spectrum because the 4th mode does not yield a peak and 2/3 and 4/6 are very similar to the point where the peaks would be indistinguishable.
Charge Distribution of BH3
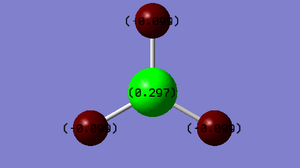
It is expected that the boron has a greater positive charge relative to the hydrogen atoms because the boron in BH3 is electron deficient - it does not have a complete octet in the valence shell, there are only 6 electrons present. For this reason, BH3 quickly dimerises and exists as B2H6.
Molecular Orbitals of BH3 (Bonding and Non-Bonding)

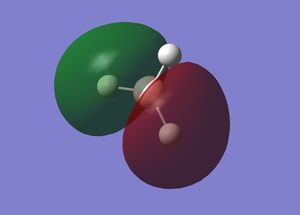

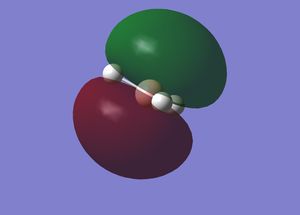
Interpretation of MO Gaussview representations
A is the 1s2 non-bonding orbital on the boron. This orbital is non-bonding because the energy is very low, due to boron having a relatively large nucleus, and the 1s orbital is highly penetrating due to having no shielding as it is the lowest energy orbital. Hence, the 1s electrons are strongly attracted to the nucleus. The next lowest energy orbital is B, which is a 1σg orbital. The MO covers the entire molecule, showing that the structure is delocalised. The electrons from the 1s orbitals of the hydrogen all partially contribute to a sigma bond with the 2s orbital of boron. In the bonding case, all of these orbitals are in phase, allowing bonding to occur and accounting for the shape of the orbital shown by Gaussview. C is the 1σu orbital. This MO in ungerade because it is a sigma bond between the 2pz AO of boron and the 1s orbitals of hydrogen. In this case, because the p orbital has two lobes which are out of phase, each of the hydrogen atoms within the MO has the same phase as the lobe of the p orbital it is overlapping with to form the bond. The hydrogen that does not appear to be within the MO contributes partially to both orbitals. D is the 2σu MO. This is formed in a similar way to C, but different 1s [H] orbitals have different phases and overlap with the 2py orbital such that the two 1s orbitals of the hydrogen atoms in the green section of the MO are in phase with each other and that lobe of the p orbital and the single 1s orbital of the hydrogen in the red section of the MO is out of phase with the other two [H]1s orbitals and in phase with the opposite lobe of the p orbital. This p orbital is the LUMO. MOs C and D are degenerate, both with energies of -0.35079 eV. These are hence both HOMOs. MO B is more stable, with an energy of -0.51254 eV because it is a more highly delocalised system. The 1s[B] orbital is clearly highly stable and it can be seen why it is non-bonding because it has an energy of -6.77140 eV.
Comment on BH3 Antibonding MOs (Gaussview)
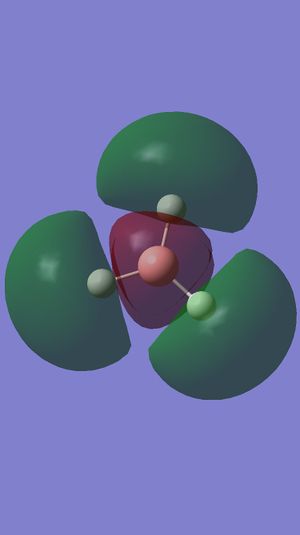
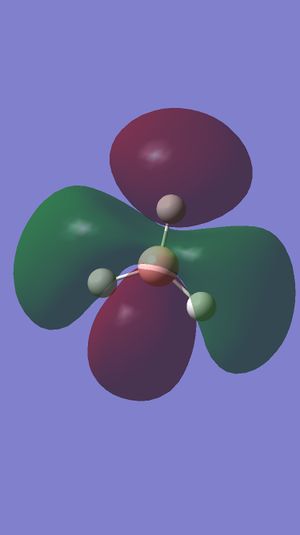
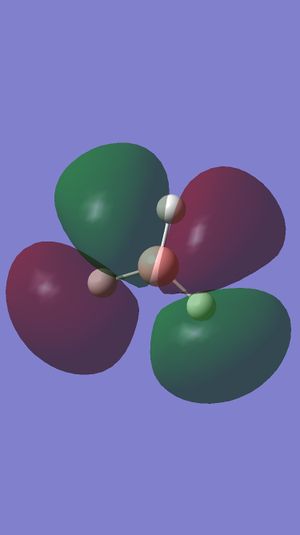
These antibonding orbitals correspond to bonding orbitals shown in the subsection above. The difference is that the orbitals that were previously in phase as described above are now out of phase and hence form antibonding rather than bonding orbitals. Energy values must also be considered. F has an energy value of +0.16839 eV, and since C and D are degenerate, so are G and H are also, with energy values of +0.17926eV. If the antibonding orbitals were filled they would have a higher energy value than the corresponding bonding orbitals and the bonding orbitals would be overcome, hence the bond would break.
