Model01405209
NH3
Data
NH3 |
| Molecule | NH3 |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) (a.u.) | -56.55776873 |
| RMS Gradient (a.u.) | 0.00000485 |
| Point Group | C3v |
| N-H bond distance (10-10 m) | 1.01798 |
| H-N-H bond angle (degrees) | 105.741 |
Item table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986282D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Frequency analysis
| Number of modes as per 3N-6 | 6 |
|---|---|
| Degenerate modes | 2 and 3 (bending), 5 and 6 (stretching) |
| Bending modes | 1, 2, 3 |
| Stretching modes | 4, 5, 6 |
| Highly symmetric mode | 4 |
| Umbrella mode | 1 |
| Expected number of IR spectrum bands | 2 (corresponding to the non-degenerate bending modes) |
While there should theoretically be 4 non-degenerate vibrations, only 2 bands are practically observable, corresponding to modes 1 (umbrella bend) and modes 2, 3 (degenerate asymmetrical bends). The higher intensity associated with these modes is due to the large change in dipole moment as the molecule vibrates.
Modes 4 (symmetrical stretch) and 5 and 6 (degenerate asymmetrical stretch) are not practically observable. In the case of these modes, due to most of the vibrational motion being in the same plane and opposite directions, there is little net change in the overall dipole moment of the molecule.
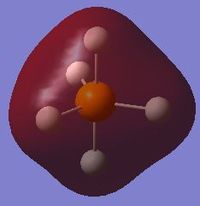
Charge distribution
| Atom | Charge (e-) |
|---|---|
| N | -1.125 |
| H | 0.375 |
The N atom is expected to have a negative charge and the H atoms are expected to have a positive charge. This is due to N being more electronegative and drawing electron density towards itself and also having unpaired electrons.
H2
Data
H2 |
| Molecule | H2 |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) (a.u.) | -1.17853935 |
| RMS Gradient (a.u.) | 0.00003809 |
| Point Group | D*h |
| H-H bond distance (10-10 m) | 0.74289 |
Item table
Item Value Threshold Converged?
Maximum Force 0.000066 0.000450 YES
RMS Force 0.000066 0.000300 YES
Maximum Displacement 0.000087 0.001800 YES
RMS Displacement 0.000123 0.001200 YES
Predicted change in Energy=-5.726834D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7429 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Frequency analysis
H2 is IR inactive: it is a linear, non-polar molecule, presenting only a (symmetrical) stretch mode at 4464.36 cm-1, according to the 3N-5 rule.
N2
Data
N2 |
| Molecule | N2 |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) (a.u.) | -109.52412868 |
| RMS Gradient (a.u.) | 0.00000060 |
| Point Group | D*h |
| N-N bond distance (10-10 m) | 1.10550 |
Item table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401076D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Frequency analysis
N2 is IR inactive: it is a linear, non-polar molecule, presenting only a (symmetrical) stretch mode at 2457.33 cm-1, according to the 3N-5 rule.
Haber process calculation
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853935 a.u.
3*E(H2)= -3.53561805 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579073 a.u. = -146.48 kJ*mol-1
Since ΔE<0, the reaction to form NH3 from N2 and H2 is overall exothermic. However, it would not take place under standard conditions, due to the unreactive nature of N2, owing to its triple bond.
BH3
Data
BH3 |
| Molecule | BH3 |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) (a.u.) | -26.61532364 |
| RMS Gradient (a.u.) | 0.00000211 |
| Point Group | D3h |
| B-H bond distance (10-10 m) | 1.19232 |
| H-B-H bond angle (degrees) | 120.000 |
Item table
Item Value Threshold Converged?
Maximum Force 0.000066 0.000450 YES
RMS Force 0.000066 0.000300 YES
Maximum Displacement 0.000087 0.001800 YES
RMS Displacement 0.000123 0.001200 YES
Predicted change in Energy=-5.726834D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7429 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Frequency analysis
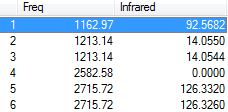
| Number of modes as per 3N-6 | 6 |
|---|---|
| Degenerate modes | 2 and 3 (bending), 5 and 6 (stretching) |
| Bending modes | 1, 2, 3 |
| Stretching modes | 4, 5, 6 |
| Highly symmetric mode | 4 |
| Umbrella mode | 1 |
| Expected number of IR spectrum bands | 3 (umbrella bend, degenerate asymmetrical stretches and degenerate asymmetrical bends) |
BHN3 presents the same vibrational modes as the previous NH3, however 3 bands are observable due to its different structure. The umbrella bend (mode 1) and asymmetrical stretches (modes 5 and 6) cause the greatest variation in dipole moment, while the degenerate asymmetrical bends (modes 2 and 3) cause a small change in dipole moment, which may not be observable. The highly symmetric stretching (mode 4) produces no change in dipole moment and is not observable in the IR spectrum.
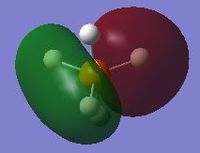
Charge distribution
| Atom | Charge (e-) |
|---|---|
| B | 0.297 |
| H | -0.099 |
The B atom is expected to have a positive charge and the H atoms are expected to have a negative charge, as H is more electronegative and draws electron density away from the central B atom. However, since the molecule is trigonal planar and symmetrical, this does not result in a permanent dipole moment.
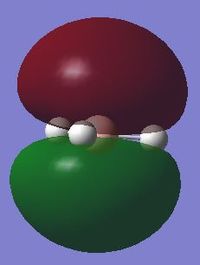
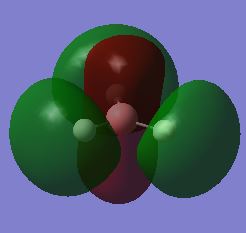
Molecular orbitals
| Image | Orbital type | Comment |
|---|---|---|
 |
Non-bonding | The 1s orbital on the B atom is far lower in energy than its other orbitals and as such does not participate in the interactions with the 1s orbitals on the H atoms. |
 |
Bonding (B 2s and H 1s orbitals) | The three bonding orbitals of BH3 result from the 2s and 2 of the 2p orbitals on B (that lie coplanar with the 1s orbitals on the H atoms). All 6 valence electrons lie in these three bonding orbitals.
While the difference in electronegativity between B and H is small, since H is more electronegative, the bonding orbitals present higher electron density on the H atoms. The image shows the lower-energy bonding orbital, formed by the interaction with the 2s orbital on B. |
  |
HOMO / bonding (B 2px, 2py and H 1s orbitals) | There are 2 degenerate, higher-energy bonding orbitals formed through interaction between the three 1s orbitals on H and two perpendicular p-orbitals on B. One of the 2p orbitals lies on the same axis as one of the B-H bonds and the other lies perpendicular to it, in the plane of the molecule. |
 |
LUMO / non-bonding (B 2pz) | The LUMO on BH3 is a non-bonding orbital; specifically, the 2p orbital of B that lies perpendicular to the plane of the molecule. Due to its orientation, it cannot efficiently overlap with the 1s orbitals on H for a bonding interaction.
In other B compounds, such as BCl3, this empty orbital can strengthen the bonds, ny interacting with the similarly oriented 2p orbitals on Cl. |
 |
Antibonding (B 2s and H 1s orbitals) | This is the higher-energy antibonding orbital, corresponding to the lower-energy bonding orbital. As B is more electropositive than hydrogen, this orbital would feature increased electron density around the central B atom, however this orbital is unoccupied. |
PH5
Data
PH5 |
| Molecule | PH5 |
|---|---|
| Calculation method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Final energy E(RB3LYP) (a.u.) | -344.25491049 |
| RMS Gradient (a.u.) | 0.00000471 |
| Point Group | D3h |
| N-H axial bond distance (10-10 m) | 1.48687 |
| N-H equatorial bond distance (10-10 m) | 1.43316 |
| H-P-H axial bond/equatorial plane angle (degrees) | 90.000 |
| H-P-H equatorial bond angle (degrees) | 120.000 |
Item table
Item Value Threshold Converged?
Maximum Force 0.000009 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000055 0.001800 YES
RMS Displacement 0.000022 0.001200 YES
Predicted change in Energy=-1.032822D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4332 -DE/DX = 0.0 !
! R2 R(1,3) 1.4869 -DE/DX = 0.0 !
! R3 R(1,4) 1.4869 -DE/DX = 0.0 !
! R4 R(1,5) 1.4332 -DE/DX = 0.0 !
! R5 R(1,6) 1.4332 -DE/DX = 0.0 !
! A1 A(2,1,3) 90.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 90.0 -DE/DX = 0.0 !
! A3 A(2,1,5) 120.0 -DE/DX = 0.0 !
! A4 A(2,1,6) 120.0 -DE/DX = 0.0 !
! A5 A(3,1,5) 90.0 -DE/DX = 0.0 !
! A6 A(3,1,6) 90.0 -DE/DX = 0.0 !
! A7 A(4,1,5) 90.0 -DE/DX = 0.0 !
! A8 A(4,1,6) 90.0 -DE/DX = 0.0 !
! A9 A(5,1,6) 120.0 -DE/DX = 0.0 !
! A10 L(3,1,4,2,-1) 180.0 -DE/DX = 0.0 !
! A11 L(3,1,4,2,-2) 180.0 -DE/DX = 0.0 !
! D1 D(2,1,5,3) 90.0 -DE/DX = 0.0 !
! D2 D(2,1,6,3) -90.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -90.0 -DE/DX = 0.0 !
! D4 D(2,1,6,4) 90.0 -DE/DX = 0.0 !
! D5 D(2,1,6,5) 180.0 -DE/DX = 0.0 !
! D6 D(3,1,6,5) -90.0 -DE/DX = 0.0 !
! D7 D(4,1,6,5) 90.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Frequency analysis
| Number of modes as per 3N-6 | 12 |
|---|---|
| Degenerate bending modes | 1 and 2 (equatorial scissoring), 4 and 5 (axial scissoring), 6 and 7 (axial rocking and equatorial wagging and twisting, respectively) |
| Degenerate stretching modes | 11 and 12 (asymmetrical equatorial stretching) |
| Bending modes | 1-7 |
| Stretching modes | 8-12 |
| Highly symmetric modes | 8 (axial lengthening/shortening and equatorial shortening/lengthening) and 10 (simultaneous axial and equatorial lengthening/shortening) |
| Umbrella mode | 3 |
| Expected number of IR spectrum bands | 5 (modes 1 and 2 (degenerate), 3, 4 and 5 (degenerate), 9, 11 and 12(degenerate)) |
5 IR spectrum bands are expected, corresponding to the above vibration modes that are not degenerate and result in a change of dipole moment. Thus, modes 6 and 7 (degenerate), 8, 10 are oscillations that do not produce such a change and are IR inactive.
Charge distribution
| Atom | Charge (e-) |
|---|---|
| P | 0.412 |
| H (axial) | -0.183 |
| H (equatorial) | -0.015 |
The axial and equatorial H atoms lie in different chemical environments, as evidenced by their different charges.
Molecular orbitals
The orbitals of P having principal quantum numbers 1 and 2 are too deep in energy and as such are non-bonding in the PH5 molecule. These would have the usual representations (spherical 1s and 2s orbitals and dumbbell-shaped 2p orbitals aligned with the x, y and z axes) and are not presented here.
| Image | Orbital type | Comment |
|---|---|---|
 |
Bonding (P 3s and H 1s orbitals) | This is the lowest energy bonding orbital, formed through the interaction between the P 3s and all five H 1s orbitals. |
  |
Bonding (P 3px, 3py and equatorial H 1s orbitals) | There are two degenerate, higher-energy bonding orbitals formed through interaction between the three 1s orbitals on the equatorial H atoms and two perpendicular 3p orbitals on P. One of the 3p orbitals lies on the same axis as one of the equatorial P-H bonds and the other lies perpendicular to it, in the equatorial plane of the molecule. |
 |
Bonding (P 3pz and axial H 1s orbitals) | This is a 3-centre bonding orbital formed through interaction between the two 1s orbitals on the axial H the 3pz orbital on P. This orbital is higher in energy than the equatorial bonding orbitals formed with the 3p orbitals on P. |
 |
HOMO / bonding (B 3dz2 and axial H 1s) | The HOMO in PH5 is another 3-centre bonding orbital resulting from the interaction between the 3dz2 orbital on P and the axial and equatorial H 1s orbitals, in which the axial and equatorial components are in opposite phases. The participation of the 3dz2 orbital in particular is evident from the existence of a conical nodal plane separating the axial and equatorial regions. |