Modals15
Ammonia, Nitrogen and Hydrogen
NH3 Molecule
Molecule: NH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
E(RB3LYP): -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3V
Bond Length (N-H): 1.01798 Å
Bond Angle (H-N-H): 105.741°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
NH3 |
The optimisation file is linked here
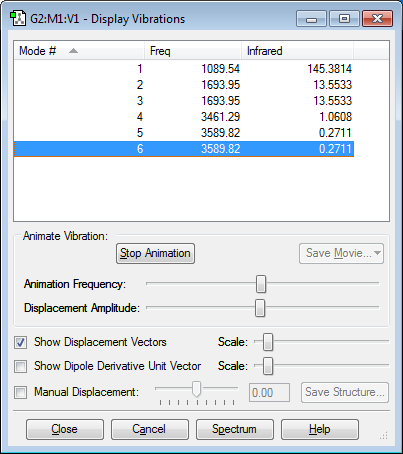
Six modes of vibration are expected from 3N-6 rule.
Modes 2 and 3 are degenerate and modes 5 and 6 are also degenerate because they have the same value for frequency.
Bending vibration modes: 1,2 and 3
Bond stretching modes: 4, 5 and 6
Mode 4 is highly symmetric.
Mode 1 is the umbrella mode.
Two bands are expected to be seen in the spectrum for ammonia because modes 2 and 3 result in one band, modes 5 and 6 would result in one band and mode 1 and mode 4 would result in one band each. However, the intensity of the mode 4 band and the mode (5+6) band are small, so only two bands appear.
Charge on N-atom: -1.125 e
Charge on H-atom: 0.375 e
It is expected that the N-atom would have a negative charge because it is more electronegative than hydrogen. The nitrogen atom would pull the electrons in the N-H bond closer to itself and more electron density would be around the nitrogen atom.
N2 Molecule
Molecule: N2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
E(RB3LYP): -109.52412868 a.u.
RMS Gradient Norm: 0.00000060 a.u.
Point Group: D*H
Bond Length (N-N): 1.10550Å
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
N2 |
The optimisation file is linked here
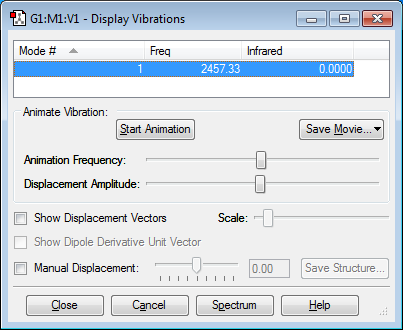
From the 3N-5 rule for linear molecules, 1 mode of vibration was expected. No bands would be seen as the mode of vibration (bond stretching) does not involve a change in dipole moment.
The charge of each N-atom is zero because the difference in electronegativity is zero and, therefore, the electron distribution would be equally distributed over the two atoms.
H2 Molecule
Molecule: H2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
E(RB3LYP): -1.17853936 a.u.
RMS Gradient Norm: 0.00000017 a.u.
Point Group: D*H
Bond Length (H-H): 0.74279Å
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
H2 |
The optimisation file is linked here
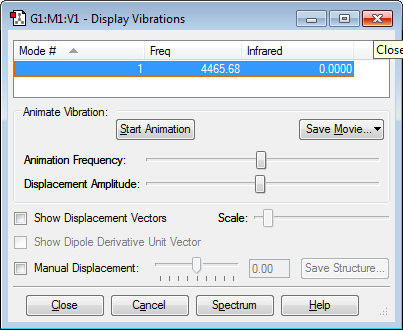
From the 3N-5 rule for linear molecules, 1 mode of vibration was expected. No bands would be seen as the mode of vibration (bond stretching) does not involve a change in dipole moment.
The charge of each H-atom is zero because the difference in electronegativity is zero and, therefore, the electron distribution would be equally distributed over the two atoms.
Haber-Bosch Reaction Energy
N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.1155375 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u.
ΔE= -146.48 kJ mol-1
The ammonia product is more stable than the gaseous reactants as the energy of the right-hand side is lower than that of the left-hand side of the equation.
Project Molecule
Summary
Molecule: H2CO
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
E(RB3LYP): -114.50319933 a.u.
RMS Gradient Norm: 0.00007386 a.u.
Point Group: CS
Bond Length (C-H): 1.11057Å
Bond Length (C=O): 1.20676Å
Bond Angle (H-C=O): 122.395°
Bond Angle (H-C-H): 115.219°
The literature value for C-H bond length is 1.1110Å (higher than expected) and for the C=O bond it is 1.2050Å (lower than expected). The literature value for the H-C=O angle is 121.933° and for the H-C-H angle it is 116.134°.[1]
Item Value Threshold Converged? Maximum Force 0.000197 0.000450 YES RMS Force 0.000085 0.000300 YES Maximum Displacement 0.000270 0.001800 YES RMS Displacement 0.000149 0.001200 YES
H2CO |
The optimisation file is linked here
Frequency Analysis and Charges
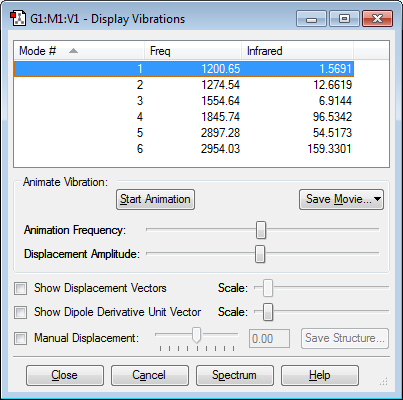
From 3N-6 rule, six modes of vibration are expected.
None of the modes are degenerate.
Bending vibration modes: 1 and 2
Modes involving bending and stretching: 3 and 4
Bond stretching modes: 5 and 6
Five bands are expected because there are six modes corresponding to six different frequencies, but mode 1 has a small intensity so it would not be seen.
Charge on C-atom: 0.221 e
Charge on O-atom: -0.494 e
Charge on H-atom: 0.137 e
The charge on the oxygen is negative because it is a lot more electronegative than the other atoms in the molecule, so the electrons in the molecule will be pulled towards the oxygen atom. The charge on the carbon is more positive than the charge on the hydrogen because it is bonded to the highly electronegative oxygen atom. The oxygen atom attracts the electrons of the C=O bond more strongly than it attracts the electrons of the C-H bond.
Molecular Orbitals
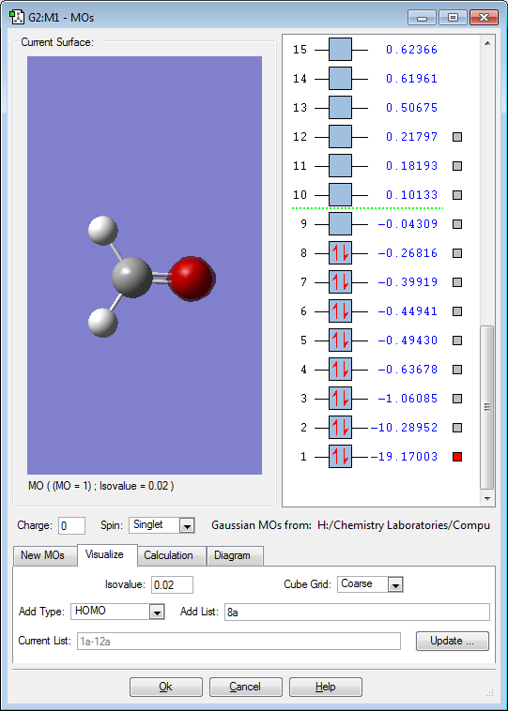
MO 1
MO 1 is a non-bonding 1s orbital of the oxygen atom.
MO 2
MO 1 is a non-bonding 1s orbital of the carbon atom. It is more diffuse than the 1s(O) because carbon is more electropositive, so it would hold the electron less tightly.
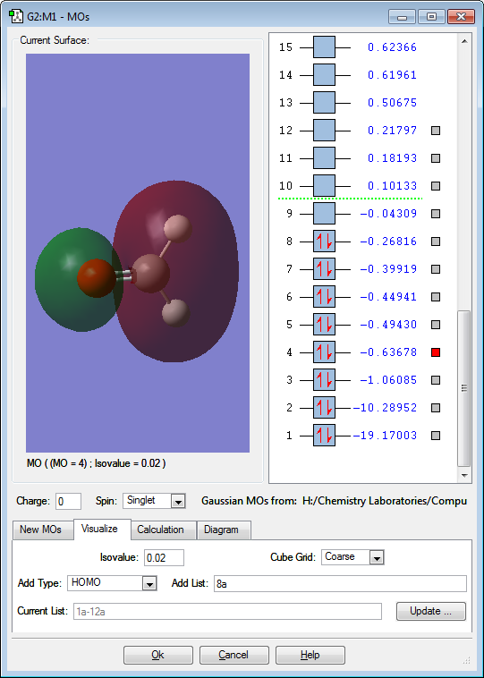
MO 4
MO4 is a sigma anti-bonding orbital which results from the overlapping of a 2s orbital from carbon and a 2s orbital from oxygen, which are out of phase. The MO is filled which cancels out the filled sigma bonding orbital (from the 2s(C)-2s(O) in phase overlap), so no bonding results from the filled sigma bonding orbital. The lobe on the carbon atom is bigger than that on the oxygen atom because carbon is more electropostive so it contributes more to the anti-bonding orbital.
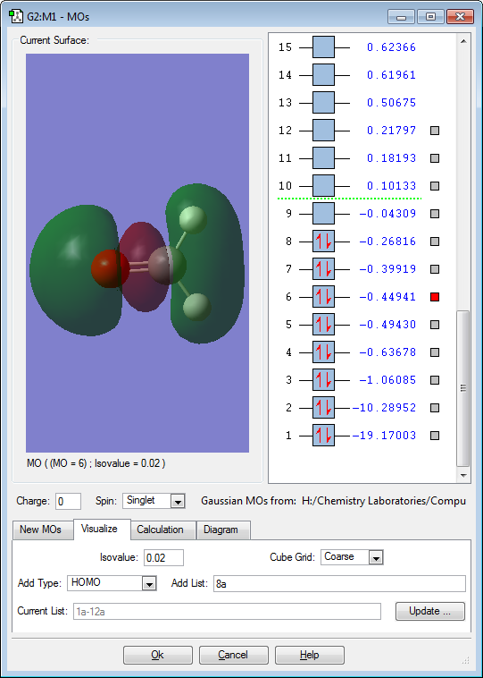
MO 6
MO6 is a sigma bonding orbital resulting from the overlap of a 2px(C) and a 2px(O) which are in the same phase (where x is in the horizontal direction). The red lobe is smaller because the MO has been mixed with the sigma bonding orbital from the 2s(C)-2s(O) overlap. The MO is occupied, which results in a sigma bond because the corresponding sigma anti-bonding orbital is not filled.
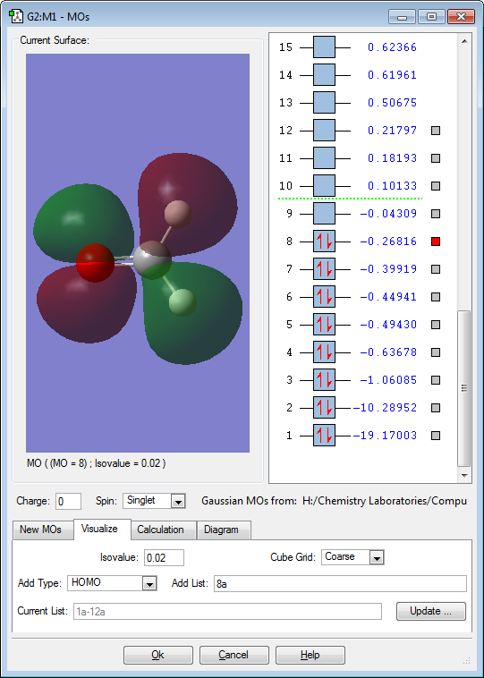
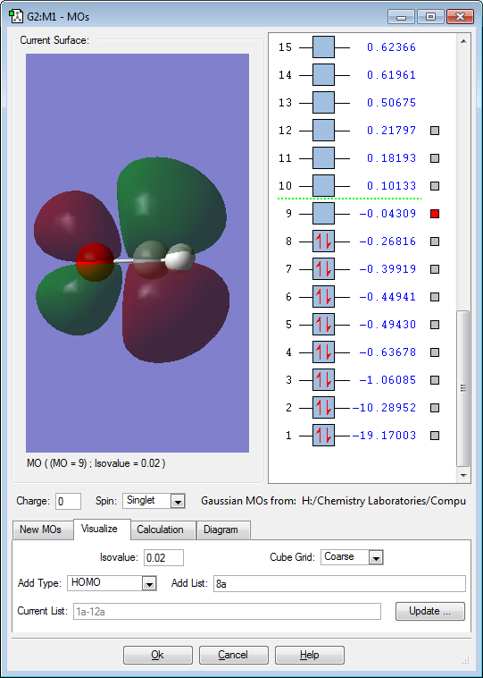
MO 8
MO8 is a pi anti-bonding orbital resulting from the overlap of 2py(C)-2py(O) that are out of phase. The MO is filled and cancels out one of the filled pi bonding orbitals, so that only one pi bond is present. The lobes are bigger on the carbon side because carbon is electropositive and ocntributes more to the anti-bonding orbital.
MO 9
MO9 is a pi anti-bonding orbital resulting from the overlap of 2pz(C)-2pz(O) that are out of phase. It is not filled, so it doesn't cancel out any filled bonding orbitals.
MO8 is the HOMO and MO9 is the LUMO and they are not deep in energy. When the C=O band acts as an electrophile, the LUMO is filled, breaking the pi bond.