Mod GPQ2017
NH3 Molecule

NH3 molecule |
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -56.55776873 au
RMS gradient: 0.00000485 au
Point group: C3V
Optimised N-H bond distance: 1.01798 A
Optimised H-N-H bond angle: 105.741°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
The NH3 optimisation file is linked to here
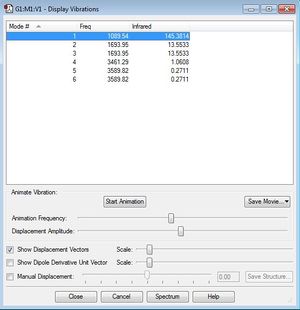
Questions:
6 vibrational modes are expected from the 3N-6 rule. There are 2 pairs of degenerate vibrational modes: 2 and 3, 5 and 6. Modes 1,2 and 3 are bending vibrations. Modes 4,5 and 6 are bond stretch vibrations. Mode 4 is highly symmetric. Mode 1 is known as the umbrella mode. In an experimental spectrum of gaseous ammonia, 4 bands are to be expected. However, it is more likely that only 2 bands will be visible as vibrations 4,5, and 6 are very low in intensity.
Charge Analysis: The charge on the N-atom was found to be -1.125. The charge on the H-atom was found to be 0.375. Nitrogen is the more electronegative element and so we would expect its charge to be negative as it draws electron density towards itself and away from the hydrogens; resulting in positively charged hydrogens.
N2 Molecule
N2 molecule |
Summary Information:
Basis Set: 6-31G(d,p)
Final Energy: -109.52412868 au
RMS Gradient: 0.00000060 au
Point Group: D*H
Optimised N2 bond length: 1.10550 A
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
1 mode of vibration at 2457.33 (non-negative).
The N2 optimisation file is linked to here
H2 Molecule
H2 molecule |
Summary Information:
Basis Set: 6-31G(d,p)
Final Energy: -1.17853936 au
RMS Gradient: 0.00000017 au
Point Group: D*H
Optimised H2 bond length: 0.74279 A
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
1 mode of vibration at 4465.68 (non-negative).
The H2 optimisation file is linked to here
Energy for Haber-Bosch process:
E(NH3)= -56.55776873 au
2*E(NH3)= -113.1155375 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 au
ΔE= -146.4785879 kJ/mol
The ammonia product is more stable than the gaseous reactants; overall the energy change is negative meaning that energy is released in an exothermic reaction resulting in the formation of more stable products.
F2 Molecule
F2 molecule |
Summary Information:
Basis Set: 6-31G(d,p)
Final Energy: -199.49825218 au
RMS Gradient: 0.00007365 au
Point Group: D*H
Optimised F2 bond length: 1.40281 A
1 mode of vibration at 1065.09 (non-negative). This vibration is not IR active as there is no accompanying change in dipole moment upon vibration.
Relative to each other, the fluorine molecules have no charge as they are both equally electronegative. This means that there is a symmetric distribution of charge resulting in the absence of any dipole.
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
The F2 optimisation file is linked to here
F2 Molecular Orbitals:
This molecular orbital represents a bonding situation between two 2s atomic orbitals. The MO encompasses the entire molecule with no nodal planes and hence can be described as bonding. It is low in energy, only above the non-bonding 1s MO. This MO is occupied by an anti-parallel spin electron pair, with one electron coming from each of the fluorine atoms.
This is the anti-bonding 2s MO. One nodal plane (where electron density is zero) is evident as the atomic orbitals that are combining are out of phase. As the MO is anti-bonding, it is higher in energy than the corresponding bonding 2s orbital. It is occupied by an electron pair as it is still lower in energy than the subsequent orbitals.
Two nodal planes are present in this bonding 2p (sigma) MO. These originate from the nodal planes present in the corresponding 2p atomic orbitals. This MO is labelled as 'sigma' as the atomic orbitals combining do so along the axis of the bond, therefore there is no change in sign of the wavefunction upon rotation of the MO about an internuclear axis. It is a bonding situation as the p AOs combine in-phase. This MO also participates in bonding, and is lowest in energy out of the p-orbital combinations.
This MO corresponds to the antibonding 2p (sigma). Three nodal planes are present as the 2p AOs combine out-of-phase and this can be seen by the alternating colours that represent the different phases. This MO is occupied but being antibonding makes it higher in energy than the corresponding bonding MO. It also fills after the other bonding 2p (pi) orbitals as described below.
This is the bonding 2p (pi) MO and 1 nodal plane is present along the axis of the bond. It is the result of two 2p AOs combining but is labelled 'pi' rather than 'sigma' as the wavefunction of the MO changes sign upon a 180° rotation about the internuclear axis. This is because the combing p-orbitals do not combine along the axis of the bond but instead create two regions of electron density above and below the bond. It is one of two degenerate bonding 2p (pi) MOs as there are two sets of p-orbitals that are not orientated parallel to the axis of the bond. It is thus higher in energy than the 2p (sigma) MO and is also involved in bonding.
Additional Analysis
Upon comparison with a literature value, it was found that the enthalpy of formation for the Haber process is -92 kJ/mol [1]. This is significantly less negative than the value calculated earlier (-146 kJ/mol). This is most likely due to the experimental conditions. Typically, the Haber process operates at high temperature (400°C) and high pressure (200atm). Under these conditions, the number of molecular collisions increases, resulting in an increase in internal energy and hence an increase in the enthalpic change.
Cl2 Molecule
An additional calculation was carried out using Cl2 for comparison with the energy of F2.
Summary Information:
Basis Set: 6-31G(d,p)
Final Energy: -920.34987886 au
RMS Gradient: 0.00002510 au
Point Group: D*H
Optimised Cl2 bond length: 2.04174 A
Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000121 0.001800 YES RMS Displacement 0.000172 0.001200 YES
1 mode of vibration at 520.32 (non-negative). This vibration is not IR active as there is no accompanying change in dipole moment upon vibration.
Relative to each other, the chlorine molecules have no charge as they are both equally electronegative. This means that there is a symmetric distribution of charge resulting in the absence of any dipole.
The Cl2 energy is much lower than that of F2. This can be described in terms of repulsion; eventhough the fluorine atoms have a very high effective nuclear charge, they are so small that there is a relatively large amount of internuclear repulsion. This is not the case with Cl2 as the covalent radii is much large and the charge still relatively high. This larger covalent radii is accounted for in the calculation of bond length which is longer than that of F2.
The Cl2 optimisation file is linked to here
References:
1. http://www.chemguide.co.uk/physical/equilibria/haber.html