ModXYZ1234
NH3 molecule
Optimised molecule and method
N-H bond distance = 1.01798 angstrom
H-N-H bond angle = 37.129 degrees
Calculation Type: FREQ
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -56.55776873 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point Group: C3V
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986277D-10
nh3 molecule |
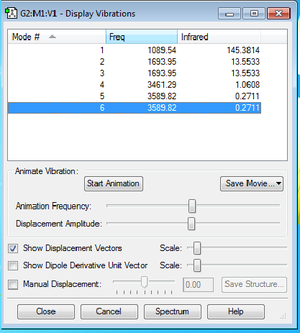
Vibrational mode of NH3
Number of modes using 3N-6 rule: 6 different modes.
Modes that are degenerate: Modes 2 and 3 (same frequency= 1693.95 Hz) and modes 5 and 6 (same frequency= 3589.82 Hz).
Bending modes: 1,2,3 Stretching modes: 4,5,6
Mode 1 is highly symmetrical.
Mode 1 is the umbrella mode.
In the experimental spectrum of gaseous ammonia, we would expect to see 4 bands due to there being 4 frequencies for the 6 modes.
Charge distribution
Charge on nitrogen atom: -1.125 a.u.
Charge on each of the three hydrogen atoms: 0.375 a.u.
The nitrogen is more electronegative than hydrogen so it is expected that a negative charge is present on the nitrogen. As a consequence, a positive charge will be observed on the hydrogen atoms.
N2 Molecule
Optimised molecule and method
Calculation Type: FREQ
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -109.5241286 a.u.
RMS Gradient: Norm 0.00000060 a.u.
Point Group: D*H
n2 molecule |
Vibrational modes and frequency
The N2 frequency is positive and equal to 2457.33 Hz.
H2 Molecule
Optimised molecule and method
Calculation Type: FREQ
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy: -1.17853936 a.u.
RMS Gradient Norm: 0.00000017 a.u.
Point Group: D*H
h2 molecule |
Vibrational modes and frequency
The H2 frequency is positive and equal to 4465.68 Hz.
Haber-Bosch Reaction Energy
N2 + 3h2--> 2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -56.55776873 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u.
ΔE= -0.05579074 x 2625.5 = -146.4785879 kJ/mol.
This value indicates the amount of energy released when nitrogen and hydrogen are converted to ammonia. This shows that ammonia is more stable than a mixture of nitrogen and hydrogen gaseous reactants.
CH4 Molecule
Optimised molecule and method
C-H bond distance= 1.09197 angstrom
H-C-H bond angle= 109.471 degrees
Calculation Type FREQ
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
Final Energy -40.52401404 a.u.
RMS Gradient Norm 0.00003263 a.u.
Point Group TD
Item Value Threshold Converged?
Maximum Force 0.000063 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.000179 0.001800 YES
RMS Displacement 0.000095 0.001200 YES
Predicted change in Energy=-2.256043D-08
Vibrational modes and frequency
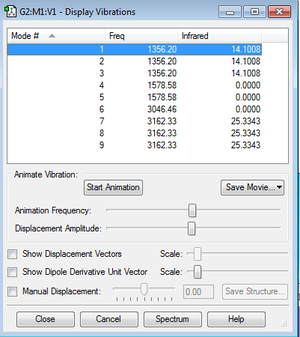
Number of modes using 3N-6 rule: 9 different modes.
Modes that are degenerate: Modes 1,2 and 3 (same frequency= 1356.20 Hz) , modes 4 and 5 (same frequency= 1578.58 Hz) and modes 7,8,9 (same frequency=3162.33).
Bending modes: 1,2,3,4,5 Stretching modes: 6,7,8,9
Modes 4,5 and 6 are highly symmetrical.
In the experimental spectrum of gaseous methane, we would expect to see 4 bands due to there being 4 frequencies for the 9 modes.
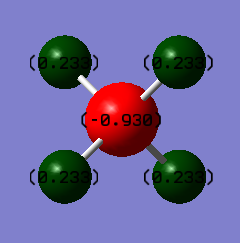
Charge distribution
Charge on carbon atom: -0.930 a.u.
Charge on each of the four hydrogen atom: 0.233 a.u.
The carbon is more electronegative than hydrogen so it is expected that a slightly negative charge is present on the carbon. As a consequence, a very slight positive charge will be observed on the hydrogen atoms
Molecular orbitals

The molecular orbital above represents the 1s electrons in the carbon that are not involved in the bonding of methane. Since these electrons are very close to the carbon atom, they are low in energy so form the most stable molecular orbital.

The bonding orbital above represents the overlap of the 2s of the carbon atom with the 1s electrons in the hydrogen atoms. This is lower in energy than the bonding orbitals below due to the stability of the 2s electrons in carbon.

The bonding orbital above represents the overlap of one of the p orbitals in carbon with the 1s orbitals of the hydrogen atoms. This is highest in energy due to the relatively higher energy of the p orbital used in the overlap.
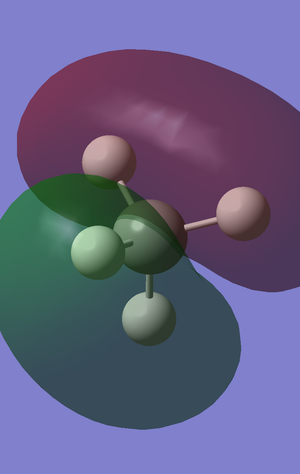
The bonding orbital above represents a similar overlap to that in the diagram above but with a different p orbital of the carbon atom, as well as a different combination of the 1s phases in the hydrogen atom. This is degenerate in energy to the above orbital.

Once again, this represents a similar overlap but formed from the third p orbital of the carbon atom, so has a third distinct orientation. This is also degenerate in energy to the above two orbitals.
One of the three above orbitals represent the HOMO of methane while the LUMO is the anti-bonding orbital formed from the overlap of the 2s orbital in carbon with the 1s orbitals of hydrogen out of phase.