ModTwo:hhlk2010
Borane BH3 Analysis
BH3 |
The structure of molecule BH3 was optimised by the B3LYP method using the basis set of 3-21G. The model of BH3 is shown above.
Geometry Optimisation
| File Type | .log |
| Calculation Type | FOPT |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Final Energy (a.u.) | -26.4622 |
| RMS Gradient Norm (a.u.) | 0.00020672 |
| Dipole Moment (Debye) | 0.00 |
| Point Group | D3h |
| Job Time (s) | 14.00 |
| Optimised B-H Bond length (Å) | 1.19 |
| Optimised B-H Bond Angle ( o) | 120.0 |
Table 1: Optimisation of BH3
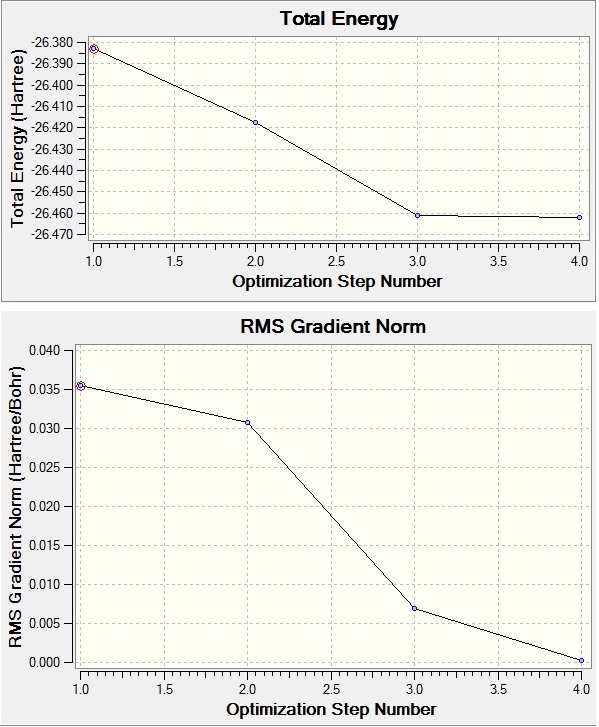
The B-H bond length was set to be 1.50Å before the optimisation. After the optimisation, the bond length of BH3 is 1.19Å and the bond angle between H-B-H is 120o. (see Table 1) BH3 is a trigonal planar with the point group of D3h. The optimisation is converged as the RMS gradient is less than 0.001.(see Table 1)
Molecular Orbitals
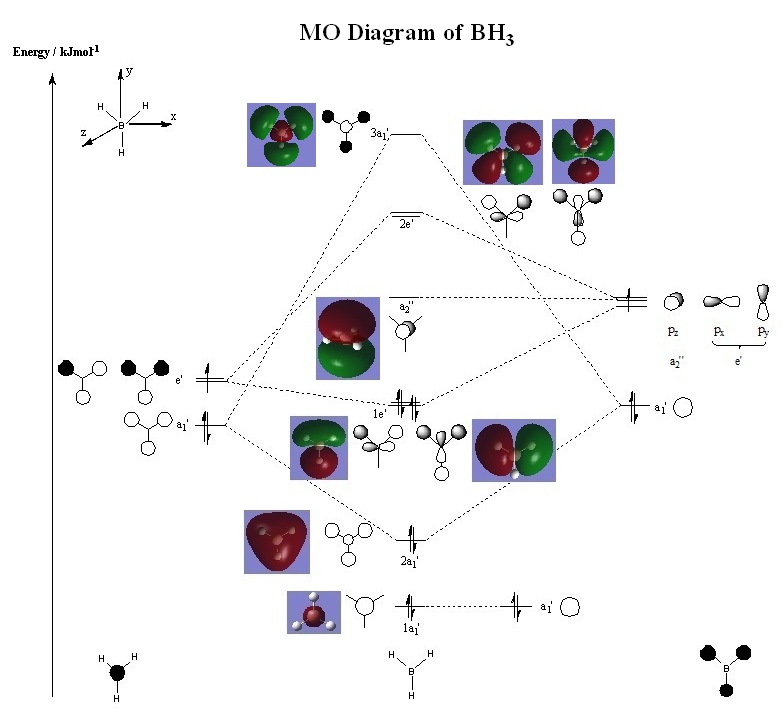
<br\> The Molecular Orbitals of BH3 was computed by Gaussian. The log file of the BH3 analysis can be found at: http://hdl.handle.net/10042/to-5293
A MO Diagram of trigonal planar, (D3h), BH3 [1] using linear combination of atomic orbitals (LCAO) was constructed by ChemDraw and shown above. The atomic orbitals of the same symmetry were mixed to form the molecular orbitals. In the MO Diagram of BH3, the pictures of the MOs from the computational analysis were added in in order to compare with the LCAO MOs. It is seen that there is no significant differences between the shape of the real and LCAO MOs. Nevertheless, the qualitative MO theory cannot predict the MOs precisely. The computational calculations showed that the energy of the 2e' orbital is just slightly lower than that of the 3a1' orbital. However there are actually two possibilities for the energy arrangements. One is the 2e' orbital is in higher energy than 3a1' orbital and the other possibility is the 2e' orbital is in lower energy than 3a1' orbital.
NBO Analysis
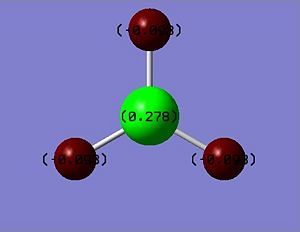
The Natural Bond Orbital (NBO) Analysis of BH3 was computed by gaussian. The NBO results show that there are 3 B-H bonding orbitals. All B-H bonds occupies with 2 electrons. BH3 has sp2 hybridised orbital and bonded with three H atoms. It normally exists as a B2H6 dimer. According to the output file of the NBO calculations, the bonding orbital from B atom is a mixture of 33.33% of s orbital and 66.67% of p orbital. This observation manifests the existence of sp2 hybridised orbitals in BH3.
Summary of Natural Population Analysis
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.27816 1.99954 2.72230 0.00000 4.72184
H 2 -0.09272 0.00000 1.09256 0.00015 1.09272
H 3 -0.09272 0.00000 1.09256 0.00015 1.09272
H 4 -0.09272 0.00000 1.09256 0.00015 1.09272
=======================================================================
* Total * 0.00000 1.99954 6.00000 0.00046 8.00000
The Natural Population Analysis shows the natural charge on each atoms in BH3.
According to the results, the Boron atom has the natural charge of 0.2782 and each H atoms has the natural charge of -0.09272.
Bond orbital/ Coefficients/ Hybrids
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99854) BD ( 1) B 1 - H 2
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 2 s(100.00%)
1.0000 0.0001
2. (1.99854) BD ( 1) B 1 - H 3
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 3 s(100.00%)
1.0000 0.0001
3. (1.99854) BD ( 1) B 1 - H 4
( 45.36%) 0.6735* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 54.64%) 0.7392* H 4 s(100.00%)
1.0000 0.0001
4. (1.99954) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
(...)
The above table indicates the key information about the bonds in BH3. This part of the NBO analysis partitions the electron density of the whole molecule out into atomic like orbitals. For instance, the first bond (BD) is between boron (atom 1) and hydrogen (atom 2). 45.36% of the bond is contributed from the B orbitals which have a hybridisation of 33% s + 66% p, while 54.64% of the bond comes from the H orbital which is 100% s. Therefore the B atoms formed 3 sp3 hybridised orbitals which each interacts with the s atomic orbital of one H atom.
Natural Bond Orbitals (Summary)
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99854 -0.43328
2. BD ( 1) B 1 - H 3 1.99854 -0.43328
3. BD ( 1) B 1 - H 4 1.99854 -0.43328
4. CR ( 1) B 1 1.99954 -6.68393 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.53915
6. RY*( 1) B 1 0.00000 0.37512
7. RY*( 2) B 1 0.00000 0.37512
8. RY*( 3) B 1 0.00000 -0.04064
9. RY*( 4) B 1 0.00000 0.41499
10. RY*( 1) H 2 0.00015 0.73308
11. RY*( 1) H 3 0.00015 0.73308
12. RY*( 1) H 4 0.00015 0.73308
13. BD*( 1) B 1 - H 2 0.00146 0.42130
14. BD*( 1) B 1 - H 3 0.00146 0.42130
15. BD*( 1) B 1 - H 4 0.00146 0.42130
-------------------------------
Total Lewis 7.99516 ( 99.9396%)
Valence non-Lewis 0.00437 ( 0.0547%)
Rydberg non-Lewis 0.00046 ( 0.0058%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
This section are recorded the energy and population or occupation of the B-H bonds and the boron lone pair (LP*). This NBO summary section indicates that molecular 8 is the unoccupied MO with the lowest energy of -0.041 Hartree a.u., which is also known as LUMO. This is the empty p orbital on B atom. The negative energy shows that BH3 is extremely reactive as the empty p orbital makes the BH3 behaves like a Lewis acid as it is desperate to accept electrons in order to reach the even more stable state.
Frequencies and Vibrations
| Number | Image | Form of Vibration | Calculated Frequency/cm-1 | Literature Frequency[2]/cm-1 | Intensity | Symmetry (D3h Point Group) |
| 1 |  |
All H atoms move in and out of the BH3 plane in a same motion, the B atom moves in an opposite direction at a smaller amplitude. | 1144 | 1159 | 93 | a2" |
|---|---|---|---|---|---|---|
| 2 |  |
2 H atoms move towards and away from each other in a same motion, the other H atom and the B atom are stationary. | 1204 | 1202 | 12 | e' |
| 3 |  |
3 B-H bonds bend and the B atom is stationary. | 1204 | 1202 | 12 | e' |
| 4 |  |
All B-H bonds stretches symmetrically while the B atom is stationary. | 2598 | / | 0 | a1' |
| 5 |  |
One H atom and the B atom are stationary, the other two B-H bonds stretch asymmetrically. | 2737 | 2506 | 104 | e' |
| 6 |  |
2 H atoms move towards and away from the B atom in the BH3 plane in a same motion, while the other H atom vibrates out-of-phase and the B atom is stationary. | 2737 | 2616 | 104 | e' |
Table 2: Vibrational Frequencies of BH3

The Frequency Analysis was calculated in Gaussview to determine the optimised structure of BH3. This analysis can also predicts the molecular vibrational frequencies which correspond to the IR spectrum of the molecule. Table 2 shows the Vibrational Frequencies of BH3. There are 6 BH3 molecular vibrations where only 3 peaks are visible in the IR spectrum. This is because the 6 vibrations only have 4 different frequencies and one of these intensities is zero. The zero intensity is due to no change in dipole moment during the vibration. Furthermore there are two degeneracy pairs which are at 1204 cm-1 and 2737 cm-1 show up only once in the IR spectrum. The calculated frequencies are not perfectly matched with the literature values, which means the calculations used are not perfect.
TlBr3 Analysis
Geometry Optimisation
BH3 |
TlBr3 is a trigonal planar with a point group of D3h. The optimisation of TlBr3 was conducted in Gassview. The method of calculation is DFT-B3LYP and the basis set is LANL2DZ. The TlBr3 optimisation file can be found at: http://hdl.handle.net/10042/to-5388
| File Type | .log |
| Calculation Type | FOPT |
|---|---|
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Final Energy (a.u.) | -91.2181 |
| RMS Gradient Norm (a.u.) | 0.00000090 |
| Dipole Moment (Debye) | 0.00 |
| Point Group | D3h |
| Job Time (s) | 17.30 |
| Optimised B-H Bond length (Å) | 2.65 |
| Optimised B-H Bond Angle ( o) | 120.0 |
Table 3: Optimisation of TlBr3
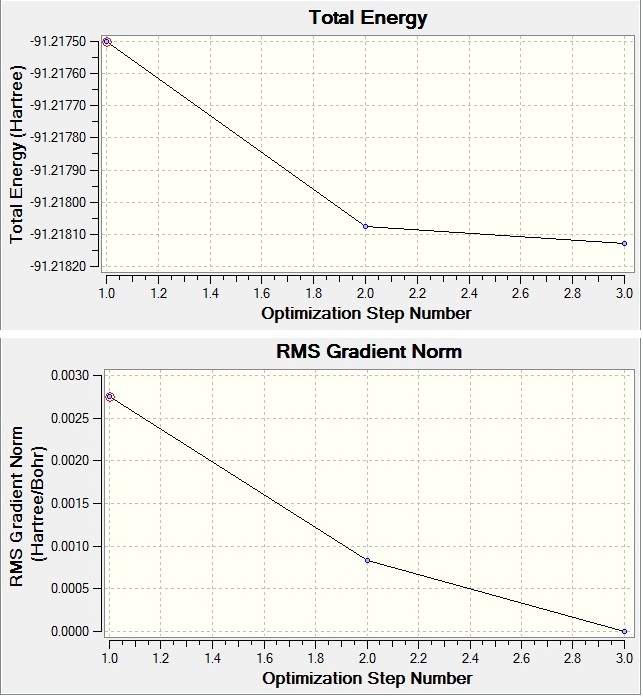
The optimisation file shows that TlBr3 has a D3h symmetry as expected for its trigonal planar geometry. The bond angle is 120o and the bond length of Tl-Br is 2.65 Å (see Table 3) which correspond to the literature values[3] (bond angle: 120o; bond length: 2.51 Å). The RMS Gradient Norm is 0.00000090 a.u. (see Table 3) which is less than 0.001 a.u.. This result of RMS Gradient Norm ensures the optimisation of TlBr3 is completed.
Discussion on Chemical Bonds
A chemical bond is an attraction between two or more atoms that allows the formation of chemical compounds. A chemical bond is the attraction caused by the electromagnetic interaction between positively charged nuclei and negatively charged shared electrons. Covalent or ionic bonds[4] are defined as strong bonds and the dipole-dipole interactions or hydrogen bonding are defined as weak bonds.
Some of the bonds in a structure cannot be shown in Gaussview. This is not because the bonds between the atoms do not exist. This is caused by the programming restraints. As Gaussview has its own database of bond lengths which directs the program when to draw a bond between atoms, the calculated bond length cannot be shown if it exceeds the specified bond lengths range in the database. This usually happens for inorganic compounds since the bond lengths in the database are mainly based on organic compounds.
Frequencies and Vibrations
| Number | Image | Form of Vibration | Calculated Frequency/cm-1 | Literature Frequency[3]/cm-1 | Intensity | Symmetry (D3h Point Group) |
| 1 |  |
2 Br atoms move towards and away from each other in a same motion, the other Br atom and the Tl atom are stationary. | 46 | / | 4 | e' |
|---|---|---|---|---|---|---|
| 2 |  |
The Tl atom is stationary and the Tl-Br bonds bend. | 46 | / | 4 | e' |
| 3 |  |
All Br atoms move in and out of the TlBr3 plane in a same motion, the Tl atom moves in an opposite direction at a smaller amplitude. | 52 | / | 6 | a2" |
| 4 |  |
All Tl-Br bonds stretches symmetrically while the Tl atom is stationary. | 165 | 190 | 0 | a1' |
| 5 |  |
Two Tl-Br bonds stretch asymmetrically, the Tl atom moves towards and away from the centre to the left side. | 211 | 202 | 25 | e' |
| 6 |  |
2 Br atoms move towards and away from the Tl atom in the TlBr3 plane in a same motion, while the other Br atom vibrates out-of-phase and the Tl atom is stationary. | 211 | 202 | 25 | e' |
Table 4: Vibrational Frequencies of TlBr3
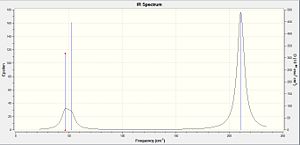
The Frequency Analysis was calculated in Gaussview to determine the optimised structure of TlBr3. This analysis can also predicts the molecular vibrational frequencies which correspond to the IR spectrum of the molecule. Table 4 shows the Vibrational Frequencies of TlBr3. The TlBr3 frequency file can be found at: http://hdl.handle.net/10042/to-5389. There are 6 TlBr3 molecular vibrations where only 3 peaks are visible in the IR spectrum. This is because the 6 vibrations only have 4 different frequencies and one of these intensities is zero. The zero intensity is due to no change in dipole moment during the vibration. Furthermore there are two degeneracy pairs which are at 46 cm-1 and 211 cm-1 show up only once in the IR spectrum. The calculated frequencies are not perfectly matched with the literature values, which means the calculations used are not perfect. But the trends of the calculated and literature frequencies are the same which indicate the results are still reliable, the structure which was examined in the IR analysis is the correct structure of TlBr3.
Isomers of Mo(CO)4L2 Analysis
The structures of cis- and trans- isomers of Mo(CO)4(PCl3)2 were optimised by Gaussview using DFT method with the basis set of LANL2DZ. Using LANL2DZ as the basis set instead of 6-311G mainly because it is a high accurate pseudo-potential with tight convergence. Furthermore all elements with larger atomic number than Zn cannot not be recognised by the 6-311G basis set too. The comparison of the energies and IR spectra of the isomers were conducted in this analysis.
Geometry Optimisation
| Property | Cis-Mo(CO)4(PCl3)2 | Trans-Mo(CO)4(PCl3)2 | ||||||
| Molecule |
|
| ||||||
|---|---|---|---|---|---|---|---|---|
| File Type | .log | .log | ||||||
| Calculation Type | FOPT | FOPT | ||||||
| Calculation Method | RB3LYP | RB3LYP | ||||||
| Basis Set | LANL2DZ | LANL2DZ | ||||||
| Final Energy (a.u.) | -623.5768 | -623.5759 | ||||||
| RMS Gradient Norm (a.u.) | 0.00008645 | 0.00001236 | ||||||
| Dipole Moment (Debye) | 1.2270 | 0.0000 | ||||||
| Job Time | 59 mins 41.9 s | 25 mins 24 s |
Table 5: Geometry Optimisations of cis- and trans- isomers of Mo(CO)4(PCl3)2
The log files of the Geometry Optimisations of cis- and trans- isomers of Mo(CO)4(PCl3)2 can be found in the following links:
Cis-Mo(CO)4(PCl3)2: http://hdl.handle.net/10042/to-5510
Trans-Mo(CO)4(PCl3)2: http://hdl.handle.net/10042/to-5479
According to Table 5, the cis-isomer is lower in energy than the trans-isomer. This is due to a stalemate between electronic and steric factors. Electronically, trans effect in the Mo complex favours the cis-isomer. Since the CO ligands are strong pi-acceptors and have a very strong trans effect, the preferred orientation of the ligands is that there are less CO ligands opposite to each other. The optimisations are converged as the RMS gradients are both less than 0.001.(see Table 5)
Frequencies and Vibrations
The log files of the Vibrational Frequencies of cis- and trans- isomers of Mo(CO)4(PCl3)2 can be found in the following links:
Cis-Mo(CO)4(PCl3)2: http://hdl.handle.net/10042/to-5491
Trans-Mo(CO)4(PCl3)2: http://hdl.handle.net/10042/to-5492
| Molecule | Image | Calculated Frequency/cm-1 | Intensity |
| Cis |  |
23.88 | 0.0092 |
|---|---|---|---|
| Cis |  |
45.57 | 0.1120 |
| Cis |  |
46.96 | 0.0237 |
| Trans |  |
2.72 | 0.0000 |
| Trans |  |
37.90 | 0.4011 |
| Trans | 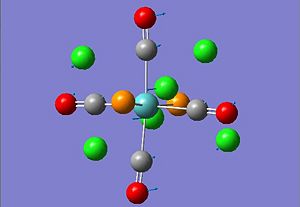 |
38.58 | 0.3750 |
Table 6: Low-Frequency Vibrations of cis- and trans- isomers of Mo(CO)4(PCl3)2
Both cis- and trans- isomers molecules in the low frequency vibrations behave like a continuous elastic body.[5] These vibrations require small amount of energy to occur since energy is directly proportional to frequency. The complex receives enough energy at room temperature for the ground state vibrational levels to be depopulated.
Moreover, these low vibrational frequencies are anharmonic and contibute to the entropy of the system which result in temperature-dependence of the vibrational frequencies. These vibrations are asymmetric owing to the thermal excitation.
| Calculated Frequency/cm-1 | Literature Frequency[6]/cm-1 | Intensity | Symmetry (C2v Point Group)[6] |
| 1944 | 1986 | 767 | B2 |
| 1949 | 1994 | 1489 | B1 |
| 1958 | 2004 | 651 | A1 |
| 2023 | 2072 | 567 | A1 |
Table 7: Carbonyl Stretching Frequencies of cis-Mo(CO)4(PCl3)2
| Calculated Frequency/cm-1 | Literature Frequency[6]/cm-1 | Intensity | Symmetry (D4h Point Group)[6] |
| 1950 | 1896 | 1470 | Eu |
| 1951 | 1896 | 1469 | Eu |
| 1977 | / | 0.00 | B1g |
| 2031 | / | 0.00 | A1g |
Table 8: Carbonyl Stretching Frequencies of trans-Mo(CO)4(PCl3)2

Both cis- and trans- isomers of Mo(CO)4(PCl3)2 were computed to obtain the carbonyl stretching frequencies. The position of the PCl3 groups strongly affect the CO bond strength and its stretching frequencies since PCl3 is a pi-acceptor ligand.[7] The calculated CO stretching frequencies for both cis- and trans- isomers of Mo(CO)4(PCl3)2 are compared with the literature values in Table 7 & 8.
For Cis-Mo(CO)4(PCl3)2, there is no symmetric CO stretch in the molecule as the CO groups are not symmetrically arranged around the Mo centre. Thus all CO stretches are IR active. Nonetheless, the calculated frequencies are poor match to the literature values. This is because Gaussian does not include the pi-backbonding of the CO ligand into the calculation.
For Trans-Mo(CO)4(PCl3)2, the CO stretches at 1977 and 2031 cm-1 have no intensities. Hence no observations in the IR spectrum. This can be explained by the fact that the symmetric CO stretches in the trans-isomer result in no change in net dipole moment, therefore they are IR inactive.[8] The calculated frequencies are poor match to the literature values. This is because Gaussian does not include the pi-backbonding of the CO ligand into the calculation.
Mini Project: Borazine and Borazine Analogues (Al3N3H6 and Al3P3H6)
Introduction
Borazine and its two analogues (Al3N3H6 and Al3P3H6) were examined and compared in this project. All structures was first optimised using Gaussview and their data analyses were computed by the HPC server. Structures were optimised with the DFT:B3LYP method and 6-311G(d,p) was used as the basis set. All calculations were performed with this method and basis set in this project. The aim of this project is to compare these molecules by observing the structures, energies, NBO charge distribution and molecular orbitals, also to see if the geometry of Borazine analogue: Al3P3H6 is planar or bent. Thus the discussion was substantially splitted into three parts: Structural Optimisations, Molecular Orbitals and NBO Charges Distribution.
Structural Analysis
| Property | Borazine | Borazine Analogue: Al3N3H6 | Borazine Analogue: Al3P3H6 | |||||||||
| Molecule |
|
|
| |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| File Type | .log | .log | .log | |||||||||
| Calculation Type | FOPT | FOPT | FOPT | |||||||||
| Calculation Method | RB3LYP | RB3LYP | RB3LYP | |||||||||
| Basis Set | 6-311G(d,p) | 6-311G(d,p) | 6-311G(d,p) | |||||||||
| Final Energy (a.u.) | -242.7445 | -895.5009 | -1755.2004 | |||||||||
| RMS Gradient Norm (a.u.) | 0.00007130 | 0.00006638 | 0.00001102 | |||||||||
| Dipole Moment (Debye) | 0.0003 | 0.0015 | 0.8232 | |||||||||
| Job Time | 6 mins 51.3 s | 12 mins 38.9 s | 15 mins 56.0 s | |||||||||
| Optimised B-H Bond length (Å) | 1.19 | / | / | |||||||||
| Optimised B-N Bond length (Å) | 1.43 | / | / | |||||||||
| Optimised N-H Bond length (Å) | 1.01 | 1.01 | / | |||||||||
| Optimised Al-N Bond length (Å) | / | 1.80 | / | |||||||||
| Optimised Al-H Bond length (Å) | / | 1.58 | 1.58 | |||||||||
| Optimised Al-P Bond length (Å) | / | / | 2.30 | |||||||||
| Optimised P-H Bond length (Å) | / | / | 1.42 |
Table 9: Geometry Optimisations of Borazine and its two analogues
The log files of the Geometry Optimisations of Borazine and its two analogues can be found in the following links:
Borazine: http://hdl.handle.net/10042/to-5446
Borazine Analogue: Al3N3H6: http://hdl.handle.net/10042/to-5447
Borazine Analogue: Al3P3H6: http://hdl.handle.net/10042/to-5448
Borazine was first prepared by Stock and Pohland in 1923.[9] It is a compound isoelectronic to benzene which is so-called an 'inorganic benzene'. Similar to benzene, it is a 6 pi-electrons, 6 membered ring which exhibits cyclic delocalisation. However its delocalisation is not as great as in benzene owing to the difference in electronegativity between B and N atoms, compared to the C atoms in benzene ring which are all the same. All the atoms is planar in borazine (see the molecular model in Table 9) which suggests a large degree of delocalisation of electron density above and below the ring. The B-N bond length is 1.43Å, the B-H bond length is 1.19Å and the N-H bond length is 1.01Å which all correspond to their literature values[10] (B-N bond length: 1.44Å; B-H bond length: 1.26B-HÅ; N-H bond length: 1.05Å) The optimisation is converged as the RMS gradient is less than 0.001.(see Table 9)
In Borazine Analogue: Al3N3H6, the N-H bond length is 1.01Å which is exactly the same as the N-H bond length in borazine. The Al-N bond length is 1.80Å, which is longer than the B-N bond in borazine. In general, the size of the atom increases, the X-Y distances tend to increase. (X is the atoms in group 13 and Y is the atoms in group 15) As the size of Al atom is larger and B is more electronegative compared with Al, which then pulls the N atom closer, thus the bond distance of Al-N is increased. Furthermore the Al-H bond length is 1.58Å, which is also longer than the B-H bond in borazine. This is owing to the higher electronegativity of B atoms too. This borazine analogue is still a 6 pi-electrons, 6-membered ring which exhibits cyclic delocalisation. Nevertheless its delocalisation is less than in borazine as there is larger difference in electronegativity between Al and N atoms. As the electronegativity difference between the X-Y pairs increases, the aromatic stabilisation decreases.[11] The optimisation is converged as the RMS gradient is less than 0.001.(see Table 9) And the structure of this molecule is correctly optimised as its Al-N bond length and Final Energy (1.80Å; -895.5009 a.u.) correspond to the literature values[11] (1.80Å; -895.3757 a.u.).
In Borazine Analogue: Al3P3H6, the Al-H bond length is 1.58Å which is exactly the same as the Al-H bond length in Al3N3H6. The Al-P bond length is 2.30Å, which is longer than the Al-N bond in Al3N3H6. As the size of P atom is larger than N atom, thus the bond distance is increased. Furthermore the P-H bond length is 1.42Å, which is also longer than the N-H bond in Al3N3H6. This is because N is more electronegative compared with P, which then pulls the hydrogen atom closer, thus the bond distance of P-H is increased. This borazine analogue is still a 6 pi-electrons, 6-membered ring which exhibits cyclic delocalisation. Nonetheless its delocalisation is the lowest one in these three molecules as there is the largest difference in electronegativity between Al and P atoms. As the electronegativity difference between the X-Y pairs increases, the aromatic stabilisation decreases.[11] The optimisation is converged as the RMS gradient is less than 0.001.(see Table 9) And the structure of this molecule is correctly optimised as its Al-P bond length and Final Energy (2.30Å; -1755.2004 a.u.) correspond to the literature values[11] (2.27Å; -1775.0624 a.u.).
<br\>
Planarity vs Nonplanarity
All the structures were optimised without any symmetry constraints (C1 symmetry). In agreement with the observed planar geometry of borazine and Borazine Analogue: Al3N3H6, the C1 symmetry structure is energetically and structurally very close to the planar optimised geometry. However the nonplanar structure is calculated to be 5 kcal/mol lower in energy than the planar one.[12]
The Borazine Analogue: Al3P3H6 has a boat conformation with average Al-P distance of 2.30Å.(see Table 9) The nonplanarity is owing to the small aromatic stabilisation energy of P and the large inversion barriers of PH3.[11]. The inversion barrier for NH3 is very small compared to those for other group members. Thus all the nitrogen compounds are planar where the other structures, like phosphorus compounds are puckered.
Molecular Orbitals
| Molecule | HOMO - 4 | HOMO - 3 | HOMO - 2 | HOMO - 1 | HOMO | LUMO | LUMO +1 | LUMO +2 | LUMO +3 | LUMO +4 |
| Borazine |  |
 |
 |
 |
 |
 |
 |
 |
 |

|
|---|---|---|---|---|---|---|---|---|---|---|
| Borazine Analogue: Al3N3H6 |  |
 |
 |
 |
 |
 |
 |
 |
 |

|
| Borazine Analogue: Al3P3H6 |  |
 |
 |
 |
 |
 |
 |
 |
 |

|
Table 10: Molecular Orbitals of Borazine and its two analogues
The log files of the Molecular Orbitals of Borazine and its two analogues can be found in the following links:
Borazine: http://hdl.handle.net/10042/to-5449
Borazine Analogue: Al3N3H6: http://hdl.handle.net/10042/to-5450
Borazine Analogue: Al3P3H6: http://hdl.handle.net/10042/to-5451
Table 10 indicates the Molecular Orbitals of Borazine and its two analogues. The results provide some interesting information about these molecules. In borazine, there are delocalised pi clouds in the ring which brings great stability to the molecule. The pi-delocalisation is best visualised in the HOMO-4, HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 orbitals which clearly see the circular patterns of electron density. In Al3N3H6, it also has delocalised pi clouds in the ring. However it is less aromatic than borazine as there are less pi-delocalisation in the ring. Its pi-delocalisation is best visualised in the HOMO-2, HOMO-1, HOMO, LUMO and LUMO+2 orbitals. In Al3P3H6, it is nonplanar in structure which has the lowest pi-delocalisation. Its pi-delocalisation is best visualised in the LUMO+1 and LUMO+2 orbitals only. This results also prove that Al3P3H6 is the least aromatic amongst these three molecules and has the smallest pi-delocalisation.
NBO Charges Distribution
| Molecule | Charge Distribution | Colour Coded
Charge Distribution |
| Borazine |  |

|
|---|---|---|
| Borazine Analogue: Al3N3H6 |  |

|
| Borazine Analogue: Al3P3H6 | 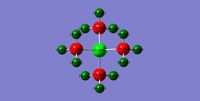 |
|
Table 11: Charge Distributions of Borazine and its two analogues
| Borazine | Borazine | Borazine | Borazine Analogue: Al3N3H6 | Borazine Analogue: Al3N3H6 | Borazine Analogue: Al3N3H6 | Borazine Analogue: Al3P3H6 | Borazine Analogue: Al3P3H6 | Borazine Analogue: Al3P3H6 |
| Bond | Atomic Contribution |
Orbital Contribution |
Bond | Atomic Contribution |
Orbital Contribution |
Bond | Atomic Contribution |
Orbital Contribution |
| B-N | 75.74% from N; 24.26% from B | N:38.89%(s), 61.08%(p), 0.03%(d); B: 31.72%(s), 68.15%(p), 0.14%(d) |
Al-N | 11.95% from Al; 88.05% from N | Al:33.25%(s), 65.53%(p), 0.04%(d);<br\>N: 38.89%(s), 61.09%(p), 0.02%(d) | Al-P | 26.88% from Al; 73.12% from P | Al: 30.95%(s), 68.28%(p), 0.77%(d); P: 18.95%(s), 80.86%(p), 0.20%(d) |
| B-H | 54.77% from H; 45.23% from B | H:99.92%(s), 0.08%(p); B: 36.64%(s), 63.32%(p), 0.04%(d) |
Al-H | 29.22% from Al; 70.78% from H | Al:33.31%(s), 65.96%(p), 0.02%(d); H: 99.90%(s), 0.10%(p) |
Al-H | 32.84% from Al; 67.16% from H | Al: 36.80%(s), 62.69%(p), 0.51%(d); H: 99.87%(s), 0.13%(p) |
| N-H | 29.86% from H; 70.14% from N | H:99.94%(s), 0.06%(p); N: 22.10%(s), 77.85%(p), 0.05%(d) |
N-H | 29.90% from H; 70.10% from N | H:99.96%(s), 0.04%(p); N: 22.07%(s), 77.86%(p), 0.07%(d) |
P-H | 53.23% from P; 46.77% from H | P: 18.70%(s), 80.87%(p), 0.43%(d); H: 99.77%(s), 0.23%(p) |
Table 12: NBO Analysis of Borazine and its two analogues
The log files of the NBO Charge Distributions of Borazine and its two analogues can be found in the following links:
Borazine: http://hdl.handle.net/10042/to-5449
Borazine Analogue: Al3N3H6: http://hdl.handle.net/10042/to-5450
Borazine Analogue: Al3P3H6: http://hdl.handle.net/10042/to-5451
Table 12 shows the results of the NBO Analysis of Borazine and its two analogues. Since these molecules are not isomers and contain different atoms, the energies cannot be compared with great certainty. Generally, all three molecules have very low d orbital contibution. There are pi interactions in all molecules. Al3P3H6 exhibits the smallest pi interaction as its aromatic stabilisation energy is very small and it is nonplanar in structure.
References
- ↑ P. Hunt, The MO diagram of trigonal planar BH3; Imperial College London, 2009
- ↑ M.S. Schuurman, W.D. Allen, H.F. Schaefer III, J. Comput. Chem., 2005, 26, 1106: DOI:10.1002/jcc.20238
- ↑ 3.0 3.1 Hamid Reza Asadi, Mikhail Maliarik, Andrey Ilyukhin and Elena Murashova, Inorganica Chimica Acta, 2009, 362, 2293-2298: DOI:10.1016/j.ica.2008.10.028
- ↑ G.N. Lewis, J. Am. Chem. Soc., 1916, 38, 762: DOI:10.1021/ja02261a002
- ↑ N. Gö, T. Noguti, T. Nishikawa, Appl. Phys. Lett., 2003, 82, 3696: DOI:10.1073/pnas.80.12.3696
- ↑ 6.0 6.1 6.2 6.3 F.A. Cotton, Inorg. Chem., 1964, 3, 702: DOI:10.1021/ic50015a024
- ↑ E.C. Alyea, S. Song, Inorg. Chem., 1995, 34, 3864: DOI:10.1021/ic00119a006
- ↑ S.F.A. Kettle, Symmetry and structure: readable group theory for chemists, 3rd ed., John Wiley and Sons, 2007, pp.105.
- ↑ Stock, A.; Pohland, E. Chem. Ber. 1923, 56, 789.
- ↑ William Harshbarger, George H. Lee II, Richard Francis Porter, Simon Harvey Bauer, Inorg. Chem., 1969, 8(8), 1683–1689: DOI:10.1021/ic50078a023
- ↑ 11.0 11.1 11.2 11.3 11.4 Eluvathingal D. Jemmis and Boggavarapu Kiran, Inorg. Chem., 1998, 37(9), 2110–2116: DOI:10.1021/ic970737y
- ↑ Fink, W. H.n and Richards, J. C. J., Am. Chem. Soc., 1991, 113, 3393
