ModT2:nk6950
Molecular Modelling 2
Ammonia
Ammonia, NH3, when modelled via the B3LYP calculation method using the basis set 6-31G(d,p) and the OPTF function (optimise and frequency analysis) produces the following results:
Final energy E(RB3LYP) in atomic units (au): -56.55776873
RMS gradient: 0.00000485
Point group: C3v
The relative charge on the nitrogen= -1.125 compared to +0.375 on the hydrogens. This is as expected as nitrogen is more electronegative then hydrogen so withdraws electron density inducing a negative charge.
N-H Bond Length: 1.01798Å (Compared to a literature value of 1.012Å) [1]
H-N-H Bond Angle: 105.741° (Compared to a literature value of 106.7°) [1]
The table below is part of the output of the optimization it shows that the forces have converged. As force is the gradient or slope of the energy vs distance graph, and the minimum is where the slope is zero. A system is in equilibrium when there are no net forces acting on it, when the net forces are zero. Therefore when the net force or slope is zero the calculation is finished. The computer never gets to exactly zero because of rounding errors, so aa threshold is applied. The table shows the calculation has finished properly.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy= -5.986311D-10
Ammonia |
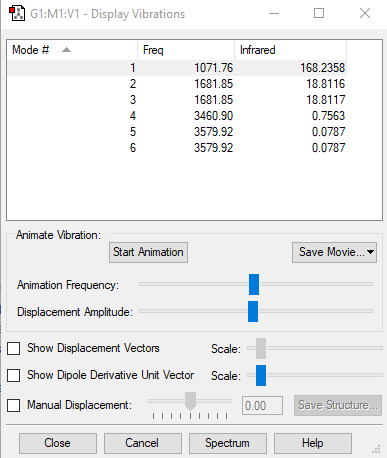
The expected vibrational frequencies of ammonia are as follows 3444, 3337, 1627, 950 cm-1 [2]. A general rule says that a molecule of N atoms will have 3N-6 modes of vibration, hence for ammonia 6 modes of vibration are expected. The image below shows the calculated vibrations.
The vibrational modes 2 and 3 are degenerate as well as 5 and 6. The modes 1, 2 and 3 are 'bending' vibrations, 4, 5 and 6 are 'bond stretch' vibrations. The 6th mode is symmetric. The 1st mode is known as the 'umbrella' mode, as the motion of the hydrogens around the nitrogen looks similar to that of opening and closing an umbrella. In an experimental spectrum of gaseous ammonia four bands would be seen due to the degeneracy of some of the modes.
The enthalpy of formation of ammonia can be calculated in the following way:
E(NH3)=-56.55776873 a.u.
2*E(NH3)=-113.11553746 a.u.
E(N2)=-109.5404119 a.u.
E(H2)=-1.17853936 a.u.
3*E(H2)=-3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.03950748 a.u.
ΔE=-103.72688874 kJ
Therefore the calculated enthalpy of formation of ammonia is: -51.86kJ mol-1 as compared to a literature value of -45.93 kJ mol-1 [3]
Nitrogen
The same modelling method was used for a nitrogen molecule, the results are printed below:
Point Group = D∞h
E(RB3LYP) = -109.52404119 a.u.
Bond length = 1.10550Å (compared to a literature value of 1.10Å) [4]
Stretching Frequency = 2457.33cm-1 (compared to a literature value of 2744cm-1) [5]
The stretching frequency is immeasurable by IR spectroscopy as nitrogen is a homonuclear diatomic molecule.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-1.075999D-15
Nitrogen |
The molecular orbitals can be visualised, images of some of the aforementioned orbitals are printed below. The red box indicates which orbital is being displayed and the numbers refer to the orbitals energy in atomic units.
Hydrogen
The same modelling method was used for a hydrogen molecule, the results are printed below:
Point Group = D∞h
Bond Length= 0.74279Å (compared to a literature value of 0.74Å) [6]
Stretching Frequency=4465.75cm-1 (compared to a literature value of 4342cm-1) [5]
The stretching frequency is immeasurable by IR spectroscopy as hydrogen is a homonuclear diatomic molecule.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000005 0.001800 YES RMS Displacement 0.000007 0.001200 YES Predicted change in Energy=-1.634290D-11
Hydrogen |
Fluorine
Fluorine, F2, when modelled via the B3LYP calculation method using the basis set 6-31G(d,p) and the OPTF function (optimise and frequency analysis) produces the following results:
Point Group = D∞h
Bond length = 1.40Å (compared to a literature value of 1.42Å) [4]
Stretching Frequency = 1065cm-1 (compared to a literature value of 1365cm-1) [5]
E(RB3LYP) = -199.49825220 a.u.
RMS Gradient Norm = 0.00000046 a.u.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000001 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-7.876711D-13
A graph showing how the optimisation took place is pictured below:
The molecular orbitals of fluorine are shown below:
 |
 |
 |
 |
 |

The diagrams show 5 different filled molecular orbital shapes in fluorine, there are also other orbitals. Some of the other orbitals are degenerate to the orbitals shown as they have the same energy and shape, e.g. 8 & 9. By looking at a molecular orbital diagram like the one shown, it can be seen which atomic orbitals make up the molecular orbitals and which diagram they correspond to. Molecular Orbitals 8 & 9 refer to the π*2px/y anti-bonding orbitals, made from the 2p orbitals. The 6th & 7th orbitals are the π2px/y bonding orbitals from the 2p orbitals. Orbital 5 is the σ2pz bonding orbital made from 2p orbitals. Orbitals 3 and 4 are the σ2s and σ*2s bonding and anti bonding orbitals made from 2s orbitals. It can be seen that the high energy π* molecular orbitals will have a large effect on weakening the F-F bond and hence contribute to fluorines strong reactivity (ground state destabilisation) [8]. The diagrams show this as in molecular orbital 9 most of the electron density is pointed away from the bond.
Fluorine |
Bibliography
[1] CRC Handbook of Chemistry and Physics, 94th ed. (http://www.hbcpnetbase.com) [2] http://webbook.nist.gov/cgi/cbook.cgi?ID=C7664417&Mask=800#Electronic-Spec [3] https://en.wikipedia.org/wiki/Ammonia_(data_page) [4] http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html [5] http://www.chem.purdue.edu/gchelp/vibs/n2.html [6] Roger L. DeKock; Harry B. Gray; Harry B. Gray (1989). Chemical structure and bonding. [7] http://chemwiki.ucdavis.edu/Wikitexts/UC_Davis/UCD_Chem_2A/UCD_Chem_2A%3A_Hayashi [8] https://www.researchgate.net/publication/289539333_The_Reactivity_of_Fluorine