ModAGSTest1
Ammonia Molecule
Optimisation
Molecular Formula=NH3
N-H bond length= 1.01798 Angstroms
H-N-H bond angle=105.7446°
Calculation Method= RB3LYP
Basis Set= 6-31G(d,p)
Final Energy=-56.55776873 a.u.
RMS gradient= 0.00000323 a.u
Point Group= C3V
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
Ammonia |
This optimisation file is linked to here
Vibrations
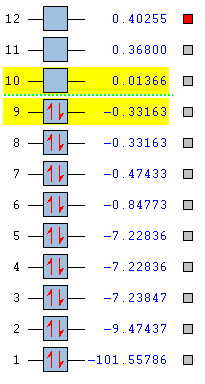
This is a non-linear molecule so due to the 3N-6 rule, 3 modes would be expected on the IR spectrum. As shown in the table the modes 2&3 are degenerate as well as 4&5. Modes 1,2 &3 are all "bending" vibrations whereas modes 4,5&6 are "bond stretching" vibrations. Mode 6 is highly symmetric and mode 1 is given the term of "umbrella" mode due to its appearance. On experimental spectrum of gaseous ammonia, 4 bands would be expected but 3 may be seen due to merging of 2 modes at around 3500.
Charges

The charges are distributed in this way mainly because nitrogen is a lot more electronegative than hydrogen so the electrons are placed nearer to it resulting in the nitrogen being negatively charged and the hydrogens being positively charged. The charges on the hydrogens are all the same because they're all in exactly the same environment and they all add up to cancel out the negative charge on the nitrogen because its a molecule with no overall charge.
Nitrogen Molecule
Optimisation
Molecular Formula=N2
N-N bond length= 1.09200 Angstroms
Calculation Method= RB3LYP
Basis Set= 6-31G(d,p)
Final Energy=-109.52359111 a.u.
RMS gradient= 0.02473091 a.u
Point Group= D∞h
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Nitrogen |
This optimisation file is linked to here
Vibrations

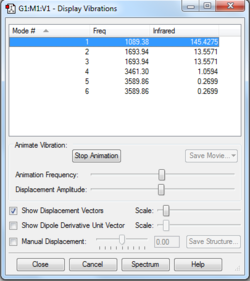
This is a linear molecule so due to the 3N-5 rule, 1 mode would be expected on the IR spectrum. As shown in the table, there is only 1 mode with a frequency of 2457.
Hydrogen Molecule
Optimisation
Molecular Formula=H2
H-H bond length= 0.6000000 Angstroms
Calculation Method= RB3LYP
Basis Set= 6-31G(d,p)
Final Energy=-1.19151183 a.u.
RMS gradient= 0.09719500 a.u
Point Group= D∞h
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Hydrogen |
This optimisation file is linked to here
Vibrations
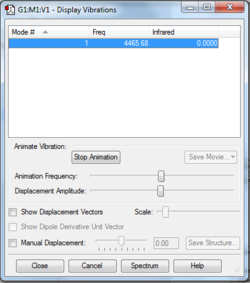
This is a linear molecule so due to the 3N-5 rule, 1 mode would be expected on the IR spectrum. As shown in the table, there is only 1 mode with a frequency of 4465.68.
Haber-Bosch Reaction
Reaction Equation: N2 + 3H2 --> 2NH3
Energy Calculation
In atomic units:
E(NH3)= -56.55776873 E(N2)= -109.52359111 E(H2)= -1.19151183 ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.01741086
In kJ/mol:
ΔE= -45.71221641
As this reaction is exothermic, this means that the ammonia product is more stable than the gaseous reactants.
Hydrogen Chloride
Optimisation
Molecular Formula=HCl
H-Cl bond length= 1.2900000 angstroms
Calculation Method= RB3LYP
Basis Set= 6-31G(d,p)
Final Energy= -460.80077017 a.u.
RMS gradient= 0.00135233 a.u
Point Group= C∞v
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000090 0.000300 YES Maximum Displacement 0.000139 0.001800 YES RMS Displacement 0.000197 0.001200 YES
Hydrogen Chloride molecule |
This optimisation file is linked to here
Vibrations

This is a linear molecule so due to the 3N-5 rule, 1 mode would be expected on the IR spectrum.
Charges

The charges are distributed in this way because chloride is a lot more electronegative than hydrogen so it places a greater force on the electrons which pulls them closer to it resulting in the chlorine being negatively charged and the hydrogen being positively charged.
Molecular Orbitals
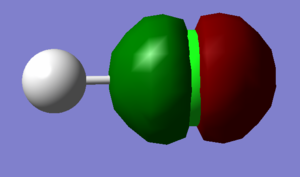

Hydrogen has a electronic configuration of 1s2 whereas chlorine has an electronic configuration of 1s22s22p63s23p5. The third and fourth molecular orbitals (shown on left) are occupied and non-bonding and they are both formed just from the 2p atomic orbitals on the Chlorine (third one is from 2px and the fourth one is from the 2pz orbital). They are both equivalent in energy as shown in the table on the right hand side and this energy level is very deep compared to other molecular orbitals so they're not involved in bonding as the energy gap is too large. The eighth and ninth molecular orbitals are also degenerate, occupied and are non-bonding. They are formed out of just the 3p atomic orbitals on the Chlorine and are the highest occupied molecular orbital. Finally, the tenth molecular orbital has been contributed to by the 1s orbital on hydrogen and a 3p orbital on Chlorine (any direction) and it is the lowest unoccupied molecular orbital. It is called σ*3pz and is non-bonding.