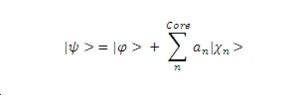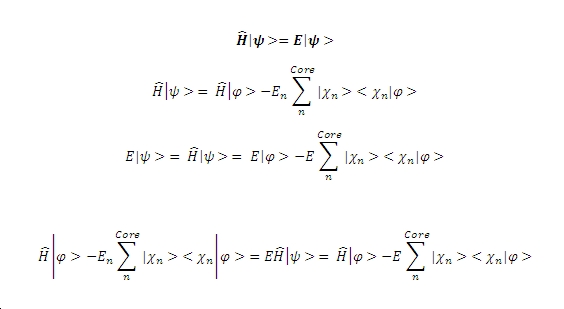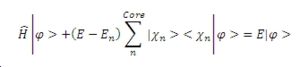Mod:MathematicalPseudoPotentialJustification

Mathematical Justification of Pseudo Potentials

Following the mathematics presented by clearly demonstrates that the pseduo-wave function is of the same energy as valence electron wave function. Unfortunately the mathematics editing facility on the wiki is currently not functioning so instead equations have been saved and inserted as image files. First one must consider what it is we want a pseudopotential to do. We want it to model in a smooth manner the with the wave function for a valence electron, so consider the wave function defined below with a constant term added for the core electrons states.

As has already been mentioned the valence electron wave function must be orthogonal to the core electron wave function, this allows us to determine a substitution for the value of a_n. Substituting this into the equation defined in part 1 gives a new version of the same wave function.

If the Schrodinger equation is then considered along with the fact that we assign an energy Eigenvalue of E_n the following result comes from the substitution and rearrangement:

From the equation it is clear that two operators now exist, one is the Hamiltonian whilst the other is an operator for the potential energy of the nucleus, condensing the equation into operator form therefore gives the following results.

The final equation then shows how the energy of the smooth function (pseudo-wavefunction) that includes a term for pseudo-potential is of the form as the valence electron wave function. This means that the method of pseudopotentials is valid.