Mod:MH5015

This page provides the results of simulations done by Martin Holicky in March Molecular modelling lab. All simulations were done using Gaussian 09.

Ammonia molecule optimisation

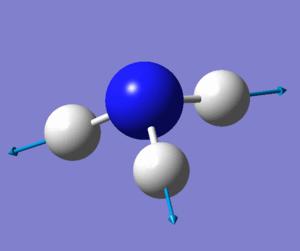
Ammonia is a very important molecule used in many industrial processes, such as fertilizer production. The structure is a trigonal pyramid, with the point symmetry C_3V.

The structure optimisation and frequency calculations were performed using the RB3LYP method and the 6-31G(d,p) basis set. The results are summarised in the table below and the LOG file is available here. Due to a large difference in electronegativity (N 3.02, H 2.20) and the non-symmetric geometry ammonia molecule was found to be polarised with a dipole moment of 1.8465 Debye. The charges on the atoms were found to be 0.378 (hydrogen) and -1.125 (nitrogen) and such charge distribution is within expectations.

Property	Value
E(RB3LYP)	-56.55776873 au
RMS gradient	0.00000485 au
N-H bond length	1.018 A
H-N-H angle	105.75 Deg
H-N-H-H dihedral angle	-111.86 Deg
Dipole moment	1.8465 D

Ammonia

Item table
|Item               Value     Threshold  Converged? | Maximum Force            0.000006     0.000450     YES | RMS     Force            0.000004     0.000300     YES | Maximum Displacement     0.000014     0.001800     YES | RMS     Displacement     0.000009     0.001200     YES | Predicted change in Energy=-1.141654D-10 |

Ammonia molecule "umbrella" vibration.

Vibrational properties

Since ammonia contains 4 atoms, from the 3N-6 rule six vibrational modes are expected. Indeed, Gaussian09 found 6 vibrational modes.

Wavenumber / cm-1	IR intensity	Assigment	Note
1089.5	145.38	"Umbrella" mode, symmetric bends
1693.5	2 x 13.55	asymmetric HNH bends	Two degenerate modes
3461.3	1.06	symmetric N-H stretch
3589.8	2 x 0.27	asymmetric N-H stretch	Two degenerate modes

In order for the molecule to be IR active, one of the requirements is that there must be dipole moment change with vibrations. In other words, the more symmetric the mode is, the smaller the absorbance is. All four non-degenerate modes have IR intensity greater than 0, so in the IR spectrum four peaks could be expected (strong, medium, weak and very weak). Experimental ammonia spectrum (NIST WebBook database [1]) contains three major peaks - 950 cm^-1, 1630 cm^-1, and 3330 cm^-1_. These observed peaks are in some agreement with the results of the simulations. The highest symmetry is for the asymmetric N-H stretch since its IR intensity is the lowest.

Hydrogen molecule

The structure optimisation and frequency calculations of a hydrogen molecule (H₂) were performed using the RB3LYP method and the 6-31G(d,p) basis set. The results are summarised in the table below and the LOG file is available here.

Property	Value
E(RB3LYP)	-1.17853936 au
RMS gradient	0.00000017 au
H-H bond length	0.743 A
Dipole moment	0 D
Point group	Dinfh

Item table
| Item Value Threshold Converged? | Maximum Force 0.000000 0.000450 YES | RMS Force 0.000000 0.000300 YES | Maximum Displacement 0.000000 0.001800 YES | RMS Displacement 0.000001 0.001200 YES |

Hydrogen molecule structure

Nitrogen molecule

The structure optimisation and frequency calculations of a nitrogen molecule (N₂) were performed using the RB3LYP method and the 6-31G(d,p) basis set. The results are summarised in the table below and the LOG file is available here.

Property	Value
E(RB3LYP)	-109.52412868 au
RMS gradient	0.00000060 au
N-N triple bond length	1.106 A
Dipole moment	0 D
Point group	Dinfh

Item table
| Item Value Threshold Converged? | Maximum Force 0.000001 0.000450 YES | RMS Force 0.000001 0.000300 YES | Maximum Displacement 0.000000 0.001800 YES | RMS Displacement 0.000000 0.001200 YES |

Nitrogen molecule structure

Molecular orbitals of nitrogen

MO diagram for a nitrogen molecule.

The nitrogen molecule contains 14 electrons, which occupy 7 molecular orbitals as shown in the diagram. There are two degenerate pi-orbitals (marked as #5 and #6). The first two orbitals are formed from the core 1s electrons, σ and σ*. The orbital #3 is a σ bonding orbital from 2s, #4 σ bonding orbital from 2p and #5 #6 are two degenerate π orbitals from 2p. Finally, #7 is a π* orbital from 2p orbitals. The overall bond order is 3.

Molecular orbitals of nitrogen. From left to right: 1σ (from 1s orbitals, #1), 1σ* (from 1s orbitals, #2), 1σ (from 1s orbitals), 2σ (from 2s orbitals, #3), 1π (from 2p orbitals, #5 and #6) and 1π* (from 2p orbitals, #7).

Haber-Bosch process calculations

The Haber-Bosch process is a very important synthetic route for production of a key chemical feedstock, ammonia. As the molecular nitrogen is a very inert gas, the reaction is done at high temperatures and pressures, along with catalysts.

N₂ + 3 H₂ → 2 NH₃

By comparing the energies of the reactants and products, the reaction was found to be exothermic, with energy change of -0.05579024 a. u. (-146.48 kJ/mol). The calculations are listed below.

	Energy / a.u.
E(NH3)	-56.55776873
2 E(NH3)	-113.115537
E(N2)	-109.52412868
E(H2)	-1.17853936
3 E(H2)	-3.53561808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=	-0.05579024

Uranium hexafluoride structure optimisation

Uranium hexafluoride structure with incorrect pseudopotential setup (LANL2DZ ECP).

Uranium hexafluoride structure (both LANL2DZ ECP and SDD yielded very similar structures).

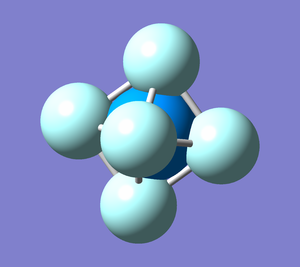
Uranium hexafluoride (UF₆) is an important intermediate in uranium enrichment and processing. Its structure is octahedral (Oh point group), with the U-F bond length approximately equal 2.03 A (found in SDS; identifier BELBOJ).

Elements with higher atomic numbers, such as uranium, are not part of the basis set used for previous calculations (6-31G(d,p)). Another basis set had to be used and two were tried - LANL2DZ ECP (downloaded from the EMSL Basis Set Exchange [2]) and SDD (Stuttgart/Dresden ECP, part of Gaussian09 by default).

LANL2DZ ECP basis set

The structure optimisation and frequency calculations of a UF₆ molecule were performed using the RB3LYP method and the GENECP / LANL2DZ ECP basis set. At first the simulation was accidentaly done with incorrect pseudopotential setup, which unsurprisingly produced an incorrect structure (square bipyramid, bond length 0.789 A). Nevertheless, it is interesting to report even this incorrect structure for educational purposes (i.e. how to recognise this type of error in the future). The later calculations with correct pseudopotentials produced a structure with U-F bond lengths of 2.03 A, which are in excellent agreement with the experiemental value of 2.03 A. Similarly to ammonia, there is a large difference of electronegativities (F 4.0, U 1.4). The fluorine atoms bear negative charge of -0.290 and the uranium atom positive charge of 1.738 (Mulliken method). Because the molecule is symmetrical, it has no net permanent dipole moment.

Charge distribution on UF (LANL2DZ basis set, Mulliken method).

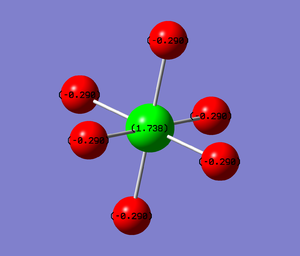
Incorrect pseudopotential setup

Log file: here

Property	Value
E(RB3LYP)	-3778.37466216 au
RMS gradient	0.00010730 au
U-F bond length	0.789 A
Point group	Oh

Item table
| Item Value Threshold Converged? | Maximum Force 0.000201 0.000450 YES | RMS Force 0.000087 0.000300 YES | Maximum Displacement 0.000001 0.001800 YES | RMS Displacement 0.000000 0.001200 YES |

Correct pseudopotential setup

Log file: here

Property	Value
E(RB3LYP)	-650.922348228 au
RMS gradient	0.00001008 au
U-F bond length	2.036 A
Point group	Oh

Item table
| Item Value Threshold Converged? | Maximum Force 0.000006 0.000450 YES | RMS Force 0.000003 0.000300 YES | Maximum Displacement 0.000023 0.001800 YES | RMS Displacement 0.000010 0.001200 YES | Predicted change in Energy=-4.378431D-10 |

SDD basis set

For comparison, another basis set and calculation method was tried. The structure optimisation and frequency calculations of a UF₆ molecule were performed using the MP2 method and the SDD basis set. The results are summarised in the table below and the LOG file is available here. The resulting bond length is slightly different from the LANL2DZ basis set, but there is a significant difference in the energy (-1076 vs -651 a. u.).

Property	Value
E(RB3LYP)	-1076.54819405 au
RMS gradient	0.01204746 au
U-F bond length	1.980 A
Point group	Oh

Item table
| Item Value Threshold Converged? | Maximum Force 0.000004 0.000450 YES | RMS Force 0.000002 0.000300 YES | Maximum Displacement 0.000012 0.001800 YES | RMS Displacement 0.000005 0.001200 YES | Predicted change in Energy=-1.284650D-10 |

Vibrational properties

For a 7-atomic molecule, 15 vibrational modes are expected. The data in the table below are based on the calculations with the LANL2DZ ECP basis set. Out of these these 15 modes, many are degenerate and there are 6 different frequencies. Only two modes (6 degenerate) are IR active as other modes were found to be highly symmetrical. The experimental values observed by Hawkins et al. were 186 and 623 cm^-1, in reasonable agreement with the wavenumbers found here. The wavenumbers found by the SDD basis set for the IR-active bands were 181.03 and 618.68 cm^-1, respectively, slightly closer to the experimental values.

Wavenumber / cm-1	IR intensity	Type	Note
142.13	3 x 0	bending	Three degenerate modes
168.56	3 x 0	bending	Three degenerate modes
182.74	3 x 15.37	bending	Three degenerate modes
524.48	2 x 0	stretching	Two degenerate modes
607.43	3 x 163.20	stretching	Three degenerate modes
612.17	0	stretching

Molecular orbitals

Uranium hexafluoride has much more complicated molecular orbitals compared to a nitrogen molecule. The molecule has 134 electrons. However, to simplify calculations, the core electrons on uranium were simulated as pseudopotentials and therefore the MO diagram contains less electrons. The molecular orbitals are composed of various combinations of p and s bonding and antibonding interactions. The lowest unoccupied MO is from the f-orbital on uranium. The diagrams are based on the calculations using the LANL2DZ ECP basis set.

MO diagram for UF₆. (LANL2DZ)

MO shapes for UF₆. From left to right: pseudopotential core on U (#7), σ interaction between fluorine s and uranium p (#8), p bonding interaction (#23), p antibonding interaction (#33), LUMO: uranium d orbitals (#35)