Jump to content

Mod:Hunt Research Group/BmimBF4 equilibration

From ChemWiki

Equilibration of 216 pairs of [bmim][BF4] or [bmim][NO3] (Notes by Ling)

[bmim][BF4] has no melting point, glass transition something around -85ºC and decomposes at around 400ºC [bmim][NO3] has multiple solid-solid transitions, melting point around 309K=36ºC

1. Details of simulations

In all the simulations the bond lengths and angles in the ring and to the attached carbon atoms were held rigid. The potential is from Ruth (Amber forcefield from Mario).

Simulations were performed using the program DL-POLY. The long range electrostatics were treated by Ewald summation. The simulations contained 216 ion pairs and the box sizes were adjusted to give close to zero pressure. After extensive equilibration (a. T=5K for 50 steps of NVE, timestep 0.2fs; b. T=400K for 1000 steps of NVE, timestep 2fs; c. T = 400K for 4 runs of 30ps of NVT, timestep 2fs) and (d. T= 400 K for 40ps of NVT with 10ps equilibration, timestep 2fs, with a Nose-Hoover thermostat (0.1); e. T=400 K for 15 ps of NVE, timestep 1fs), I check the volume with (f. T = 400K for 30 ps of NPT, timestep 2fs with a Nose-Hoover thermostat (0.1)), and last production run (g. T = 300K for 200ps of NPT, timestep 2fs with a Nose-Hoover thermostat barostat (0.1 0.1)).

The parameters in the CONTROL file are as below: 

temperature          400
ensemble   nvt  hoover  0.1
steps                20000
equilibration        5000
cap
scale                5
zdensity
print                10
traj                 20 30 0
stats                1
quaternion       1.0E-8
rdf 5
print rdf
timestep         0.002 ps
cutoff           14.000
delr width       0.75000
rvdw cutoff      11.0000
ewald precision  1.0E-6


2. Results

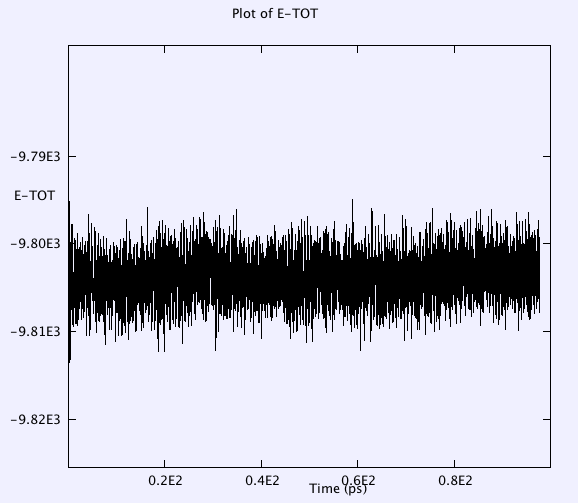
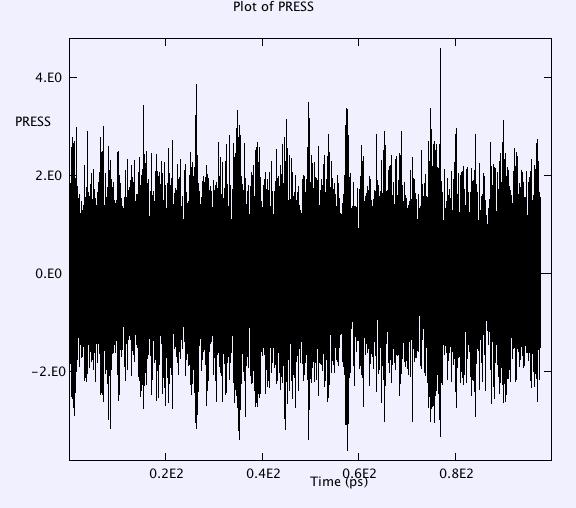
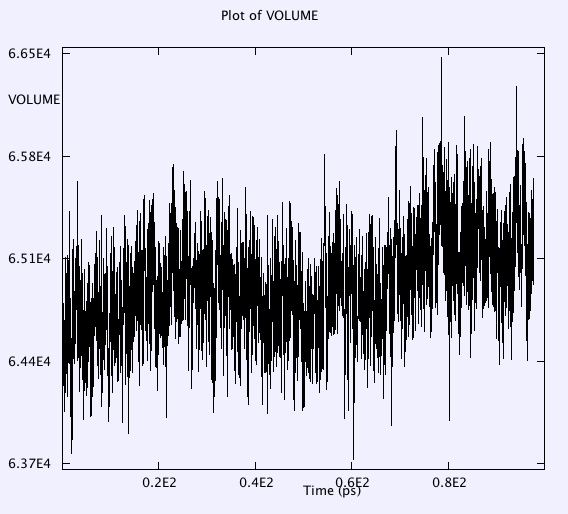
Temperature, Etot, volume, pressure, pressure tensor, radial distributions of anions are monitored throughout the whole simulation. Selected results after major check points (e.g. a, b, c, d, e, f, g listed above) are as below:

a. T=5K for 50 steps of NVE, timestep 0.2fs

this step is to relax the structure (as if we are starting from a CONFIG that only contains atom positions, the forces might be too large), and we have to use smaller timestep (e.g. 0.2fs) to make pressure tensor ~E+00, and final T = 6.5K. If use large timestep e.g. 2fs, pressure tensor ~E+06.

b. T=400K for 1000 steps of NVE, timestep 2fs

working fine. ended at 365K. pressure tensor small.

c. T = 400K for 4 runs of 30ps of NVT, timestep 2fs

working fine. 

      Average pressure tensor                                       r.m.s. fluctuations

          3.6847E+00  2.8171E-01  3.7964E-02                          1.3755E+00  9.2061E-01  9.2664E-01
          2.8171E-01  3.7492E+00 -2.5815E-02                          9.2061E-01  1.3102E+00  9.2260E-01
          3.7964E-02 -2.5815E-02  3.6313E+00                          9.2664E-01  9.2260E-01  1.3774E+00

              trace/3.   3.6884E+00

d. T= 400 K for 40ps of NVT with 10ps equilibration, timestep 2fs, with a Nose-Hoover thermostat (0.1)

Average pressure tensor r.m.s. fluctuations 

          4.2137E+00  1.9944E-01 -2.7816E-03                          1.4756E+00  9.5787E-01  1.0092E+00
          1.9944E-01  4.3286E+00  1.9120E-02                          9.5787E-01  1.4036E+00  9.6415E-01
         -2.7816E-03  1.9120E-02  4.3524E+00                          1.0092E+00  9.6415E-01  1.4451E+00

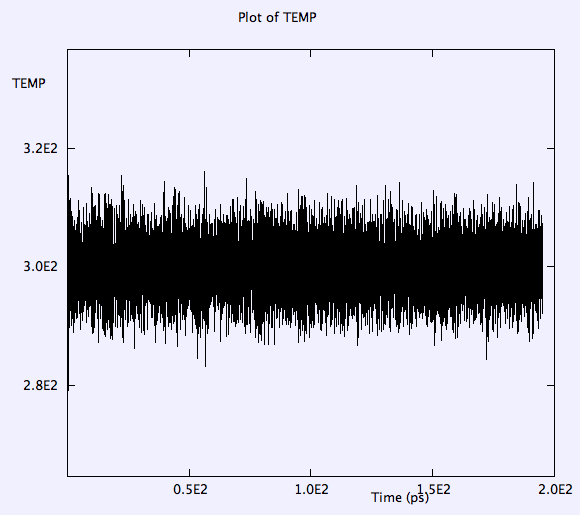
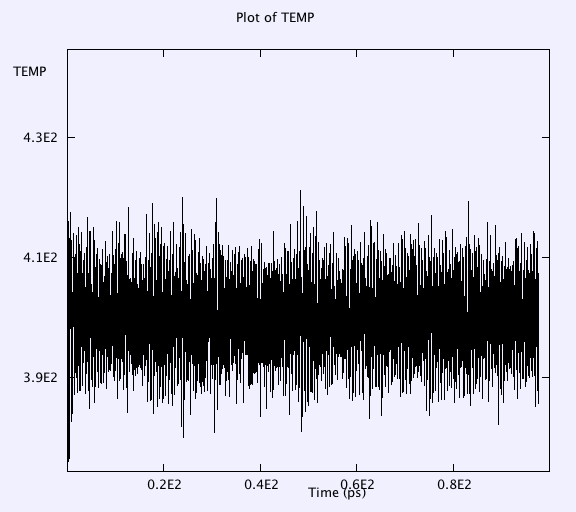
Thermostat is working fine and temperature oscillations is within 20 K around 400 K in the last 30ps when 'equilibration' is turned off.

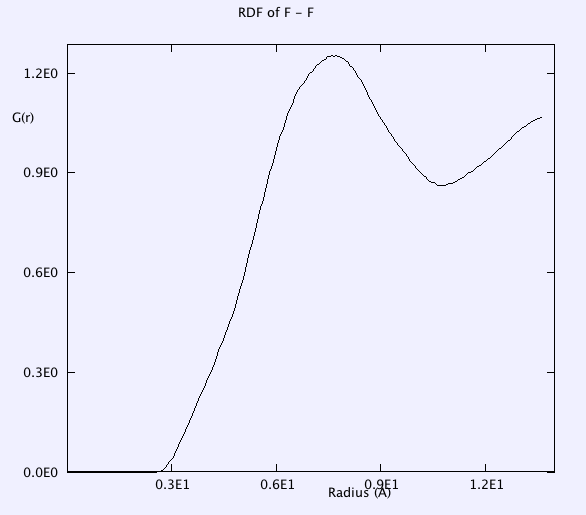
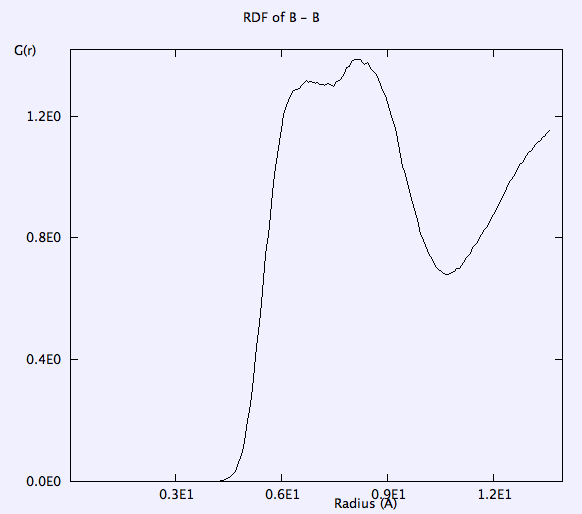
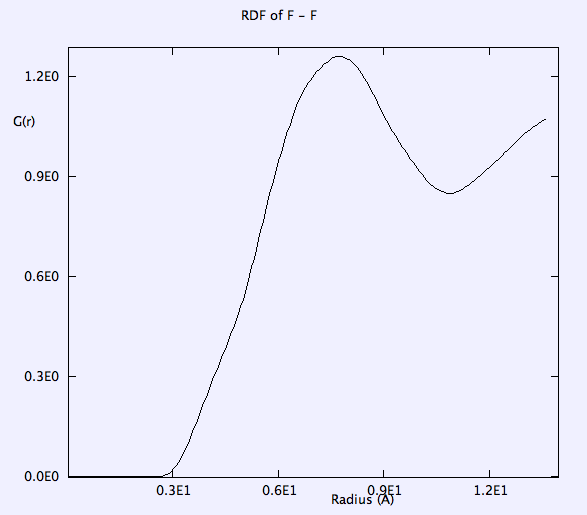
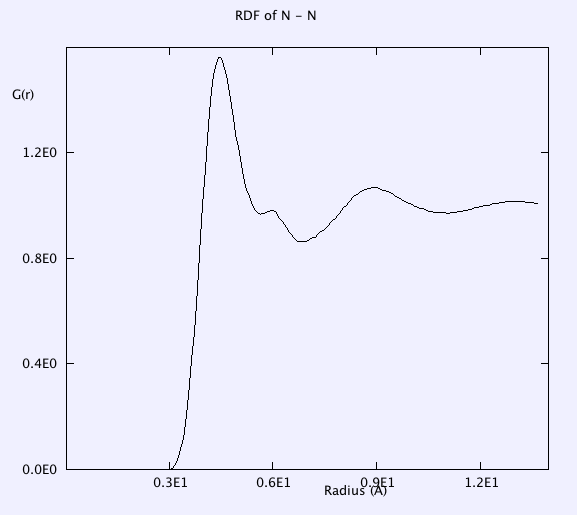
RDF of B-B, and F-F is smooth. g(r) takes the value of unity at large r => completely random distribution (i.e. liquid).

e. T=400 K for 15 ps of NVE with no equilibration, timestep 1fs (or 2fs)

The temp oscillates around 420K, not drift, conserved perfectly.

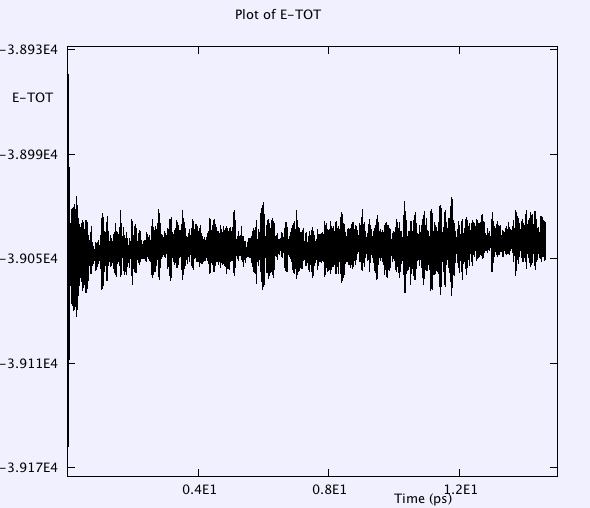
Etot has smaller oscillations in the 1fs timestep case than in the 2fs case.

g. T = 300K for 200ps of NPT with no equilibration, timestep 2fs with a Nose-Hoover thermostat barostat (0.1 0.1) 

              Average pressure tensor                                       r.m.s. fluctuations

         -4.6864E-02  1.4464E-01  9.2091E-02                          1.2225E+00  8.2690E-01  8.3070E-01
          1.4464E-01  4.9626E-02  2.1433E-02                          8.2690E-01  1.1646E+00  7.9846E-01
          9.2091E-02  2.1433E-02  1.8390E-03                          8.3070E-01  7.9846E-01  1.1957E+00

           trace/3.   1.5336E-03

Approximate 3D Diffusion coefficients (10^-11 m^2 / s) 

           atom        D
           N1         1.5018
           C2         1.8950
           N3         1.4990
           C4         3.2406
           C5         3.3154
           C6         3.8673
           C7         3.7785
           C8         1.6892
           C9         2.0309
           C10        3.3126
           H5         5.6477
           H3         7.2251
           H4         7.4695
           HM1        2.4484
           HB1        2.6266
           HB2        2.6111
           HB3        2.8469
           HB4        3.9777
           B          0.70278
           F          1.0379

Note: These are estimates of the diffusion coefficient in the OUTPUT file for the different atomic species in the simulation. These are determined from a single time origin and are therefore approximate. Accurate determinations of the diffusion coefficients can be obtained using the msd utility program, which processes the HISTORY file. (Ask Ruth how to use the MSD in the gui program). If an NPT simulation is performed the OUTPUT file also provides the mean pressure (stress tensor) and mean simulation cell vectors.

Ref: Liu06, at 298K, Nose-Hoover NPT 0.7 0.03, 2fs and 0.2 fs, 128 molecules, 200ps production run. The self-diffusion coefficient of component i can be calculated by the Einstein relation (Ref: Mor02) D_i = 1/6lim_{t→infinity}d/dt<[r_i(t) - r_i(0)]²>

where the quantity in <> is the ensemble-averaged mean square displacement (MSD) of the species i, and r_i is the vector coordinate of the centre of mass. The self-diffusion coefficients were obtained from the slope from 20-100ps and applying the above equation.

Cation 0.9 Anion 0.6 united-atom force field (UA),

Cation 1.2 Anion 0.8 all-atom force field (AA),

Cation 1.4 Anion 1.3 exp (pulsed field gradient spin-echo NMR, Ref: Nod01, Tok04).

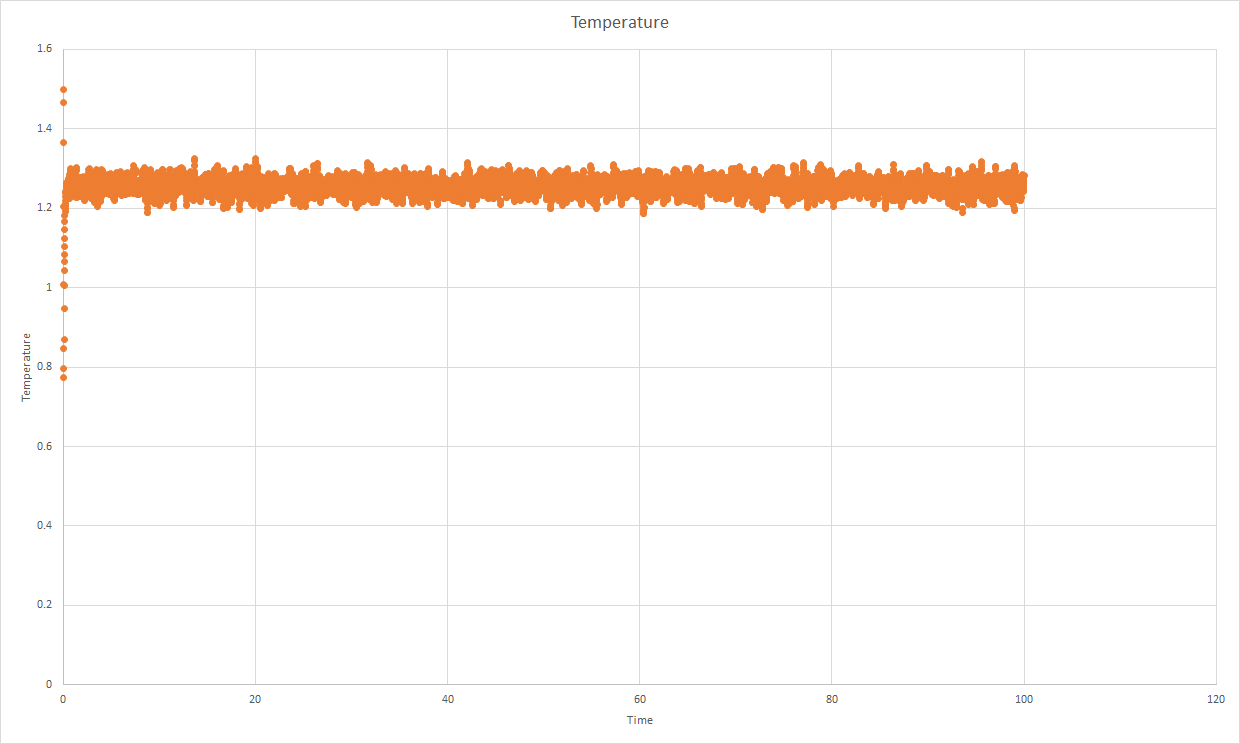
Density of [bmim][BF4]: 1.188 g cm^(-3) at 300K.

Ref: Liu06, at 298K, Nose-Hoover NPT 0.7 0.03, 2fs and 0.2 fs, 128 molecules, 200ps production run.

1.208 united-atom force field (UA),

1.194 all-atom force field (AA),

1.211 exp.

Note: have used the same procedure to equilibrate [bmim][NO3]. So I just list the final results (i.e. after step g: T = 400K for 100ps of NPT with no equilibration, timestep 2fs with a Nose-Hoover thermostat barostat (0.1 0.1) ) for [bmim][NO3] here.

Average pressure tensor r.m.s. fluctuations 

         -1.1824E-01  5.0155E-02  8.7242E-02                          1.4538E+00  9.7425E-01  9.9123E-01
          5.0155E-02 -2.5461E-02 -1.5140E-01                          9.7425E-01  1.4039E+00  9.4966E-01
          8.7242E-02 -1.5140E-01  1.4937E-01                          9.9123E-01  9.4966E-01  1.3776E+00

Approximate 3D Diffusion coefficients (10^-11 m^2 / s) 

           atom        D
           N          3.4248
           C          4.6215
           CT         5.5992
           H5         6.1452
           H4         7.8411
           H1         6.3107
           HC         7.4128
           OS         3.0343

Ref: Mic06: Table 4: cation 8.3, anion 8.0.

Density of [bmim][NO3]: 1.111 g cm^(-3) at 400K.

Ref: Mic06, 1.1124 g cm^(-3) at 363.15K, Berendsen thermostat (0.1ps) and barostat (1.0ps), GROMACS.

Exp: Bak01, 1.1120 g cm^(-3) at 363.15K.

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Mod:Hunt_Research_Group/BmimBF4_equilibration&oldid=558086"