Mod:Gaussian

The Meaning of Optimisation in Gaussian

In order to optimise the molecular structure of the input, a potential energy surface (PES) is used. This usually involves two degrees of molecular freedom and forms a surface by plotting the energy above the plane. The height of a structure on the surface is equal to that particular conformations energy. In general there are three types of stationary points one must consider when evaluating a PES these are:

1. Maxima - these represent areas of maximum energy and are found by calculus since f'(x,y)=0 and f"(x,y)<0 at maxima.

2. Minima - these represent areas of minimum energy and are also found by calculus since f'(x,y)=0 and f"(x,y)>0 at minima.

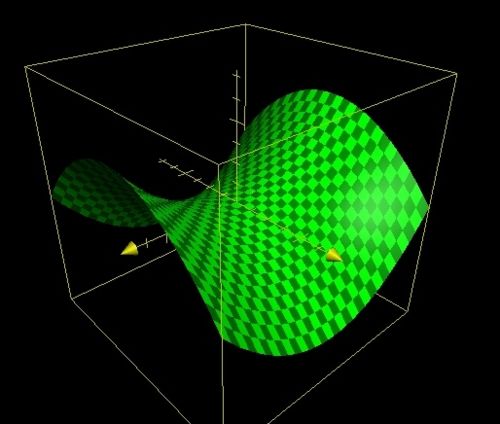
3. Saddle Points - are the three dimensional equivalent of a 2D point of a inflection defined by f'(x,y)=0 and f"(x,y)=0.

Maxima/Minima	Saddle Point
f(x,y)=10sin(x/2)sin(y/2)	f(x,y)=x2-y2

Examples of all 3 stationary points can be found above, these were plotted using the functions given in the table on the 2005 Apple Computer Inc Grapher (version 1.1) software. There are then two types of extrema local and global. A local point represents a stationary point that is the extrema for a particular region of the PES. A global extrema represents an extrema for the entire surface. In an optimisation program the algorithm used seeks to find a stationary point. This stationary point is hopefully the global minima. It is however possible for the algorithm to get stuck in a local minima and therefore return an optimised structure that is not of the lowest possible energy. In an attempt to prevent the optimisation from becoming stuck in a local minima Gaussian has 4 criteria that must be satisfied for an optimisation to converge, these are listed below.

• The forces must be less than 0.00045. This is effectively saying that the forces must be 0. Forces are critical since force is the negative differential of potential (F=-dV/dt). Hence at an extrema the force will equal zero since the differential of potential equals 0.

• The root mean square of force must be below 0.0003. A root mean square force esentially gives a statistical measure of the size of the force.

• The calculated displacement of the subsequent step must be less than 0.0018. That is the distortion to the molecular geometry must be very small for the next step

• The root mean square of displacement must be less than 0.0012

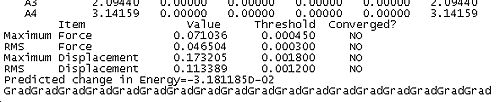
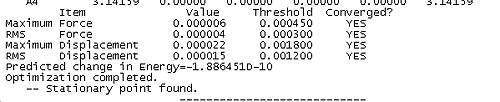
Together these criteria serve to reduce the likelihood of Gaussian predicting a minimum to early in a calculation. Reading the output from an optimisation can yield some useful and interesting data as well as demonstrating the application of the above criteria for convergence in the algorithum. In the case of BH₃ the convergence can be achieved in 5 steps. The table below shows snapshots of the first and last step in the convergence, note that the energy of the final molecule is calculated and printed in the penultimate step of the optimisation.

Optimisation Output
Step 1	Final Step

Immediately after the convergence criteria are satisfied the final molecular structure is printed. This also prints the optimised molecular parameters of bond length, bond angle and dihedral angle. The outputs for BH₃ can be seen below:

Optimisation Output
Initial	Converged

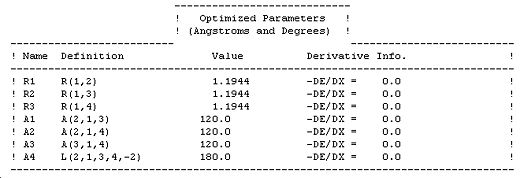
Levels of Theory

Hartree-Fock Approximation (HF)

First introduced around 1927 the HF approximation is used to give approximate solutions to quantum mechanical problems that are not solvable exactly. The HF approximation relies on the use of molecular orbitals (MOs) and more specifically the linear combination of atomic orbitals (LCAO). In the HF approximation the motion of each electron in a system is described by a MO, with each MO being made up of a LCAO. In HF the linear expansion co-efficients for the LCAO are solved. This must be done iteratively since the co-efficients depend on themselves. For this reason the HF is referred to as a self-consistent field theory (SCF). The MOs themseleves are the product of HF theory and are therefore (except in the case of hydrogen) not real molecular orbitals but rather an approximation to the Schrödinger equation. Under the HF approximation an electron can only feel the average Coulombic forces of the other electrons in the system and this is often a poor approximation. The electron correlation term is determined in more advanced theories such as DFT and MP2. For a more detailed discussion follow this link.

Density Functionals Theory (DFT)

DFT is an established quantum mechanical model first proposed in the 1970's. This model relies on the Born-Oppenheimer approximation. That is the position of the nuclei are fixed from the point of view of the electron (since the nucleus is so large any movement of the nucleus will lead to an instantaneous movement of electrons). This is an extension of the HF approximation. In DFT, electrons are modelled via "general functionals" , where a functional is a function of another function. Current DFT models are composed of 4 terms in which the energy of molecule can be decomposed. These are a kinetic energy term, a nuclear-electron interaction term, an electron-electron repulsion term and an exchange correlation term. The last term can be further divided into a correlation and exchange term, and as with all terms (except nuclear-nuclear interactions) be determined from electron density calculations. All terms except the exchange-correlation term can be thought of in terms of classical physics. The difficulty in calculating a DFT is determining the exchange-correlation term. This is only known for the free electron gas but can be approximated by integration. Gaussian approximates the exchange correlation term via numerical integration usually through a hybrid functional (a hybrid functional involves the use of Hartree-Fock and other {model dependent} functionals). In this lab DFT calculations have been run using the B3LYP method. This means Gaussian is solving the hybrid functional shown below in order to determine the exchange-correlation energy:

This may seem to be a relatively simply formula but when just a few of the terms are expanded one is glad that the computer is capable of numerically solving such functions! For a more detailed treatment see this page

Møller-Plesset Pertubation Theory (MP2)

When a perturbation is used a problem that cannot be solved exactly is approximated. This is done by using a similar problem that can be solved exactly and a "power series" of small terms that move from the exactly solvable to the solution that is to be approximated. This is done by taking an exact solution and adding to it a series of small parameters. These small parameters home in on the solution to the approximation until a reasonably accurate approximation is achieved. The MP2 level of theory, was first published in 1934 and applies a perturbation to solve the electron correlation term and hence adds higher excitations to the HF approximation. For more information follow this link.

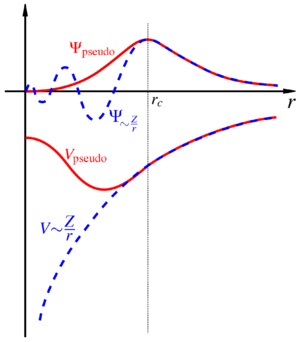
Pseudo-Potentials

For a mathematical justification follow this link

A pseduopotential removes the complicated effects of a systems core electrons. When a valence electron wavefunction passes through the core it oscillates rapidly to maintain orthogonality with the tightly bound core electrons. So in this approximation the core electrons are considered to have a pseudo-potential that then acts on the valence electrons pseudo-wavefunction. This pseudo-potential is designed to remove the rapid oscillations in the core region instead replacing it with a smooth more mathematically simplistic pseduo-wavefunction. Outside of the core region hte pseudo wave function behaves exactly as the valence electron wave function. Chemical physics demonstrates that the core electrons have little effect on the reactivity and properties of a species and thus the simplification is valided. This principle is demonstrated by figure below.

Image taken from http://en.wikipedia.org/wiki/Pseudopotential.

Basis Sets

Meaning of a Basis Set

Mathematically a basis set prvodes a description of all orbitals within a system, it is these orbitals that combine to approximate the total electronic wave function that is used in calculations. The larger a basis set the fewer restrictions that are placed on the position of the electron and hence the higher the closer the model to the true QM picture where an electron has some probability of existing anywhere. Many basis sets use linear combinations of gaussian functions to model a system. For a more in depth discussion of the meaning and formulation of a basis set see this website.

Minimal Basis Sets

These use fixed size atomic type orbitals and contain the minimum number of functions required to model an atom. This type of basis set is not used in this lab.

eg. STO-3G

Split Valence Basis Sets

In this case the basis set is made larger in comparison to a minimal basis set by increasing how many functions model each atom, so each valence orbital will have 2⁺ sizes of basis function.

eg. 3-21G

Polarized Basis Sets

In this case unlike in the split valence case the orbital shape is allowed to change as well as its size, this is achieved by the inclusion of orbitals with angular momentum beyond the ground state. This means that for example polarised basis sets will add d-orbitals to carbon.

eg. 6-31G*

Diffuse Functions

These are used when the orbitals are relatively far from the nucleus (eg molecules with lone pairs and systems with negative charge) since they allow large versions of s and p functions. By allowing larger versions of the s and p functions the orbitals can occupy a greater region of space.

eg. 6-31+G(d)

High Angular Momentum Basis Sets

These basis sets add multiple polarisation functions per atom (eg. 6-31(2d) adds two d-functions per heavy atom), these basis sets are not used in this lab and are not usually required for HF calculations but rather for calculations involving electron correlation methods.

eg. 6-31G(2d)

Post-Third-Row Atoms Basis Sets

In the case of very large atoms, electrons near the nucleus are approximated by effective core potentials, which include relativistic effects.

eg. LANL2DZ

Basis Sets Used in this Lab

Name	Description	Applicable Atoms	Number of Basis Functions for H atoms
3-21G	Split valence, 2 sets of functions in the valence region.	H to Xe	2
6-31G*	Adds polarisation function to heavy atoms.	H to Cl	2
6-31+G (d)	Adds diffuse functions-lone pairs, anions and excited states.	H to Cl	5
6-311+G(d,p)	Adds extra valence functions to 6-31+G(d)	H to Br	6
LANL2DZ	Uses core effects for all atoms heavier than Ne.	3rd row and beyond	-