Mod:Epoxide Computational Chemistry
A computational chemistry investigation.
Starting optimisations
20140222 Saturday
Having drawn this taxol precursor in ChemDraw Pro 13.0 and optimised it to this structure with the MMFF94 force field in Avogadro, which I called the O-up isomer in my file names, I then pulled the atoms around while Avogadro's perpetual force field optimiser was running to produce this other isomer, which I called the O-down isomer in my file names. This too I optimised at with the MMFF94 force field. Moving straight on to try to generate some NMR spectra for the sulphur-containing derivatives 17 and 18, I added a heterocyclic ring to each optimised structure by building in Avogadro's molecule editor, optimising both again at the MMFF94 level. I saved all my files as MOL files ready to import into GaussView to set up the more expensive calculations. Having a look at the paper with the spectroscopic references by Paqette, Pegg, Toops, Maynard, and Rogers (1990),[1] it seems that the geometry of the possible isomers is possibly fixed very nicely so that few conformers need be considered in finding the geometry of minimum energy: the fused ring systems have this 'rigid' property. The calculations might take some time nonetheless, so I first optimised the molecules to a minimum again, this time using the HF 3-21G model chemistry, not calculating force constants.
Once the first molecule was ready, I set up another optimisation, this time an optimisation and frequency calculation, calculating the force constants once, at the B3LYP 6-31Gdp level, letting the calculation run for a few minutes to make sure that things looked okay before submitting it to high performance computing (HPC) to deal with. I submitted the second molecule in the same way, so that both 'O-up' and 'O-down' sets of files were going to soon be optimised first at the MMFF94 level, then at the HF 3-21G level and then at the B3LYP 6-31Gdp level ready for calculating the NMR spectra for the molecules.
An example of the lines at the top of the Gaussian input file is shown here for the 'O-down' isomer:
%chk=C:\G09W\Scratch\20140222 Taxol derivative O down B3LYP 6-31Gdp opt freq 1a.chk
# opt freq b3lyp/6-31g(d,p) geom=connectivity
These were left to run overnight.
Trying to calculate the NMR spectrum for H2salen, a precursor for salcomine I had synthesised in the lab a few weeks ago, I submitted an optimisation and frequency calculation to Gaussian overnight a few days ago but the calculation had failed. Fingers crossed...
Returning to check the optimisations
20140223 Sunday
Both calculations ran successfully overnight and perhaps, since it is the weekend, partly into the day. The 'O-up' isomer shown here had an energy of -1612.49376171 a.u. and its vibrational frequencies (shown below - click to enlarge the image) showed that the calculations had indeed found an energy minimum, since all the frequencies were real.

The 'O-down' isomer shown here had a slightly higher energy of -1612.48877961 a.u. suggesting that it would occupy a smaller portion of an equilibrium between the two isomers studied. Again, this isomer's vibrational frequencies (below) were all real, showing that the calculation indeed optimised to an energy minimum as it should do.

Submitting NMR calculations
The O-up isomer 17 has experimental proton NMR data run in deuterated chloroform.[1] Checking the boxes to set up the calculation in GaussView, and entering the keywords 'freq' and 'EmpericalDispersion=GD3' the command line in the file (below) shows that the calculation not seems to be at the 'rb3lyp/6-31g(d,p)' level rather than the 'b3lyp/6-31g(d,p)' level. The 'r' before the 'b3lyp/6-31g(d,p)' seems to stand for 'restricted'...
%chk=C:\G09W\Scratch\20140223 O-up NMR freq B3LYP 6-31Gdp 1a.chk
# nmr=giao rb3lyp/6-31g(d,p) scrf=(cpcm,solvent=chloroform) geom=connectivity freq empiricaldispersion=gd3
Running this on the PC for a while to confirm that the calculation runs for a few minutes without crashing, this was then submitted to the HPC suite. A calculation was set up, for interest (to see any differences), with a default spin but otherwise identical with the following command line, and submitted too.
%chk=C:\G09W\Scratch\20140223 O-up NMR freq B3LYP 6-31Gdp 1b default spin.chk
# nmr=giao b3lyp/6-31g(d,p) scrf=(cpcm,solvent=chloroform) geom=connectivity freq empiricaldispersion=gd3
The proton NMR spectrum of the O-down isomer 18 in the literature was run in deuterated benzene instead of deuterated chloroform.[1] Attempting to set up the calculation again in this solvent for this isomer proved initially difficult, with the calculation crashing within seconds when run initially on the PC. Closing the program and trying again, with the following command line, the calculation seemed to run just fine initially.
%chk=C:\G09W\Scratch\20140223 O-down NMR freq B3LYP 6-31Gdp 1a default spin.chk
# nmr=giao b3lyp/6-31g(d,p) scrf=(cpcm,solvent=benzene) geom=connectivity freq empiricaldispersion=gd3
Leaving the calculations to run overnight, with fingers crossed again, it would be interesting to know how optimising the molecules first speeds up the calculations. With that in mind, the molecules were not optimised at the restricted level, so I will delete this calculation from the list and run it again, for interest, if time allows: recalculating again at a different level of theory would not be quick and efficient! (Done - the deleted calculation was reported to have run for one hour and fifteen minutes, it appears.)
NMR spectra of the isomers
20140224 Monday
The NMR calculation seems to have worked well, and the predicted spectra are ready for inspection. The proton spectrum simulated in chloroform (with 'TMS B3LYP/6-31G(d,p) Chloroform' as the reference choice) is shown below for the 'O-up' isomer 17. (Click the scalable vector image to enlarge it.)

The predicted proton NMR spectrum for the 'O-down' isomer 18 is shown below (with 'TMS B3LYP/6-31G(d,p) Benzene' as the reference choice).

Considering the two spectra together, might it be possible to find evidence that Paqette, Pegg, Toops, Maynard, and Rogers (1990) have assigned the correct isomers, 17 and 18, to their corresponding spectra?
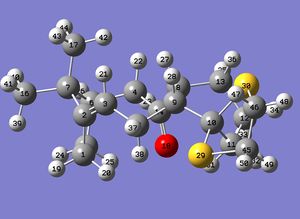
Looking at the numbering used in identifying the atoms in the molecule, it should be notes that the numbers are identical except that they go in exactly opposite directions around the sulphur-containing ring (click the numbering pictures below to enlarge). The numbering for isomer 17 is shown here:
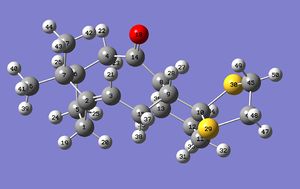
The numbering for 18 is shown here:
It appears that the program generating the NMR spectra is treating the molecule as rigid, with one proton (number 42) of one of the methyl groups much more deshielded (at 2.3 ppm) than the one nearest to the double bond (number 43 at 0.9 ppm). No conclusions possible yet...
Checking the frequencies of the molecules generated last night, while the 'O-down' isomer has only real vibrational frequencies, confirming that the calculation has located an energy minimum, (the bottom of the potential-energy valley,) the 'O-up' isomer has one imaginary frequency, -31.10 /cm, suggesting that the program has found a transition state (a conformation that is an energy maximum not an energy minimum - the top of a hill where the potential energy gradient does not change with atom coordinates but is an unstable one nonetheless). The molecules were both possessed of only real frequencies yesterday - one of them must have re-optimised its geometry overnight when the additional NMR calculation was performed.
Averaging the chemical shifts for the rotating methyl groups
20140225 Tuesday
The molecules' geometries were calculated at a theoretical temperature of zero Kelvin. The molecules in the literature would have been investigated at around three-hundred Kelvin (room temperature). At this temperature, the methyl groups would be rotating, indistinguishable on the NMR timescale. Having been doing some thinking overnight, without any calculations running on the computers, it appears to me now that the predicted signals for the individual protons in the methyl groups could be averaged together. The weighted average should replicate the literature values.
Starting with the O-down isomer 18 (optimised correctly to an energy minimum), protons numbered 39, 40 and 41 belong to one freely-rotating methyl group. Taking the mean value of their respective predicted chemical shifts in benzene with a TMS reference, 1.497021,0.975694 and 0.975694, gives their new predicted room temperature signal at 1.149469 ppm.
Protons numbered 42, 43 and 44 have chemical shifts at 1.32076, 1.221034 and 1.097374 ppm respectively, with a mean value of 1.213056 ppm, their new room temperature predicted signal.
| Chemical shift /ppm | Atom number |
|---|---|
| 5.31 | 21 |
| 3.28 | 47 |
| 3.12 | 27, 48 |
| 2.99 | 28, 31, 49, 50 |
| 2.62 | 22, 37 |
| 2.31 | 25, 38 |
| 2.18 | 20 |
| 2.04 | 19, 26 |
| 1.91 | 24 |
| 1.77 | 23, 32, 34, 36 |
| 1.50 | 33, 35 |
| 1.21 | 39, 40, 41 |
| 1.15 | 42, 43, 44 |
Attempting to group these as in the literature, the predicted chemical shifts for 18 can be quoted (making no assumptions about the splitting of peaks that are not multiplets except for the fair assumption that the rotating methyl groups will be singlets) and compared:
1H NMR (predicted, C6D6) chemical shift 5.31 (1H), 3.28 (1H), 3.12-2.99 (m, 6H), 2.62-2.31 (m, 4H), 2.18-1.77 (m, 8H), 1.50 (2H), 1.21 (s, 3H, Me), 1.15 (s, 3H, Me),
(lit.[1], 1H NMR (300 MHz, C6D6) chemical shift 5.21 (m, 1H), 3.00-2.70 (m, 6H), 2.70-2.35 (m, 4H), 2.20-1.70 (m, 6H), 1.58 (t, J = 5.4 Hz, 1H), 1.50-1.20 (m, 3H), 1.10 (s, 3H), 1.07 (s, 3H), 1.03 (s, 3H)).
My molecule seems to have two protons missing... funny that...
Ooops! I have been modelling the wrong molecule! Isomer 18 has three methyl groups, whereas the molecule I have been modelling has a proton on the ring junction where a methyl group should be. Back to the drawing board!
Adding a methyl group
Starting over, or, at least, making a slight modification and recalculating, a proton on the ring junction was substituted for a methyl group on my old version of the 'O-up' isomer 18 to make the 'real' isomer 18; the molecule was optimised at the HF/3-21G level on the PC and sent to the HPC suite for NMR calculations at the B3LYP/6-31Gdp level skipping the optimisation at this level. Hopefully the molecule will be optimised to an energy minimum this time, with positive frequencies only. The top lines form the submitted job:
%chk=C:\G09W\Scratch\20140225 O-up 18 nmr opt freq gd3 chloro B3LYP 6-31Gdp.chk
'#' opt=calcfc freq b3lyp/6-31g(d,p) scrf=(cpcm,solvent=chloroform) geom=connectivity nmr empiricaldispersion=gd3
For 'O-down' isomer 17, also initially missing its methyl group on the ring junction, the methyl group was simply popped onto the ring junction in place of the hydrogen; this molecule is already optimised to an energy minimum at the B3LYP/6-31Gdp level so this may be quicker (it would be interesting to know the difference in the calculation times). The command line from this submitted job:
%chk=C:\G09W\Scratch\20140225 O-down 18 nmr opt freq gd3 chloro (once) B3LYP 6-31Gdp.chk
'#' opt=calcfc freq b3lyp/6-31g(d,p) scrf=(cpcm,solvent=benzene) geom=connectivity nmr empiricaldispersion=gd3
Proton NMR prediction for the corrected structures
20140226 Wednesday
Last night's calculations produced optimised molecules 17 and 18 with real vibrational frequencies only, as hoped. The further optimisation of (and NMR calculation for) the already HF/3-21G optimised structure 17 was fastest, taking two hours and thirty minutes to run. The optimisation and NMR calculation performed on structure 18, in which the methyl group was substituted onto the erroneous structure without optimisation at the HF/3-21G level, took longer, taking three hours and eight minutes to run. Although the difference is not huge, it appears that building up the optimisation in steps of increasing computational expense is faster overall than going straight in at the most expensive level (although identical conformers should really be compared for a truly fair analysis).
The corrected 'O-up' isomer
The optimised structure of the corrected 'O-up' isomer 17, is shown here and is shown in the picture below with atom numbering (right clicking on the link in this paragraph, and choosing Style > Labels > With Atom Number will display numbers on the atoms).

Averaging the chemical shifts for the freely rotating methyl groups including the newly added methyl group (protons 51, 52 and 53), the table below shows the predicted chemical shifts for isomer 17.
| Chemical shift /ppm | Proton number |
|---|---|
| 5.15 | 21 |
| 3.31 | 48 |
| 3.22 | 49 |
| 3.26 | 27 |
| 3.01 | 46, 47 |
| 2.72 | 20, 37 |
| 2.40 | 22, 23, 30, 36 |
| 2.27 | 19, 24 |
| 2.12 | 26, 34 |
| 1.95 | 31 |
| 1.90 | 33 |
| 1.60 | 25, 32 |
| 1.49 | 35 |
| 1.46 | 41, 42, 43 |
| 1.17 | 51, 52, 53 |
| 1.14 | 38, 39, 40 |
Listing in groups and comparing as before, it seems possible to make the data fit; methyl groups, all attached to carbons with no protons, are all assumed to be a 3H singlet:
1H NMR (predicted, CDCl3) chemical shift 5.15 (1H), 3.31-3.01 (m, 5H), 2.72-1.60 (m, 14H), 1.49 (1H), 1.46 (s, 3H, Me), 1.17 (s, 3H, Me), 1.14 (s, 3H, Me),
(lit.[1], 1H NMR (300 MHz, CDCl3) chemical shift 4.84 (dd, J = 7.2, 4.7 Hz, 1H), 3.40-3.10 (m, 4H), 2.99 (dd, J = 6.8, 5.2 Hz, 1H), 2.80-1.35 (series of m, 14H), 1.38 (s, 3H), 1.25 (s, 3H), 1.10 (s, 3H), 1.00-0.80 (m, 1H)).
The computer model predicts three methyl group signals that compare well with the 3H singlets seen experimentally, all predicted below 1.5 ppm and observed below 1.4 ppm experimentally. Also in the same region is a single proton signal, although its position is not predicted exactly. At the other end of the spectrum, there is a deshielded proton predicted at 5.15 ppm for the alkene proton. Attached to an alkene, this proton should be expected to be deshielded. There is a proton at 4.84 ppm experimentally. While the central group of fourteen proton shifts described in the literature agrees with the prediction, the doublet of doublets at 2.99 ppm adjacent to a group of four more deshielded protons is not seen as a result of calculations; a group of five protons is noted instead. Nonetheless, considering that the B3LYP/6-31Gdp model chemistry is a compromise between accuracy and computational expense, the prediction appears to be reasonably close to experiment.
The corrected 'O-down' isomer
The optimised structure of the corrected 'O-down' isomer 18 shown here is shown in below with atom numbering.

Averaging the chemical shifts for the freely rotating methyl groups again, the table below shows the predicted chemical shifts for isomer 18.
| Chemical shift /ppm | Proton number |
|---|---|
| 5.46 | 21 |
| 3.22 | 46 |
| 3.09 | 47 |
| 2.92 | 48, 49 |
| 2.78 | 22 |
| 2.68 | 30 |
| 2.63 | 27 |
| 2.48 | 25 |
| 2.36 | 36, 37 |
| 2.19 | 20 |
| 2.00 | 26, 19 |
| 1.87 | 24 |
| 1.76 | 31, 32, 33 |
| 1.54 | 23, 35 |
| 1.44 | 51, 52, 53 |
| 1.27 | 34 |
| 1.24 | 41, 42, 43 |
| 1.16 | 38, 39, 40 |
Listing in matching groups where possible and comparing as before:
1H NMR (predicted, C6D6) chemical shift 5.46 (1H), 3.22-2.68 (m, 6H), 2.63-2.36 (m, 4H), 2.19-1.76 (m, 7H), 1.54 (2H), 1.44 (s, 3H, Me), 1.27 (1H), 1.24 (s, 3H, Me), 1.16 (s, 3H, Me),
(lit.[1], 1H NMR (300 MHz, C6D6) chemical shift 5.21 (m, 1H), 3.00-2.70 (m, 6H), 2.70-2.35 (m, 4H), 2.20-1.70 (m, 6H), 1.58 (t, J = 5.4 Hz, 1H), 1.50-1.20 (m, 3H), 1.10 (s, 3H), 1.07 (s, 3H), 1.03 (s, 3H)).
Three methyl 3H triplets and a 1H signal are predicted below 1.5 ppm, agreeing roughly with the literature signal patterns and shifts for both isomers 17 and 18. The chemical shift for a single proton observed experimentally at 5.21 ppm agrees with that calculated here for the 'O-down' isomer 18 (5.46 ppm) but the most deshielded proton predicted for the 'O-up' isomer 17 5.15 ppm also agrees with this. When the remaining chemical shifts are put into groups, the predicted pattern for 18 (1H, 6H, 4H, 7H, 2H, 3H, 1H, 3H, 3H) can be taken to fit the experimental pattern for 18 (1H, 6H, 4H, 6H, 1H, 3H, 3H, 3H, 3H) approximately. Compare the pattern predicted for 17 (1H, 5H, 14H, 1H, 3H, 3H, 3H) with the pattern reported experimentally for 18, and the approximate fit in this case too could leave doubts about the assignment of the spectra to the isomers. Note that the experimentally determined spectrum reported for isomer 17 (1H, 4H, 1H, 14H, 3H, 3H, 3H, 1H) could also be made to appear to fit the data predicted for isomer 18 with a little regrouping. Comparing the chemical shifts of the peaks, either of the predicted spectra could be taken to match either of the experimental proton spectra roughly equally well given the correct prediction of the alkene proton to be deshielded in both predictions and the methyl groups to be deshielded, with variation in both cases as to the location of the singlet nearest to the methyl groups in the spectrum. A look at the splitting pattern, with coupling constants reported in Hertz by the experimenters, could be useful in making spectral assignments.
Coupling constants
Two new jobs have been submitted to the 'Gaussian - 8px' application in the HPC suite: calculations of the spin-spin coupling constants for isomers 17 and 18. The command lines differ in the solvent used for the simulation, and are as follows. For 17:
%chk=C:\G09W\Scratch\20140226 O-up 17 nmr freq all-couplings B3LYP 6-31Gdp.chk
# nmr=(giao,spinspin,mixed) b3lyp/6-31g(d,p) scrf=(cpcm,solvent=chloroform) geom=connectivity freq empiricaldispersion=gd3
For 18:
%chk=C:\G09W\Scratch\20140226 O-down 18 nmr freq all-couplings benz B3LYP 6-31Gdp.chk
# nmr=(giao,spinspin,mixed) b3lyp/6-31g(d,p) scrf=(cpcm,solvent=benzene) geom=connectivity freq empiricaldispersion=gd3
Both calculations ran for a minute or two on the desktop computer without problems, so the predictions will hopefully be ready for inspection tomorrow. In the mean Normal 0 false false false EN-GB X-NONE X-NONE time, it would be interesting to get to know the program ChemBio3D.
Modelling cyclopentadiene dimers
This product of the dimerisation reaction of cyclopentadiene was drawn in ChemDraw Pro 13.0 and loaded in ChemBio3D Ultra 13.0. This cyclopentadiene dimer with a trans ring junction was immediately displayed without any questions asked (Avogadro asks first if the structure should be made three-dimensional). Moving atoms and optimising several times at the MMFF94 level of theory produced this exo cycloaddition product 1 (with an energy of 55.3774 kcal/mol) and this endo reaction product 2 (with an energy of 58.1914 kcal/mol). While the process seemed simple enough, each optimisation resulted in a product with slightly lower energy than before. Avogadro will continue optimisation indefinitely, showing when the rate of change of potential energy has reached zero so that it is possible to know for sure when the energy minimum has been located. Preferring Avogadro's perpetual force optimiser, I will work with Avogadro from now. This will allow me to recalculate at the MMFF94s level. It appears at this stage that the exo isomer 1 is more stable, implying that this pericyclic reaction is under kinetic control (since the less thermodynamically stable endo isomer 2 is formed exclusively in reactions).
Optimising the endo isomer 2 in Avogadro (version 1.1.1) at the MMFF94s level of theory gave this structure of energy 58.19069 kcal/mol. The components contributing to the energy are shown in the table below.
| Energy type | Energy /(kcal/mol) |
|---|---|
| TOTAL BOND STRETCHING ENERGY | 3.46740 |
| TOTAL ANGLE BENDING ENERGY | 33.19104 |
| TOTAL STRETCH BENDING ENERGY | -2.08217 |
| TOTAL TORSIONAL ENERGY | -2.94985 |
| TOTAL OUT-OF-PLANE BENDING ENERGY | 0.02196 |
| TOTAL VAN DER WAALS ENERGY | 12.35756 |
| TOTAL ELECTROSTATIC ENERGY | 14.18475 |
| TOTAL ENERGY | 58.19069 |
Optimising the exo isomer 1 in Avogadro at the MMFF94s level of theory gave this structure of energy 55.37344 kcal/mol, agreeing with ChemBio3D that this isomer is lowest in energy. (Both approaches should agree: MMFF94 and MMFF94s model chemistries are both mechanical force fields.) Component energies are shown below.
| Energy type | Energy /(kcal/mol) |
|---|---|
| TOTAL BOND STRETCHING ENERGY | 3.54300 |
| TOTAL ANGLE BENDING ENERGY | 30.77270 |
| TOTAL STRETCH BENDING ENERGY | -2.04139 |
| TOTAL TORSIONAL ENERGY | -2.73103 |
| TOTAL OUT-OF-PLANE BENDING ENERGY | 0.01485 |
| TOTAL VAN DER WAALS ENERGY | 12.80163 |
| TOTAL ELECTROSTATIC ENERGY | 13.01367 |
| TOTAL ENERGY | 55.37344 |
Comparing the components of the total energy for the isomers, it appears that although the van der Waals energy is slightly higher for the exo isomer 1, raising its energy, this is more than compensated for by the reduced angle bending energy and, to a lesser extent, electrostatic energy relative to the endo isomer 2. It appears that the exo isomer has less ring strain.
Modelling the hydrogenated cyclopentadiene dimers
Investigating the possible products from the hydrogenation of the endo cyclopentadiene dimer 2, note that there are two conformers of isomer 3. This conformer is the higher-energy conformer, with an energy of 50.72284 kcal/mol.
The table below shows the component energies of the lower energy (50.44568 kcal/mol) conformer of 3 shown here. This conformer is presumably lower in energy because the hydrogenated side of the molecule points away from the double bond.
| Energy type | Energy /(kcal/mol) |
|---|---|
| TOTAL BOND STRETCHING ENERGY | 3.31141 |
| TOTAL ANGLE BENDING ENERGY | 31.93584 |
| TOTAL STRETCH BENDING ENERGY | -2.10216 |
| TOTAL TORSIONAL ENERGY | -1.46979 |
| TOTAL OUT-OF-PLANE BENDING ENERGY | 0.01319 |
| TOTAL VAN DER WAALS ENERGY | 13.63767 |
| TOTAL ELECTROSTATIC ENERGY | 5.11951 |
| TOTAL ENERGY | 50.44568 |
The other hydrogenated isomer 4 has an energy of only 41.25749 kcal/mol. With no other conformers with lower energies that the simulation could find, this isomer would be the one expected to form under thermodynamic conditions. (This does not say anything, however, about the energetic level of the transition state and kinetics, so without this information, it could be assumed that this isomer 4 is indeed the one expected to be most likely to form.) For comparison, the components of the total energy of this molecule are shown in the table below.
| Energy type | Energy /(kcal/mol) |
|---|---|
| TOTAL BOND STRETCHING ENERGY | 2.82307 |
| TOTAL ANGLE BENDING ENERGY | 24.68545 |
| TOTAL STRETCH BENDING ENERGY | -1.65716 |
| TOTAL TORSIONAL ENERGY | -0.37821 |
| TOTAL OUT-OF-PLANE BENDING ENERGY | 0.00028 |
| TOTAL VAN DER WAALS ENERGY | 10.63703 |
| TOTAL ELECTROSTATIC ENERGY | 5.14702 |
| TOTAL ENERGY | 41.25749 |
Every component of the energy, except for the electrostatic energy, is lower. The release of ring strain in the bicyclic system seems to want to drive the hydrogenation reaction strongly.
Since both isomers 3 and 4 have energies lower than the starting endo dimer 2, under equilibrating conditions both would be expected to form to some degree (this assumes that there are no kinetic barriers to their formation), with low-energy isomer 4 forming a larger proportion of the product.
Carbon NMR and coupling constants for the taxol precursors
20140227 Thursday
Last night's calculations of the spin-spin coupling constants of 'O-up' isomer 17 and 'O-down' isomer 18 of the taxol synthetic precursor took 6 hours 17 minutes and 6 hours 14 minutes respectively on the 'Gaussian - 8px' application of the HPC suite - both really big calculations on structures that were already structurally optimised at the B3LYP/6-31Gdp level used for the calculations. Without knowing how to inspect the coupling constants just yet, the carbon NMR spectra will be examined below and compared to the literature findings.
Carbon NMR for the isomers
The predicted proton NMR spectrum in deuterated chloroform is shown below for isomer 17.

While some of the protons in this spectrum needed averaging due to their presence on freely rotating methyl groups, this does not apply to the carbon NMR predicted spectrum (in chloroform) shown below for the same isomer 17.

Carbon chemical shifts are listed in the table below.
| Chemical shift /ppm | Carbon number |
|---|---|
| 216.18 | 14 |
| 145.12 | 2 |
| 124.80 | 3 |
| 90.49 | 10 |
| 60.66 | 9 |
| 57.13 | 8 |
| 52.60 | 6 |
| 51.68 | 7 |
| 46.80 | 4 |
| 46.03 | 44 |
| 42.28 | 11 |
| 40.55 | 45 |
| 35.43 | 15 |
| 31.26 | 5 |
| 29.42 | 13 |
| 29.37 | 50 |
| 27.30 | 1 |
| 26.43 | 16 |
| 23.01 | 12 |
| 19.82 | 17 |
As should be expected, the unsaturated carbons are most deshielded, with the carbonyl carbon most deshielded of all followed by the alkene carbons.... but without further ado, this is the same pattern seen in both the other isomer, 18, and both literature molecules, so without being able to conclude very much from a carbon NMR analysis, the coupling constants will be looked at.
The predicted proton NMR spectrum in deuterated benzene is shown below for the 'O-down' isomer 18.

The predicted carbon NMR spectrum for the 'O-down' isomer 18 (in benzene) is shown here in graph form and tabulated:

| Chemical shift /ppm | Carbon number |
|---|---|
| 209.04 | 14 |
| 148.81 | 2 |
| 118.64 | 3 |
| 91.24 | 10 |
| 64.49 | 9 |
| 55.36 | 6 |
| 54.62 | 8 |
| 50.05 | 7 |
| 45.63 | 45 |
| 41.74 | 44 |
| 37.80 | 11 |
| 37.55 | 4 |
| 35.57 | 13 |
| 34.20 | 15 |
| 32.18 | 50 |
| 28.63 | 1 |
| 26.22 | 16 |
| 25.15 | 5 |
| 22.81 | 17 |
| 22.31 | 12 |
The patterns, while fitting the experimental data reasonably well, are both so similar that they should not be considered too deeply, although it should be noted that the range of chemical shifts agrees with the literature,[1] with the smaller range of shifts (from most deshielded to least deshielded) occurring for isomer 18 in both cases. This is positive evidence of the correct assignment.
Coupling constants for selected protons
Paqette, Pegg, Toops, Maynard, and Rogers (1990) reported several coupling constants for the proton NMR peaks.[1] The total nuclear spin-spin coupling, J (in Hz), is reported in the Gaussian log file for each pair of nuclei.
Assuming coupling between only the closest non-equivalent protons to be significant, the first peak to look at here will be the doublet of doublets seen at 4.84 ppm (J = 7.2, 4.7 Hz) for the 'O-up' isomer 17. This is the alkene proton, the most deshielded proton in the molecule, the peak predicted for proton number 21. This peak is reported at 5.21 ppm as a multiplet for the 'O-down' isomer 18, so there is a difference to investigate. This proton, in both isomers, couples with the nearest protons 19, 20, 36 and 37, all four bonds away. Protons numbered 19 and 20 could be predicted to give the greater coupling magnitudes because they couple through a double bond, with correspondingly higher s-core electron character in the bonds through which they communicate with proton 21.
For the 'O-up' isomer 17, the total nuclear spin-spin coupling J values shown in the log file are:
19 to 21: -0.321669D+01 Hz = -3.2 Hz
20 to 21: -0.158738D+01 Hz = -1.5 Hz
21 to 36: 0.558876D+01 Hz = 5.6 Hz
21 to 37: 0.126009D+02 Hz = 12.6 Hz
For the 'O-down' isomer 18, the total nuclear spin-spin coupling J values shown in the log file are:
19 to 21: -0.310729D+01 Hz = -3.1 Hz
20 to 21: -0.168527D+01 Hz = -1.7 Hz
21 to 36: 0.348312D+01 Hz = 3.5 Hz
21 to 37: 0.123011D+02 Hz = 12.3 Hz
Transition state analysis for the cyclodimerisation
It was assumed earlier that because the thermodynamically favourable isomer of the cyclodimerisation of cyclopentadiene is not formed, the reaction must be under kinetic control. Calculating the energies of the transition states should give conformation that the least thermodynamically stable endo isomer 2 has a lower energy transition state and should therefore be the kinetically favoured product.
Adapting the exo product 2 by drawing dotted lines to indicate 'half bonds' between the two cyclopentadiene halves of the molecule, and moving the two halves apart a little, this exo transition state was obtained. Optimised to a Berny transition state, calculating force constants once and using 'opt=noeigen' to stop the calculation terminating prematurely, this transition state was calculated at the HF/3-21G level in Gaussian. The energy of this structure is -383.38354481 a.u.. The transition state has one imaginary frequency, as expected for an energy maximum, at -719.17 /cm, corresponding, as shown in the picture below (clicking on the image will give a larger animated image) to the two halves coming together, just as required for this transition state.

Treating the endo product 1 in the same way, this HF/3-21G endo transition state was obtained. The structure has an energy of -383.38600018 a.u.. The imaginary frequency (only one as required for an energy maximum, -651.45 /cm) is animated below. It corresponds, correctly, to the cyclopentadiene monomers coming together.

The transition structure of dimer 1 is lower in energy than that of dimer 2 (by 0.00245537 a.u.) when using like-for-like computational calculations with the HF/3-21G model chemistry using the same program: the energies are directly comparable. This confirms that the endo product 1 will form more quickly, with less activation energy required for reaction then the thermodynamically more stable dimer 2. A look at the electron distribution in the molecule may give a clue about the stability of the transition state.
Molecular orbitals explain the reactivity
The endo transition state on the path to the formation of endo dimer 1 allows the close apposition of the reacting double bond systems, including the parts of these that do not directly react together to form bonds. The highest occupied molecular orbital (HOMO) can be seen to span between these double bonds in a bonding interaction (a single lobe with no nodes). The orbitals (for both transition states) are shown below. The models are interactive and can be manipulated (enlarged, rotated) by the reader.
Endo transition state highest occupied molecular orbital
Endo HOMO |
Exo transition state highest occupied molecular orbital
Exo HOMO |
The transition state belonging to the exo dimer 2 does not have supportive bonding interactions between the forming double bonds of the system, because they are far apart. These orbitals are higher in energy, illustrating graphically why the endo product 2 forms more quickly through the more stable of the two transition states.
Atropisomerism in the taxol derivatives
20140228 Friday
The height of the activation barrier between two atropisomers might explain why their interconversion is slow. Returning to the very first structures generated on Saturday, optimising the structures this time at the MMFF94s level generated these two structures: this 'O-up' isomer 9 of energy 70.53911 kcal/mol and this 'O-down' isomer 10 of energy 68.87690 kcal/mol. Isomer 10, here with a boat conformation in its six-membered ring, is more stable by 1.66 kcal/mol, but this says nothing about the rate of the reaction. For this, an examination of the transition state should be needed.... hang on... the conformation of the six-membered ring also affects the energy. This newly found conformer of 10 with the oxygen 'down' and a tweaked six-membered ring chair conformation has an energy of 60.55146 kcal/mol, very much lower in energy than those conformers found previously. This conformation gives the carbonyl group plenty of room. I bet that the isomerisation between 'O-up' and 'O-down' forms is relatively slow because the six-membered ring must also change conformations at the same time... Yes. Trying to enforce the same chair conformation in the six-membered ring structure of the 'O-up' isomer by switching on the perpetual force optimiser of Avogadro and moving the oxygen from the 'down' to the 'up' position without changing the six-membered ring conformation leads to this very high energy conformer ('O-up' with an energy of 87.74304 kcal/mol). To relax again, the 'O-up' conformer then moves through this boat form of an intermediate energy (76.28966 kcal/mol) before reaching its final resting point, this stable chair form of energy 70.53838 kcal/mol. The sequence of events (which I did not consider in structures of taxol derivatives used to predict NMR spectra) could be, with a couple of extra conformers to complete the ring-flipping cycle:
Stable chair form of 'O-up' 9 (70.54 kcal/mol, view here)
Stable boat form of 'O-up' 9 (76.29 kcal/mol, view here)
Unstable boat form of 'O-up' 9 (88.17 kcal/mol, view here)
Unstable chair form of 'O-up' 9 (82.74 kcal/mol, view here)
Stable chair form of 'O-down' 10 (60.55 kcal/mol, view here)
Stable boat form of 'O-down' 10 (68.87690 kcal/mol, view here)
Unstable boat form of 'O-down' 10 (81.53 kcal/mol, view here)
Unstable chair form of 'O-down' 10 (74.76 kcal/mol, view here)
Stable chair form of 'O-up' 9 (70.54 kcal/mol, again...)
The chair forms are more stable than their adjacent boat forms. Underlying this, the 'O-up' isomer 9 really does not like to be in the wrong chair form, exactly the opposite chair conformation to that which is most energetically favourable for the 'O-down' isomer 9 to be in. The converse is also true. In fact, considering this, I would like suggest a revised most likely sequence of events.
The above sequence has the oxygen moving from the 'up' to the 'down' position in a way that involves the very high energy conformations where the molecule has the wrong chair form-oxygen position combination. A lower-energy pathway to the isomerisation would likely be for the oxygen to change from 'up' to 'down' between the chair forms:
Stable chair form of 'O-up' 9 (70.54 kcal/mol, view here)
Stable boat form of 'O-up' 9 (76.29 kcal/mol, view here)
(Inversion of the carbonyl group at this point)
Stable boat form of 'O-down' 10 (68.87690 kcal/mol, view here)
Stable chair form of 'O-down' 10 (60.55 kcal/mol, view here)
The cycle then goes back the way it came if energy is available (the high-energy conformers are avoided).
Most of the molecules will be in one of the stable chair conformations in any equilibrium population, since these are lowest in energy (the equation delta G = RT ln K applies). I must look at my NMR calculations again to see if, by chance, I had hit upon the correct low-energy structures that represent the major conformer present in the NMR sample tube: if not, I will have to calculate again.
Optimising structures at the HF/3-21G level of theory, a transition state was located using the QST3 method with the 'O-up' isomer as the starting material and the 'O-down' isomer, with identical atom numbering, as the product.
Transition state for the isomerisation
20140301 Saturday
The QST3 method for finding a transition state allows for the input of not only a starting point and an end point, but also a guess at the structure of the transition state itself, a middle point. For this, the oxygen atom of the carbonyl group was moved, in Avogadro's perpetual force optimiser, so that the carbonyl group was teetering between the 'up' and 'down' positions, in a 'sideways' orientation as shown here (102 kcal/mol; note that since an estimate of the available energy at room temperature, kT, is only 0.6 kcal/mol, the higher-energy conformers - let alone the transition state - of these isomers are unlikely to be accessible without heating).
The HF/3-21G model chemistry predicted a QST3 transition state where the only imaginary vibration was a rotating motion of the methyl group nearest to the oxygen atom. A calculation at the B3LYP/6-31G* level (choosing B3LYP/6-31d as the basis set) on the same input structures was more successful, finding the transition state between stable chair form and stable boat form of the 'O-up' isomer. The animation for this is shown below. The transition state, however, does not shed light on the inversion of the carbonyl group.

Returning to the earlier NMR studies
Thinking again about the sulphur-containing taxol derivatives, 17 and 18, showing the following coupling constants to the alkene proton (proton number 21):
For the 'O-up' isomer 17:
19 to 21: -3.2 Hz
20 to 21: -1.5 Hz
21 to 36: 5.6 Hz
21 to 37: 12.6 Hz
For the 'O-down' isomer 18:
19 to 21: -3.1 Hz
20 to 21: -1.7 Hz
21 to 36: 3.5 Hz
21 to 37: 12.3 Hz
Something looks wrong, because although one isomer was reported to show a multiplet for the alkene proton's signal, the other isomer is reported as a doublet of doublets. This is not what should be expected from these rather similar predicted splitting patterns. The conformers analysed were not both the most stable isomers. Because of this the studies did not represent the majorities of the populations. The 'O-up' sulphur-containing isomer 17 appears fortunately to be in its most stable form, with the ring junction matching the conformation of the stable chair form of 'O-up' isomer 9. The 'O-down' sulphur-containing taxol synthetic precursor 18 has a six-membered ring in its boat form, when the chair form of 'O-down' isomer 10 is now known to be lowest energy. The wrongly-calculated conformer of 17 should only represent a small fraction of this isomer in the NMR tube. The six-membered ring suffers from eclipsed conformations around the ring.
Opening the stable boat conformer of the 'O-down' isomer 18 upon which the NMR calculations were performed in Avogadro and optimising at the MMFF94s level gave a structure of energy 102.31362 kcal/mol. Moving the atoms around to put the molecule in its stable chair form, the new molecule has an energy of 100.44074 kcal/mol (a difference of roughly three times the thermal energy at room temperature, kT). This includes the sulphur-containing ring in its lowest-energy form (in its slightly higher-energy form, the structure has an energy of 100.49391 kcal/mol in this force field model; since this is only 0.053 kcal/mol higher in energy, compared to kT = 0.6 kcal/mol at room temperature, it can be assumed that the carbons between the sulphur atoms in the ring wobble around freely at room temperature).
Since the new 'O-down' chair conformation changes the position of the plane of the double bond, the splitting pattern of the alkene proton may change too.
For comparison, moving the new 'O-down' chair isomer 18 from Avogadro around to make it into the 'O-up' most-stable chair conformation of isomer 17 gives a structure of energy 104.30987 kcal/mol. This is roughly a further three room-temperature thermal energies higher in energy than the stable boat form of the 'O-up' isomer. For further comparison, the least stable 'O-up' boat form has an energy of 127.08287 kcal/mol, the 'O-up' more stable boat form an energy of 120.49570 kcal/mol and the 'O-up' unstable chair form an energy of 117.94480 kcal/mol. While this is the same pattern seen with isomers 9 and 10, energies of two molecules that are not isomers are not comparable using Avogadro.
Epoxidation reactions
Some calculations set up to run overnight have given predicted spectra for the epoxides.
Predicted NMR spectra for the epoxides
The NMR spectra were all calculated following the same procedure. The structure of the epoxide was first drawn in ChemdrawPro 13.0 then optimised at the MMFF94s level in Avogadro. The structures produced were further optimised at the HF/3-21G level in Gaussian and checked to confirm absence of imaginary frequencies. They were then optimised again at the B3LYP/6-31Gdp level and again checked to confirm absence of imaginary frequencies following the optimisations. The spin-spin coupling for all atoms was then computed for each epoxide at the B3LYp/6-31Gdp level using the computing power of the HPC suite. With chloroform solvent, setting EmpiricalDispersion=GD3, an example command line is shown below.
%chk=C:\G09W\Scratch\20140227 Styrene Ox B3LYP 6-31Gdp nmr s-s mixed chloro freq GD3.chk
# nmr=(giao,spinspin,mixed) b3lyp/6-31g(d,p) scrf=(cpcm,solvent=chloroform) geom=connectivity empiricaldispersion=gd3 freq
Calculation times for styrene, methylstyrene, stilbene, and dihydronapthalene oxides were 16, 20, 49 and 29 minutes respectively (spin-spin couplings step only). The spectra were visualised using gNMR version 5.0.6.0 (set to 400 MHz). This program produced an output similar to that seen in experimental NMR printouts when the chemical shifts and coupling constants were input for each hydrogen atom.
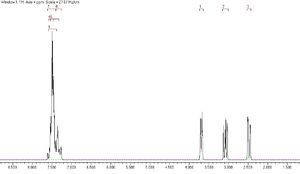
Styrene oxide
The predicted NMR for the epoxide styrene oxide is shown below. Numbering of the peaks, shown more clearly in the expansions, corresponds to that shown in the diagram.



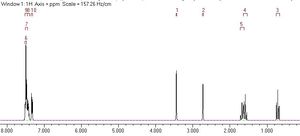
Methylstyrene oxide
The predicted NMR for beta-methylstyrene oxide at zero Kelvin is shown below. There seem to be too many peaks for a molecule with a rotating methyl group, but then, at absolute zero, the methyl group would not be rotating.



The methyl group protons' signals clearly need averaging. This is done by taking the mean chemical shift and giving all three protons the same mean chemical shift (1.324 ppm) in the gNMR spectrum predictor. The new room temperature predicted spectrum is shown below.



Stilbene oxide
The predicted NMR for stilbene oxide is shown below.



Dihydronapthalene oxide
Click to enlarge the expansions in the predicted NMR spectrum for the epoxide dihydronapthalene oxide below.



NMR analysis of the taxol synthetic precursors (continued)
20140302 Sunday
Having learned from studies of the atropisomers of the taxol synthetic precursors 9 and 10 that the lowest-energy conformations (those best representing the population of conformers in the NMR tube during sample acquisition) of sulphur-containing isomers 17 and 18 were those initially used for the NMR simulations, the predicted NMR data were recalculated. The lowest-energy conformations of 17 and 18 were used, conformations which I am now referring to as 'O-up S-up' and 'O-down S-down' in file names after the positions of the O and S atoms in these conformers. 'O-up S-down' and 'O-down S-up' conformations are higher in energy, representing the finding that for one atropisomer to rearrange into the other isomer, the inversion of the carbonyl group must be accompanied by ring-flipping in the six-membered ring (with corresponding change in the position of the attached sulphur-containing ring).
Recalculations of the predicted NMR data for the 17 and 18 were performed following the same procedure for the epoxides, with calculation times of 6 hours 17 minutes and 7 hours 26 minutes respectively. The energies of the calculated structures for 17 and 18 were -1651.88236696 a.u. and -1651.88337066 a.u. respectively.
The newly calculated predicted spectrum for the 'O-up' isomer 17 is the same as calculated before, as should be expected. It is the same conformer. This calculation, made using a newly optimised structure generated from the new 'O-down' isomer 18 by moving the atoms in Avogadro's perpetual force optimiser, can be used as a control when compared to the independently optimised previous 'O-up' isomer 17.)
A look at the coupling constants
20140303 Monday
Continuing with the procedure used for the epoxides, for the alkene proton and nearest neighbours, the coupling constants were entered into gNMR5 to generate peaks. First, a look at the newly calculated NMR data for isomer 17 as a control measure. While essentially the same as before, the data have very slight differences that show the calculation results are not set in stone.
'O-up S-up' isomer (control calculation)
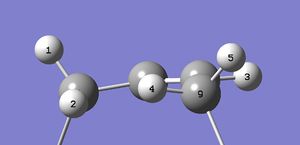
For isomer 17 in the low energy 'O-up S-up' conformation, shown here, the diagram below shows numbering for the protons used to generate the peak pattern also shown below for the alkene proton at 5.145 ppm.


Making the assumption that only the protons coupling through the double-bond system will be seen, (coupling between protons 2 and 3 and protons 3 and 4 only,) a somewhat simpler spectrum is predicted:

A doublet of doublets. In this assumption based on the Karplus relationship[2], coupling between protons the alkene proton (number 3) and in-plane protons 2 and 4 is strong. Coupling between and perpendicular protons 1 and 5 (both out of the plane containing protons 2, 3 and 4 and the joining carbon framework) is not seen. The alkene fragment below shows the geometries involved.
The total nuclear spin-spin coupling J values used are (with previously calculated coupling constants in parentheses for comparison as a control):
1 to 3: -0.323127D+01 = -3.23 Hz (previously 19 to 21: -0.321669D+01 Hz; not seen)
2 to 3: -0.159511D+01 = -1.60 Hz (previously 20 to 21: -0.158738D+01 Hz)
3 to 4: 0.126155D+02 = 12.62 Hz (previously 21 to 37: 0.126009D+02 Hz)
3 to 5: 0.559394D+01 = 5.59 Hz (previously 21 to 36: 0.558876D+01 Hz; not seen)
The coupling constants are very close but are, at the same time, slightly different. It is likely that a very slightly different minimum energy conformation was generated second time around, giving rise to slightly different couplings.
'O-down S-down' isomer (recalculated)
For isomer 18 now in its lowest-energy 'O-down S-down' conformation, here, numbering and generated alkene peak at 5.965 ppm are shown below. This proton's relatively deshielded position (compared to the same proton in isomer 17) is in agreement with the literature in this respect, (although literature shifts are both somewhat less than the predicted shifts).


The geometry of the main population of this 'O-down' isomer, 18, around the alkene, is different from that of 18: now the carbon adjacent to the six-membered ring is rotated by ten degrees, so that protons 4 and 5 are both slightly out of the plane of the alkene system yet not perpendicular to it. Assuming now that only proton number 1 does not couple with the alkene proton 3, a multiplet is seen:

Not a doublet of doublets. The detail of the geometry in the alkene fragment is shown below.

The total nuclear spin-spin coupling J values used are:
1 to 3: -0.337836D+01 = -3.38 Hz (not seen)
2 to 3: -0.186172D+01 = -1.87 Hz
3 to 4: 0.128238D+02 = 12.82 Hz
3 to 5: 0.649448D+01 = 6.49 Hz
The change of geometry all the way around the largest ring system, from the inverted carbonyl group, through the flipped six-membered ring, to the alkene system, is reminiscent of enzyme structural changes at the active site when a modulator binds at a distant allosteric site. Regarding the assignment of the NMR spectra to isomers 17 and 18, the geometric changes at the alkene upon isomerisation give rise to different populations in the NMR tubes of the separate isomers. Interconversion is slow, so pure samples could be obtained for long enough to run an NMR experiment: the multiplet observed in the alkene peak for 18 can be explained without suggesting that the sample was impure. Calculations confirm that 18 is the lowest-energy isomer, to which all of 17 will convert in time. The change in geometry shown in the computed structures explains, through the Karplus relationship, how a proton rotating into the plane of the alkene system gains a great enough coupling to turn a doublet of doublets (reported for isomer 17) into a more complex multiplet. It appears that the spectra were indeed assigned correctly.
Before trying to place the peaks in the predicted spectra of 17 and 18 into groups to match the experimentally observed spectra these isomers, the peak observed for isomer 18 at 1.58 ppm should be considered. This 1H triplet has a reported 5.4 Hz coupling.[1] The full zero Kelvin predicted proton spectrum for 17 in deuterated chloroform is shown below:

The predicted zero Kelvin spectrum for 18 in deuterated benzene is shown below:

At first glance, there is no isolated peak in either of the spectra at 1.58 ppm that could be attributed to one single proton. These spectra do not take into account the free rotation of the methyl groups at room temperature. Averaging the peaks for the three groups of protons, (38,39,40), (41,42,43) and (51,52,53) by taking the means as before, however, fixes this. For the 'O-down S-down' isomer 18, averaging the methyl protons' signals gives the following set of peaks (grouping with a degeneracy tolerance of 0.05 ppm):
| Chemical shift /ppm | Proton number |
|---|---|
| 5.97 | 21 |
| 3.11 | 46, 48 |
| 2.97 | 37, 49 |
| 2.86 | 36, 47 |
| 2.77 | 22 |
| 2.69 | 20 |
| 2.55 | 25, 27 |
| 2.42 | 32 |
| 2.30 | 30 |
| 1.99 | 19, 26 |
| 1.84 | 24, 31 |
| 1.58 | 23 |
| 1.50 | 34 |
| 1.37 | 51, 52, 53 |
| 1.33 | 33 |
| 1.26 | 41, 42, 43 |
| 1.22 | 35 |
| 1.17 | 38, 39, 40 |
Proton numbers can be seen by clicking to view the molecule here and selecting Style > Labels > With Atom Number from the menu. Proton number 23 at 1.58 ppm is not a triplet but an overlapping doublet of doublets: this proton can now be seen to couple with both the geminal proton (22) and the vicinal proton (26) with coincidental J values giving rise to a triplet. As listed above, there is no single proton peak at 1.58 ppm for isomer 17. The nearest peak is a pair of protons at 1.60 ppm. This is further evidence of the correct assignment of the spectra to the isomers in the literature examined here.
Grouping the chemical shifts and comparing as before:
1H NMR (predicted, C6D6) chemical shift 5.97 (1H), 3.11-2.86 (m, 6H), 2.77-2.55 (m, 4H), 2.42-1.84 (m, 6H), 1.58 (dd, 1H), 1.50 (1H), 1.37 (s, 3H, Me), 1.33 (1H), 1.26 (s, 3H, Me), 1.22 (1H), 1.17 (s, 3H, Me),
(lit.[1], 1H NMR (300 MHz, C6D6) chemical shift 5.21 (m, 1H), 3.00-2.70 (m, 6H), 2.70-2.35 (m, 4H), 2.20-1.70 (m, 6H), 1.58 (t, J = 5.4 Hz, 1H), 1.50-1.20 (m, 3H), 1.10 (s, 3H), 1.07 (s, 3H), 1.03 (s, 3H)).
The comparison seems to look a little better than before, but these protons have really been forced into groups to match the literature and still the 3H multiplet observed experimentally at 1.50-1.20 ppm is nowhere to be seen in the prediction (instead there are rather spread out 1H signals superimposed on the methyl group 3H singlets).
The predicted carbon NMR shifts for 17 are shown below:

For 'O-down S-down' isomer 18:

Considering the accuracy of predictions of the chemical proton shifts, little evidence of the correct assignment of the spectra to a particular isomer can be taken from these carbon NMR predictions. Both spectra are very similar. Any correspondence with experiment would feel coincidental.
Initial conclusions
20140304 Tuesday
Before moving on to investigate the catalysed epoxidation reactions further, first a look back at what has been learned so far.
Reproducibility of the calculations
Having made the mistake of launching into expensive calculations of NMR data on one of the less stable conformers, one not representing the largest proportion of conformers in an experimental NMR tube, the calculations were repeated for both the previously wrong conformer of 18 but also for the correct conformer of 17 as a control calculation. The conformation of configuration 17 modelled initially had an energy of -1651.88240695 a.u. and the same conformer of 17 when calculated second time had an energy of -1651.88236696 a.u., a difference of 0.00003999 a.u. or 0.025 kcal/mol. While this is a very small difference, it suggests that performing the same calculation twice independently will result in slightly different conformations of the molecule at the minimum energy conformation. There were small differences in the NMR spin-spin coupling constants, too, although the pattern of chemical shifts is comparable. The calculations are reproducible within small tolerances.
Avogadro's perpetual force optimiser
It was all too easy to jump ahead to NMR studies without looking at energies of the interconverting atropisomers. Avogadro's perpetual force optimiser, using the MMFF94s force field, proved a quick and engaging method of looking at the energies associated with ring flipping and inversion of the carbonyl group. It was easy to pull around the atoms to new conformations to find the lowest energy conformers. Learning the lesson, it is important to do this prior to NMR studies to locate the lowest energy conformations because these conformations represent the population of molecules in the NMR tube.
Predicted chemical shifts
It was seen that the predicted chemical shifts of a slightly higher energy conformation of 18 were very different from the lowest energy conformation of 18 upon recalculation. Since the molecule is always in motion at room temperature, it might be expected that the experimentally determined NMR spectrum should be skewed from that expected for the lowest energy conformer to that of the 'nearest' low-energy conformer. This might explain the differences between calculated chemical shift and experimental observation (the stability of chemical shifts between duplicated calculations on configuration 17 is enough that random variation in the predicted spectral peaks is not the explanation). The conformations, changing with thermal motion, of the molecule will each have a different geometry and a different NMR spectrum. What is actually seen is an average of these. One is likely not enough.
To deal with the effects of molecular motion on a predicted NMR spectrum calculated at zero Kelvin, the predicted signals for the different methyl group protons were averaged to simulate free rotation of these groups. If the rotation of the groups was not completely free, it could be expected that taking a mean average could lead to inaccuracies since one conformation would be favoured. The methyl group signals, 3H singlets, however, compared well with experimental observations: in that they were in the right part of the spectrum. The carbon NMR spectrum was little use in assigning the configurations, considering the similarity of the predicted spectral pattern and the sensitivity of the chemical shifts to small changes in geometry.
Predicted coupling constants
If the calculations were predicting the correct coupling constant parameters, they might not have been being used correctly. It appeared from the tables of total spin-spin coupling constants generated by Gaussian that the Karplus equation was not automatically applied to give a set of realistic coupling constants, as seen in an examination of the alkene proton's splitting pattern. This might make sense considering that the Karplus relationship can be modelled in more than one way. Thus the user is free to use the Gaussian output in the desired way. The way that Gaussian allowed the visualisation of bond twisting in relation to the alkene proton, allowing inference of the effects of conformational change on spectral splitting patterns, was very impressive. A ten degree change in dihedral angle was clearly seen, reminiscent of structural changes in distant parts of an enzyme upon binding of a ligand.
Rationalisation of reactivity
The great advantage of using Gaussian over Avogadro is the molecular orbital approach. The B3LYP/6-31G* model chemistry allowed the visualisation of the orbital interactions in reacting cyclopentadiene monomers, showing visually the stabilisation afforded by the endo configuration in cycloaddition reactions. This was wonderful to see. The bonding-type interactions were clearly pulling down the height of the potential barrier to reaction by the endo pathway compared to the exo pathway, overcoming the thermodynamic stability of the exo product. Could similar interactions explain the greater stability of configuration 18 of the taxol synthetic precursor? Below, the HOMO for this isomer shows few significant interactions of this kind.
Endo HOMO |
Could there be attractive van der Walls' interactions between the protons of the methyl and methylene groups on one face of the molecule? Johnson, Keinan, Mori-Sánchez, Contreras-García, Cohen and Yang (2010) created revealing images of these interactions.[3] Plotting the non-covalent interactions in a similar way:
Endo HOMO |
There are lots of non-covalent interactions, attractive with the exception of the interaction (red) in the centre of the five-membered rings. For comparison, non-covalent interactions in the lowest energy conformation of 17 are shown below.
Endo HOMO |
While this structure also has many non-covalent interactions, the attractive interactions do not extend throughout the centre of the largest ring. Perhaps this could be the explanation of the lower stability of configuration 18.
The results of the last calculations of NMR data for the 'O-up S-up' conformer of 17 investigated here can be accessed at DOI:10042/27771 . The calculated NMR output for the 'O-down S-down' conformer of configuration 18 is at DOI:10042/27772 .
Predicting the reactivity of the Jacobson epoxidation of stilbene
20140306
After two days wondering about the transition states, wondering whether it is possible to tell by looking at the catalysts and the substrates which will react fastest - whether it would be possible to use molecular modelling to design a catalyst that will impart its own chirality on a reactant to make a product of the right stereochemistry itself - a picture of the molecules seems to have become clear. Instead of looking at a picture with no features...





...now it seems that the transition states viewed not only each hold a different forming epoxide enantiomer: each transition state suffers a different balance of destabilising against stabilising interactions. The forming (R,R) enantiomer on the right in the images below appears to suffer greater steric clash with the Jacobsen catalyst than the forming (S,S) enantiomer to the left.




There is an attractive pi-pi stacking pulling the stilbene into the catalyst and at the same time, in the precise orientation for the epoxidation reaction to occur and at that moment, there is a steric 'push' of the stilbene back down on the bulky alkyl chain (which can not revolve out of the way) of the catalyst. The six-membered chair of the catalyst's ligand is fused in place by the coordination of the metal. It can not ring flip. The result of the fusion of the ring, as with the 'O-up' and 'O-down' configurations of the taxol synthetic precursor studied above, has a knock-on effect elsewhere in the molecule. In the present case, the result is that the push of the forming enantiomer of stilbene oxide distorts the nitrogen-oxygen chelating ring of the ligand around the metal centre more for the forming (S,S) enantiomer. This is shown in the last of the images above, where the magnitude of the N-N-O-O dihedral angle in the (S,S) transition state is 24.0 degrees (bottom left corner; click the image to enlarge) whereas it is 9.9 degrees in the (R,R) transition state. If the interpretation of steric push and pi-pi interaction is correct, this will likely show up in a non-covalent interactions study of the transition state - with slightly more of a clash in the region indicated above.
While it may intuitively feel that raising the overall energy of the system by distorting the plane of the ligand should raise the (S,S) transition state structure, kinetically favouring the formation of the (R,R) epoxide, would this be in line with the weakening of planar ligand field around the manganese ion allowing greater electron density to go to the oxygen atom being delivered to the stilbene? Greater bonding electron density into forming epoxide bond would favour its formation, so would greater anti-bonding electron density going into the forming epoxide bond disfavour its formation? Yamada (1999) notes in a review of the development of Schiff-base metal complexes that in one of the 'early versions' of the Jacobsen catalyst, cobalt-containing salcomine, the ligand field produced by its Schiff-base ligand, 'Salen', is so strong that the four-coordinate planar complex would have only a very limited capacity for bonding at the fifth and sixth coordination sites. [4] Bulky ligands, distorting the plane and weakening the grip of the Salen ligand on the metal centre, allowed more ready formation of five-coordinate systems. Perhaps the distorted plane of the (S,S) metal centre here could be reducing bonding electron density building up in the epoxide bond, 'double-disfavouring' the formation of the transition state - and of course kinetically favouring the (R,R) epoxide proportionally. The oxygen-carbon bond should be lower in energy than the transition metal centre, so allowing easier population of antibonding levels by the more 'relaxed', distorted metal centre.
Non-covalent interactions in the (R,R) transition state are shown below:
Endo HOMO |
For the (S,S) transition state, predicted to be disfavoured, non-covalent interactions are shown below:
Endo HOMO |
It seems that there is no steric clash after all. The stilbene strongly attracts itself (blue and green interactions, including where it was previously suggested there would be steric clash) to the catalyst in both cases. The only steric clash appears to be within ring structures, particularly the small rings held very tightly into the metal centre (red). The stilbene appears to distort the O-O-N-N plane of the catalyst by binding to it with non-covalent interactions. The lack of colouring around the forming and bond, however, suggests that some other kind of visualisation could be useful here.
Electronic topology study of the transition states
20140307 Friday
The quantum theory of 'atoms in molecules' (QTAIM) method[5] was applied to the transition states of the Jacobsen catalyst in Avogadro. The analysis shows both the expected interaction between the reacting central double bond of the alkene (it can react without disrupting the aromaticity of the phenyl groups on either side) and the oxygen bound to the metal ion outside the plane of the ligand, but also an interaction with the ligand itself. Thus, the reacting alkene bond in the transition state is shown in the images below to be a full 'bonded' interaction through an oxygen atom to the metal (there is a 'stick' depicted joining the atoms together). For the (R,R) transition state:
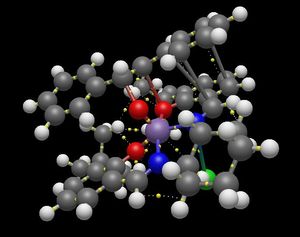

For the (S,S) transition state:
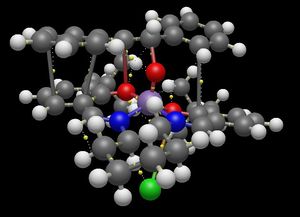


(The last image shows more clearly the results of the QTAIM calculation obscured by the 'sticks' on previous images.) Following the relatively strong interactions from the central reacting alkene through the ligand's oxygen atom to the fused six-membered ring of the ligand, it can be seen that in the (R,R) transition state, the interaction can be traced to the ring-junction proton that is pointing up towards the reacting stilbene (shown in the image below).

In the (S,S) transition state the strong interaction with the alkene and the metal's chelating oxygen atoms is closest to the fused ring junction proton that is pointing down away from the reacting stilbene.

The result is that the reacting stilbene in the (S,S) transition state goes with the 'natural twist' imparted on the plane of the metal's Schiff-base ligand by the fused ring, giving an accentuated distortion of it. The binding of the reacting stilbene to the complex goes against the (R,R) transition state's natural distortion, reversing it (compare the signs of the dihedral angle of the N-N-O-O plane), resulting in a more planar arrangement at the metal's chelating atoms. It is as if the catalyst is 'spring-loaded' like a mouse trap and the stilbene sets it off.
Testing the prediction
To test the prediction that the binding of stilbene in the (S,S) configuration, causing a greater distortion and weakening of the ligand field in the metal complex, freeing-up electron density that populates the anti-bonding orbitals, makes epoxidation slower in the (S,S) pathway kinetically favouring the formation of (R,R) stilbene oxide, the height of the potential energy barrier in the reaction can be investigated. A higher-energy transition state for the (S,S) pathway would indicate faster (R,R) stilbene oxide formation.
From the Gaussian log file of the (R,R) transition state:
Sum of electronic and thermal Free Energies= -3574.921174
From the log file of the (S,S) transition state:
Sum of electronic and thermal Free Energies= -3574.923087
These values represent the standard Gibbs free energies of the transition states.
Standard Gibbs free energy difference, ddG = G(R,R) - G(S,S) = -3574.921174 a.u. + 3574.923087 a.u. = 0.001913 a.u. = 1.20 kcal/mol = 5.02 kJ/mol.
The ratio of the two species, K, is related to the Standard Gibbs free energy difference, delta G, by the relationship
delta G = RTlnK
which rearranges to
K = exp[(delta G)/RT]
so
K = exp[(5022.5 J/mol)/(8.314462 J/K/mol x 298.150 K)] = exp[2.026] = 7.58
suggests that the thermodynamic ratio of the transition states is around seven- or eight-fold in favour of the lowest-energy transition state... which is the (S,S) transition state. It appears that the prediction involving the antibonding electron density feeding into the forming bond is not correct. A revised understanding would be that transition state with the greatest distortion of the ligand from the planar arrangement (which would be favoured for interaction with the d-orbitals) leads to the highest-energy transition state, least favouring the formation that transition state.
After Schneebeli, Hall, Breslow and Friesner (2009)[6], who studied a range of catalytic systems and agreed that enantioselectivity can be modelled successfully, the enantiomeric excess, ee, is given by
ee = (exp[ddG/RT]-1)/(exp[ddG/RT]+1) = (K-1)/(K+1)
so
ee = 0.7670 = 76.70%
Enantiomeric excesses for other catalysts and epoxides
A look at some other transition states and the results of energetic analyses are summarised below.
Shi oxidation of stilbene
The computed transition states available for the epoxidation of stilbene with the Shi catalyst included one high-energy (R,R) transition state which was excluded (not representative of the majority of transition states in the population of transition states) leaving two (R,R) transition states to be averaged (mean value -1534.687530 a.u.); the available (S,S) transition states included one particularly high-energy transition state with the stilbene 'lodged' on the two alkyl chains that should have guided it towards the reactive centre, two (S,S) transition states of low energy being averaged (mean value -1534.692838 a.u.) with the assumption that both could be reasonably representative of the transition states in the population. The difference in standard Gibbs free energy was then 3.33 kcal/mol. The value of K was found to be 276.38 with an enantiomeric excess, ee = 99.28%, favouring (S,S) stilbene oxide over (R,R) stilbene oxide. A more optically pure epoxide product should therefore be expected with the Shi catalyst than with the Jacobsen catalyst. (Considering only the lowest-energy conformations would have boosted the calculated enantiomeric excess to 99.66%.)
Jacobsen oxidation of cis-beta-methylstyrene
Interestingly, in lowest-energy pathways for the oxidation of cis-beta-methylstyrene, the approach of cis-beta-methylstyrene with the alkene bond nearer to the chelating nitrogen atom of the Schiff-base ligand was lower in energy in both transition states than an approach in which the alkene bond being oxidised (with the preservation of the aromaticity of the phenolic ring) was nearest to the oxygen ring. In the oxidation of stilbene, only a strong interaction with the oxygen atom of the Schiff base ligand was seen (the nitrogen was not involved). Here, this conformations were discarded form the calculations, in favour of the lower-energy interactions with the nitrogen atoms. For the nitrogen approach only, the difference in standard Gibbs free energy between (R,S) and (S,R) transition states was 5.33 kcal/mol. K was found to be 276.38 and the enantiomeric excess, ee = 99.98% in favour of (R,S) cis-beta-methylstyrene oxide. (Comparing only the transition states with the alkene approaching over the ring oxygens would have given an enantiomeric excess of 93.28% in favour of (R,S) cis-beta-methylstyrene nonetheless, perhaps confirming that the Jacobsen catalyst is 'spring-loaded' ready to oxidise only one enantiomer of the alkene.)
Jacobsen oxidation of trans-beta-methylstyrene
As with the cis-isomer above, the epoxidation of trans-beta-methylstyrene with the Jacobsen catalyst can proceed with the alkene approaching over the nitrogen or over the oxygen of the Shiff-base coordinating ring. As was the case with the cis-isomer, the approach over nitrogen gives the lowest energy transition states. The formation of (S,S) trans-beta-methylstyrene is favoured with an enantiomeric excess of 99.98% - this is considering only the lowest energy nitrogen approach. (Considering only the oxygen approach would have given an enantiomeric excess of 95.22%.)
Shi epoxidation of trans-beta-methylstyrene
An enantiomeric excess of 99.94% in favour of (R,R) trans-beta-methylstyrene is found when considering the lowest-energy (R,R) and lowest-energy (S,S) transition state of those available. This is a different enantiomer of trans-beta-methylstyrene from that given by the Jacobsen catalyst.
Calculated optical rotations
Calculating the optical rotation using the CAM-B3LYP/6-311++g(2df,p) basis set with structures optimised independently at the B3LYP/6-31G* level (and checked confirming an absence of imaginary frequencies) gives this as +232.62 degrees for (R,R) stilbene oxide and -232.08 degrees for (S,S) stilbene oxide. While the rotations are almost opposite but equal in magnitude, the calculations have an inherent variability.
Calculating the optical rotation of trans-beta-methylstyrene using the CAM-B3LYP/6-311++g(2df,p) basis set with structures optimised at the B3LYP/6-31G* level of theory gave a values of +21.05 degrees and +21.92 degrees in repeated calculations on the (R,S) enantiomer, showing the inherent variability of the calculation itself. Optimising the structure again at the CAM-B3LYP/6-311++g(2df,p) level and repeating the optical rotation calculations with the CAM-B3LYP/6-311++g(2df,p) basis set gave larger optical rotations of +31.34 degrees and -31.44 degrees for the (R,S) and (S,R) enantiomers respectively. Again, a small variation but overall reproducibility within one degree. Assuming the CAM-B3LYP/6-311++g(2df,p) model chemistry to give better optical rotation values, the calculated values for stilbene above should be considered an underestimate (roughly two-thirds the true value).
Conclusions
Model chemistry is very useful: it lets the chemistry student see the bigger picture of reactivity!
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283; DOI:10.1021/ja00157a043
- ↑ M. Karplus, J. Am. Chem. Soc., 1963, 85, 2870–2871; DOI:10.1021/ja00901a059
- ↑ E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen, W. Yang, J. Am. Chem. Soc., 2010, 132, 6498-6506; DOI:10.1021/ja100936w
- ↑ S. Yamada, Coord. Chem. Rev., 1999, 190-192, 537-555.
- ↑ S. J. Gabrowski, J. Mol. Model., 2013 19, 4713-4721.; DOI:10.1007/s00894-012-1463-7
- ↑ S. T. Schneebeli, M. L. Hall, R. Breslow, R. Friesner, J Am Chem Soc., 2009, 131, 3965-3973; DOI:10.1021/ja806951r
