Mod1db2409wd6

Year 3 Computational Lab

Module 1: The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

---

The Hydrogenation of Cyclopentadiene Dimer

Introduction

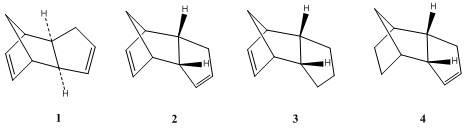
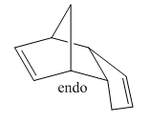
The Diels Alder reaction is a widely used reaction for C-C bond formation. However, the reaction can produce two products, the exo and the endo adducts. It has been thoroughly documented that despite the exo product being the more thermodynamically stable product the endo product dominates due to kinetic effects. Therefore, when it comes to kinetically controlled Diels Alder type reactions, like the dimerization of cyclopentadiene or the reaction of Cyclopentadiene and maleic anhydride the endo product dominates. The ability of reagents to donate non-bonding electron density via favorable secondary orbital interactions allows the endo product to proceed via a different reaction coordinate with the formation of a lower energy transition state, affording a faster rate of reaction. Therefore, MM2 calculations will be used to highlight the stability of the two products and support the endo product as being the kinetic product. Additionally, the table below defines the breakdown for the MM2 calculation.

Table 1 Defined parameters

Parameter	Definition
Stretch	The sum of all diatomic bond stretches
Bend	The sum of all triatomic bond angle deformations
Stretch bend	A correction to account for the coupling between stretching and bending
Torsion	The sum of all tetra-atomic bond torsions, modeled by a cosine dependence upon angle
Van Der Waals	The sum of all Van der Waals repulsions using a Lennard-Jones potential
Dipole-Dipole	The sum of all electrostatic attractions of individual bond dipole

Table 2 MM2 Result of All the 4 Structures

Structure	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 Van de Waal's	1,4 Van de Waal's	Dipole/Dipole	Total Energy
1	1.2855	20.5792	-0.8382	7.6571	-1.4171	4.2324	0.3776	31.8766 kcal/mol
2	1.2512	20.8495	-0.8354	9.5102	-1.5420	4.3167	0.4474	33.9976 kcal/mol
3	1.2360	18.9435	-0.7612	12.1212	-1.5037	5.7278	0.1631	35.9267 kcal/mol
4	1.0969	14.5223	-0.5490	12.4984	-1.0679	4.5107	0.1407	31.1521 kcal/mol

Exo Vs Endo

The structures for the endo and exo products were modeled on ChemBio 3D Ultra and the energy of each structure was minimized using MM2 calculations. The MM2 operation calculates various parameters i.e. the stretching energy which describes the positions of atoms related to their equilibrium positions. Thus, each positive parameter contributes to the instability of the structure. In the above table it is clear that the exo product is more stable than the endo product by 2.121 Kcal/mol. Therefore, if the endo is less stable but dominates as the major product, it must be formed via a kinetic pathway with a lower barrier of activation. This barrier has been investigated experimentally as being 33.0 Kcal/mol 4.4 Kcal/mol less than the exo product which supports the kinetic pathway . Furthermore, the torsion is a distinguishing parameter between the two isomers as the endo product exhibits a larger value due to bending of its structure back on itself. However, electronic contributions counter this parameter due to favorable orbital interactions. Perhaps by using the MOPAC/PM6 function the endo product would be identified as the most stable product. A slightly larger van der Waals value is likely due to distances between Carbon atoms lying closer to the maximum attractive distance .

Hydrogenation of Endo Isomer

The energies of the mono-hydrogenated isomers suggest a large energetic favoring of Structure 4 of 4.7746 kcal/mol. Thus, under thermodynamic control molecule 4 will be formed, but under other conditions calculations about the transition state and mechanism would be required. This large energetic difference can be mostly attributed to the relative bending energies of the two isomers. Structure 4 has a bending energy which is 4.4212 kcal lower than structure 3, a significant destabilizing contribution for structure 3. The internal bond angles for the alkene in each hydrogenated isomer can be calculated. Thus, for structure 3 and 4 the C=C-C angle was found to be 108o and 113o respectively. This deviation from the ideal sp2 angle of 120^o suggests that both structures experience ring strain with structure 4 being closer to the ideal geometry, supporting its implied thermodynamic stability. Furthermore, the difference in energy between the two hydrogenated isomers can be mostly attributed to the bending term that takes into account bond angle deviations from the ideal hybridized value. The specifics regarding the kinetic product cannot be discovered using MM2 calculations. Either product could be the kinetic product as the rate of hydrogenation can be affected by the release of ring strain or inhibited by steric crowding. Thus, further evidence would be required in order to confidently assign the kinetic product.

---

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

For the synthesis of taxol, the observed intermediate exists with a carbonyl group with differing stereo chemistry (carbonyl pointing up or down). Atropisomerism is often found in cases with restricted rotation of aromatic rings. However, in this case atropisomerism occurs due to the high barrier to rotation for the carbonyl to flip its orientation, inhibiting rotation about the single bond. The high steric strain barrier to rotation is sufficient to allow the isolation of single conformers . For the Taxol synthesis the compound isomerises through asynchronous bond rotation to its most stable form on standing but not in situ . Therefore, by using MM2 Force Field calculations the most stable isomer can be calculated and a stereospecific synthesis can be used to produce an enantiomerically pure product. This stereo chemical control is of the utmost importance as the major application of taxol is for medicinal purposes (anti-cancer drug). Thus, significant enantiomeric purity must be achieved first before it can become approved and available to the public. In addition, a slow hydrogenation of the alkene moiety is observed, which is due to the effect of "Hyperstable Alkenes" which will explored later.

The table below displays MM2 breakdown for the two isomers calculated on Chembio3D ULtra. In addition, the MMFF94 minimization energy was also calculated for comparison. Furthermore, when minimizing the energies of molecule it is important to ensure that the molecule is at its true minimum, not a local minima on Potential Energy Surface caused by small distortions of the molecule. Therefore, many different starting points ensure the true minimum is obtained.

Table 3 Relative Minimised Energies Of Molecules 9 and 10 calculated with MM2 force field

Value	Molecule 9 (MM2)	Molecule 10 (MM2)
Stretch	3.0021 kcal/mol	2.5609 kcal/mol
Bend	17.005 kcal/mol	13.2020 kcal/mol
Stretch-Bend	0.1895 kcal/mol	0.2653 kcal/mol
Torsion	19.141 kcal/mol	20.3037 kcal/mol
Non 1,4 VDW	-0.2502 kcal/mol	-1.9845 kcal/mol
1,4 VDW	13.7521 kcal/mol	13.9531 kcal/mol
Dipole/Dipole	-1.6985 kcal/mol	-1.6022 kcal/mol
Total Energy	54.9699 kcal/mol	46.6984 kcal/mol

Table 4 Relative Minimised Energies Of
Molecules 9 and 10 calculated with MMFF94 force field

Value	Molecule 9 (MMFF94)	Molecule 10 (MMFF94)
Total Energy	82.8065 kcal/mol	65.2918 kcal/mol

As shown above, both the MM2 and MMFF94 calculations show molecule 10 as being the most stable geometry for the intermediate. The energy difference of MM2 calculation is 8.2715 Kcal/mol, a sufficient energy difference to form molecule 10 as the major thermodynamic product assuming the reaction progresses under thermodynamic control. The MM2 and MMFF94 calculations appear to differ slightly, which is quite obvious as calculations with different force fields cannot be compared. In molecule 10 the carbonyl group is sufficiently far away from the methyl groups to alleviate steric clashing. However, for molecule 9 quite the opposite is true and the close proximity of the groups, results in instability through unfavorable ring strain and steric clashes. The most contributing parameter is clearly the bending value of around 17.005kcal/mol for molecule 9, which is alleviated to 13.2020 kcal/mol for molecule 10. Furthermore, the reliability of this data could be improved by identifying some higher energy conformations by modifying some key structural features.

Hyperstable Alkenes

The reason why molecules 9 and 10 are less reactive is because they are referred to as 'hyperstable alkenes'. This term describes the situation where the alkene is less strained than the hydrogenated alkane, where the olefin strain energy is negative. The OSE is defined as the difference between the strain energy of the olefin and the corresponding saturated alkane. This property adds to the stability of the molecule as hydrogenation is disfavored slightly by the increase in strain. Thus, the OSE value can be calculated by using MM2 calculations to minimize the energy of the hydrogenated products. The table below shows differing energy values between the hydrogenated and non-hydrogenated intermediates.

Table 5 Above the Ring

Parameter	Intermediate Click Here	Hydrogenated Intermediate Click Here
Bend	17.0050	22.2725
Stretch-Bend	0.1895	1.0753
Torsion	19.141	22.2471
Non-1,4 VDW	-0.2502	1.1661
1,4 VDW	13.7521	18.4006
Dipole/Dipole	-1.6985	-1.7395
Total Energy (kJmol-1)	54.9699	68.0995

Table 6 Below Ring

Parameter	Intermediate Click Here	Hydrogenated Intermediate Click Here
Bend	13.2020	14.5395
Stretch-Bend	0.2653	0.5707
Torsion	20.3037	21.3264
Non-1,4 VDW	-1.9845	-0.6574
1,4 VDW	13.9531	14.8063
Dipole/Dipole	-1.6022	-1.7385
Total Energy (kJmol-1)	46.6984	51.9191

The OS calculations below suggest that molecule 9 is the most hyper stable alkene due to larger torsion value for the hydrogenated intermediate, requiring more energy to overcome the destabilizing effect. Furthermore, Bredt's rule states that a double bond cannot be placed at the bridgehead of a bridged ring system, unless the rings are large enough. The result of having a double bond on a bridgehead is to form a Tran’s double bond on a ring, which is not possible for small rings due to significant ring and torsional strain . However, in this case the alkene is located on the 8-membered ring which is more versatile, orientating itself sufficiently to allow stabilization of the double bond with an angle closer to 120^o. This theory can be extended to help explain the outcome of electrophilic attack at the electron rich alkene. Due to sterics, the electrophile would have to attack the less hindered end of the alkene, resulting in the formation of a tertiary carbocation. The positive charge of the cat ion occupies an empty p orbital, forcing the centre to drop to a sp2 hybridised center. Thus, two geometries start to compete with one another, the trigonal planer geometry of the sp2 carbons and the bridge trying to force the geometry towards an unstable tetrahedral structure. Thus, the electrophilic attack on the alkene is an unfavorable process, thus inhibiting the rate of hydrogenation.

OS above = Torsion (alkene) 19.141 - Torsion (alkane) 22.2471 = -3.1061 kcal/mol

OS below = Torsion (alkene) 20.3037 - Torsion (alkane) 21.3264 = -1.0227 kcal/mol

---

Regioselective Addition of Dichlorocarbene

Creating a report page

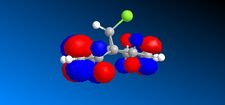
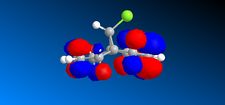
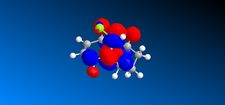
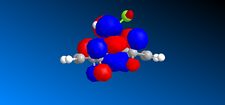
In the previous sections the electronic contributions such as secondary orbital interactions for the Diels Alder reaction were ignored and a purely mechanical model was used to account for molecular stabilities, but was unable to predict the endo product as the major product. Thus, the semi-empirical molecular theory approach, accounts for electronic contributions to reactivity. Therefore, this method should model the electron distribution of the molecule and as a result provide a wealth of information regarding spectroscopic properties and bond lengths. In order to model the electronic parameters of molecule 12 the geometry was firstly optimised using MM2 calculations. The MOPAC/PM6 method was then used to create an approximate model of the valence electron molecular wave function.In this section the attack of an electrophile on a specific asymmetric molecule with two alkene moieties will be investigated. Therefore, the molecular orbitals of the molecule will be calculated and used to predict the site of electrophilic attack.

Table 7 PM6 Molecular Orbitals of diene and monoene

Molecular Orbital	Dialkene	Monoalkene
HOMO-1
HOMO
LUMO
LUMO+1
LUMO+2

The MO's shown on the left were calculated using MOPAC/PM6 and are not what we would expect to see for this molecule . It is likely that the observed result arose from a calculational error in the shapes and sizes of the molecular orbitals. This observation clearly suggests a limitation or inaccuracy in the MOPAC/PM6 method. In order to confirm this observation the Molecular orbitals will be calculated using the AM1 function and compared in order to elucidate where the inaccuracy lies. The MO's are displayed in the table below and identifies the correct molecular orbitals. Therefore, the inaccuracy can be definitively associated with the PM6 calculations.

Table 7* AM1 Molecular Orbitals of diene and monoene

Molecular Orbital	Dialkene	Monoalkene
HOMO-1
HOMO
LUMO
LUMO+1
LUMO+2

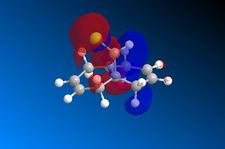For the HOMO, the majority of its electron density is centered over the endo double bond. This results in an afforded nucleophilicity of the endo double bond over the exo double bond, making it more susceptible to electrophilic attack. Furthermore, The LUMO's electron density is centred on the exo double bond over a п* antibonding orbital. This suggests that the endo double bond is susceptible to nucleophilic attack. In addition, for the HOMO-1 we can see a secondary orbital overlap between the electron density of the double bond and that on the chlorine. Thus, due to chlorine's electronegative character, we would expect electron density from the alkene π cloud to be drawn away by the chlorine. This loss of electron density would result in a reduced affinity towards electrophilic attack. However, in the LUMO+2 we can essentially see the antibonding orbital for C-Cl bond. As it can only direct itself towards the exo double bond, electron density from the exo double bond will be donated into the C-Cl σ* orbital via a pi-sigma* interaction (endo double bond not involved in this interaction, preserving its electron density). Therefore, when the exo double bond is removed we would expect a strengthening of the C-Cl bond as its IR vibration would shift to lower wave numbers as the donation into its anti bonding orbital is removed. Furthermore, the MO calculations support the rationalization of the molecules reactivity and should be further supported by the IR calculations.

Table 8 IR Spectra of 12 and its Monohydrogenated Derivative

Alkene	C=C exo stretch	C=C endo stretch	=C-H exo stretch	=C-H endo stretch	C-Cl stretch
Diene (click to view spectrum)	1738cm-1(C=C stretch)	1758cm-1(C=C stretch)	3010cm-1(=C-H stretch)	3024(=C-H stretch)	690cm-1(C-Cl stretch)
Monoene (click to view spectrum)	-	1754cm-1(C=C stretch)	-	3030cm-1(=C-H stretch)	682cm-1(C-Cl stretch)

The IR spectra shown above where computed via MM2 and MOPAC/PM6 minimization followed by B3LYP/6-31G (d,p) Gaussian geometry optimization and frequency calculation. Furthermore, the effects of electron withdrawing and electron donating groups will be discussed later. The table above clearly shows the IR vibrational frequencies with the monene containing only one endo C=C and =C-H stretch. In addition, the absence of the exo double bond should result in a lower C-Cl energy stretch as the bond is weakened by the π-σ* interaction from the exo double bond. This is in fact clearly shown as the monene displays a C-Cl stretch at 682cm^-1 8cm^-1 less than the diene. As a result of this orbital interaction the exo double bond becomes higher in energy, weakening its double bond character.

Further Studies with SiH3 and CN

Table 9 Further Studies with SiH3 and CN

Substituent	C=C exo stretch	C=C endo stretch	=C-H symmetric exo stretch	=C-H symmetric endo stretch	C-Cl stretch
SiH 3 (click to view spectrum)	1737.07cm-1(C=C stretch)	1708.61cm-1(C=C stretch)	3179.64 cm-1(=C-H stretch)	3149.47(=C-H stretch)	773.42cm-1(C-Cl stretch)
CN (click to view spectrum)	1737.76 cm-1	1724cm-1(C=C stretch)	3183.71cm-1	3187.47cm-1(=C-H stretch)	540.02cm-1(C-Cl stretch)

The endo alkene was substituted with ED and EW groups to discover its effect on the IR spectrum. The stretching region found around 2200-2240cm^-1 for SiH3 is due the stretching motion of the SiH3 group. The CN stretch was located at 2339.78cm^-1. There appears to be little difference between the SiH3 and CN C=C stretching energies suggesting that it is not involved in a orbital interaction. However, for SiH3 the exo C-H stretch is at a higher frequency, contrary to the observed CN effect. Furthermore, the C-Cl stretching frequencies appear to increase slightly for the silyl group suggesting a weakening of the bond through electron donation. For the electron withdrawing group CN, the stretching frequency decreases thus, strengthening the C-Cl bond slightly by reducing the effect of the π-σ* donation.

---

Monosaccharide chemistry: glycosidation

As depicted in the image below the site of attack for the nucleophile is governed by the orientation of acetyl group. As the leaving group is lost via electron donation from the oxygen, the neighboring group is able to stabilize the oxonium cation through electron donation and stericaly block one side of attack allowing exclusive attack from the opposite end. In this section of the report computational techniques will be used to elucidate the effect of neighboring group participation for a glycosidation reaction. The energies and instabilities of the oxonium ion intermediates will be calculated, in order to depict the most stable intermediate.

align="right"

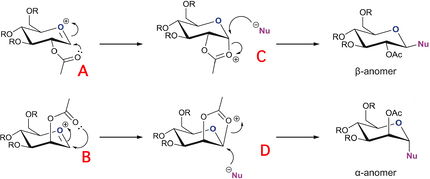
Furthermore, the four conformors A,B,C and D and their corresponding ring flipped counterparts were all drawn on ChemBio 3D and were subjected to MM2 and MOPAC/PM6 ministrations. The MM2 minimization served as a crude geometry optimization, The MOPAC/PM6 minimization was then used for further energy minimization taking into account orbital interactions within the molecule. The difference between these two methods is more apparent for larger systems due larger intramolecular interactions. However, before these calculation a sufficiently small R group had to be selected that would not electronicaly or mechanically interfere with the rest of the molecule, creating local minima. Thus, a small mechanically and electronically labile Me group was the logical option, as the introduction of more complex heteratoms would affect the electron distribution within the molecule, affecting the MOPAC/PM6 minimization. The table below shows the enthalpy of formation for the 4 conformational pairs.

Table 10 Saccharide energies

-	AClick Here	A'Click Here	B Click Here	B'Click Here	C Click Here	C'Click here	D Click Here	D' Click Here
MM2 minimisation kcal/mol	17.5621	21.1133	35.3975	36.3671	48.6000	60.3556	48.8210	111.1179
Heat of Formation kcal/mol	-91.9698	-83.71028	-88.51336	-85.4233	-260.1587	-240.7784	-260.10187	-245.74435

As shown above the corresponding heat of formation and total energy values for the 8 saccharides are shown above. The MM2 Force Field calculation strongly suggest that for the equatorial conformer (A/A*) attack from below the plane of the ring (A) is thermodynamical more stable. This was further supported by the fact that when optimizing the geometries of dashed saccharides they often reverted back to more stable conformation. The same can seen for monosaccharide B suggesting that a conformation in which the acetyl group is orientated so that there is a favorable orbital overlap with the oxygen within the ring is the most stable. The afforded stability of B is slightly less than A (3.5512kcal/mol) with a value of 0.9696kcal/mol. This may suggest that the optimized structure for B or B' is located on a local minima perturbing the true gain in stability. In addition, the values also suggest that A is more stable than B which is likely due to the extra steric instability afforded by B due to stronger axial repulsions between substituents.

Furthermore, we can continue to analyze the intermediates of the reaction and decipher their inherent stability. For intermediate C and D the optimisation calculations suggest a higher stability for the cis conformation of the acetyl (C/D) over its trans conformation (C'/D'). In addition, the MM2 geometry optimization calculations do accurately reflect the most stable intermediate. Due to the anomeric effect and reduced steric clashes from axial crowding, C would be expected to be the most stable intermediate (48.600kcal/mol). The axial attack from below the ring of a nucleophile on structure D should result in the formation of the most stable α anomer product due to anomeric effect. Computational techniques could be used to ascertain the major product and confirm the above assertation. Nonetheless, it would appear that the Operations have provided values that fit the rationalization of the glycosidation reaction. The bond lengths and bond angles for both intermediates can be seen in the table below.

Table 11 carbonyl/oxonium bond distances

-	A	A'	B	B'	C	C'	D	D'
bond distancee Ā	2.4	1.6	1.6	1.6	1.4	1.4	1.4	1.4
bond angle (o)	106	113	105	106	104	103	102	103

The analysis can extended further by analyzing the bond lengths and angles for the 4 monosaccharrides. The data below represents an important observation. Disregarding the value for A as an anomalous value, the measured distances are smaller than the sum of the Van Der Waals radius for oxygen and carbon (3.32A). This observation may be due to fact that the MOPAC/PM6 geometry optimization ignores rigid bonds. Thus, the calculation may have created its own favorable bonding interactions. In addition, the bond angles between the oxonium ion and the oxygen on the carbonyl are found in the region of 102-113^o. These values are extremely close to the Burgi Dunitz angle of 107^o , this is the angle were maximium orbital overlap between the lone pair on oxygen and the π* system on carbon is achieved. Finally, the bond distances for the intermediates are identical for each monosaccharride C/C' and D/D'.

---

Mini Project

Introduction

The idea of Click chemistry describes the chemistry tailored to generate substances quickly, stereo-specificly and reliably through the joining of small molecular units. The topic of this mini product will revolve around the azide alkyne [3+2] cyclo-addition. The clycloaddition reaction between a azide and an alkyne results in the formation of two C-N bonds. The reaction preserves the alkene configuration as regioslectivity is controlled by the by frontier orbital interactions, and substrates with electronically distinct substituents tend to react with high regioselectivity. However, the reaction forms two regiomeric product A and B. Under Cu(1) catalysis, the 1,4 isomer A dominates. Whereas under Ru(II) catalyzed reactions the 1,5 isomer B is formed as the major product. However, various tailored Ru catalysts have been able to selectively form the 1,4 adduct as wel .

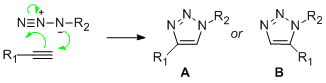
For the purpose of this mini project the R groups that will be used are one Ph group and one methy Ph group. The Azide-Alkyne Huisgen Cycloaddition is a 1,3 dipolar cycloaddition to give 1,2,3-triazole. The reaction affords a mixture of the 1,4- adduct and the 1,5-adduct at 98°C in 18 hours . However, the copper catalyzed reaction exclusively yields the 1,4 disubstituted 1,2,3-triazole. The reaction is often run with numerous Copper(I) salts, such as CuI and CuOTf.C6H6, but generally must be run with a acetonitrile as a co solvent and a nitrogen base. Additionally, unwanted diacetylene and bis triazole are sometimes formed as unwanted by-products. The reactions initial step involves in situ reduction of Copper(II) salts with sodium ascorbate in aqueous alcoholic solvents affording the 1,4-triazole at room temperature in high yield with a small catalyst loading of 2mol % . The reaction has broad application and is compatible with a range of functional groups and can utilizes primary, secondary, tertiary substituted and aromatic azides. The reaction is thought to proceed via a stepwise manner, begging with the generation of Copper(I) acetylide. previous studies have elucidated the mechanism and have identified a preference for the stepwise addition (5-8) by approximately 12 to 15kcal/mol leading to a six-membered metallocycle[6]. The proposed intermediates for a Ru catalyzed reaction are also shown to the right .

Tabe 12 Ru Vs Cu catalysis

Cu catalysis	Ru catalysis
	‎

The specific reaction that will be studied for this part of the report is shown above. The MM2 minimization values for the 1,4 and 1,5 adduct displayed in the table below. The Crude MM2 calculation provide some approximate information regarding the most stable geometric adduct. The calculations clearly how that the 1,4 adduct is more stable by only 6.5698kcal/mol. This afforded stability can seen in the breakdown of the calculations parameters. The greatest difference is found in the bending parameter. The 1,5 adduct has a larger Bend value . This analysis will be extended to include electronic effects by using the MOPAC/PM6 method.

Table 13 MM2 Result for 1,4 and 1,5 adducts

Structure	Stretch	Bend	Stretch-Bend	Torsion	Non-1,4 Van de Waal's	1,4 Van de Waal's	Dipole/Dipole	Total Energy
1,4 Click Here	0.7747	13.1061	-0.0300	-14.8387	-1.6746	14.7210	-1.4057	10.6530 kcal/mol
1,5 Click Here	1.1062	18.2961	0.1075	-15.7232	0.7270	14.3720	-1.6628	17.2228 kcal/mol

The MOPAC/PM6 calculations shown below result in significant bending/twisting of the planes of the aromatic rings for both adducts. The values for the heat of formation suggest that the 1,5 adduct is in fact the most stable, contrary to the MM2 values. This, may suggest an extra afforded electronic stability from the bending of the aromatic rings. However, the AM1 calculations do agree with the MM2 values. The AM1 geometry has been omitted from the table below due to large similarity between the AM1 and PM6 geometries.

Table 14 MOPAC PM6 and AM1 Result for 1,4 and 1,5 adducts

Structure	Heat of formation (PM6) (kcal/mol)	heat of formation (AM1) (kcal/mol)
1,4 Click Here for PM6 geometry	107.76398	142.13006
1,5 Click Here for PM6 geometry	107.24772	143.44819

Qualitative anysis of MO's '

The Molecular orbitals for the two adducts are extremely similar and are found in the same locations with similar sizes and nodes. The HOMO for both adducts is located on the triazole. The LUMO for the both adducts if located on the aromatic ring closest the three Nitrogen's in the triazole. This qualitative analysis provides little information regarding the formation of the product as no obvious intramolecular electronic interactions can be seen. Perhaps an electronic analysis of the reactant would help elucidate the reaction mechanism and explain the strong regioslective effect of catalysis.

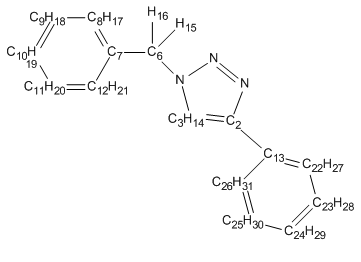
Spectroscopic Analysis:

Table 15 Assignment of 1,4 and 1,5 adducts

1,4 adduct	1,5 adduct

Table 16 CNMR spectra for 1,4 (Click Here)

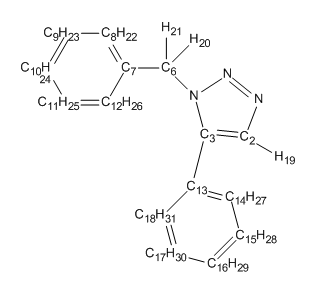
Carbon Assignment	Shift Lit(ppm)	Shift (ppm)	Difference (ppm)
2	148.0	144.85	3.15
3	120.1	116.983	3.117
6	41.0	54.87	-13.87
7	135.0	133.21	1.79
8 12,	128.1	124.522, 124.225 (124.3735)	3.7265
9, 11	128.2	124.814, 125.554 (125.184)	3.016
11	129.1	125.554	3.546
13	130.7	127.719	2.981
22, 26	125.7	121.316, 121.88 (121.598)	4.102
23, 25	128.9	124.969, 125.212 (125.0905)	3.8095
24	128.7	124.136	4.564
Average	-	-	1.812

Table 17 CNMR spectra for 1,5 (Click Here)

Carbon Assignment	Shift Lit (ppm)	Shift (ppm)	difference (ppm)
2	133.34	128.62	4.72
3	138.26	136.667	1.593
6	51.85	52.2454	-0.3954
7	135.66	134.101	1.559
8	126.93	123.404	3.826
9, 17	129.08	125.189, 125.068 (125.1285)	3.9515
10, 13	128.22	124.48, 124.696 (124.588)	3.632
11, 18, 15	133.26	125.488, 125.476, 125.613 (125.526)	7.734
12	127.22	123.672	3.548
14	133.26	126.23	7.03
16	129.64	125.876	3.764
Average	-	-	3.724

The calculated CNMR spectra for the 1,4 and 1,5 adduct deviate slightly from literature values and identify unique enviroments for every carbon resulting in additional Carbon chemical shifts. The inaccuracies observed may be caused by the conformational flexibility of the molecule. These inaccuracies could be minimised by adjusting the conformation of the adducts, ensuring that it is located on the bottom of it's PES and not a local minima. The Spectra for the 1,4 and 1,5 adduct are extremly similar and only very subtle differences are observed. For example the C3 chemical shift changes quite dramaticaly from 118 to 136ppm. After adjusting for the extra carbon enviroments the spectra appears to differ by approximately 1-4 ppm from that reported in literature, an acceptable difference. However, one or two anomolous shifts that deviated quite significantly, have decreased the average shift difference below its true value. Therefore, the shifts are likely to deviate by values slightly larger than 3ppm.

IR analysis

Table 18 IR Assignment of 1,4 and 1,5 adducts

Functional Group	1,5 frequency cm-1 (click here)	1,4 frequency cm-1 (click here)
N-N	1282.44	1309.39
C=C (Bnezyl)	1662.04	1663.49
C=C (Phenyl)	1662.51	1665.87
Benzyl CH2	3076.50, 3130.76	3071.13, 3122.66
C-H (Benzyl)	3193.76, 3203.78, 3210.68	3190.86, 3199.54,3209.52
C-H (Phenyl)	3201.25, 3209.12, 3214.49	3193.21, 3204.86, 3221.22
C-H (Triazole)	3275.91	3295.34
C-H Bend ( Benzyl)	743.46	744.04
C-H Bend (Phenyl)	779.65	771.53
C-H Bend (Triazole)	840.34	771.53

In the above IR analysis large similarities between the two structures can be observed. However, distinguishing parameters can be identified in the N-N stretch which shifts by 26.95cm_-1 and in the C-H triazole stretch which shifts 19.43 cm^-1. These distinguishing frequencies could be used as a secondary definitive spectroscopic method for the identification of the two adducts. These peaks alone are not enough to definitively assign them to the 1, 4 and 1, 5 triazoles.

Table 19 HNMR spectra for 1,4 (Click Here)

-	Shift Lit (ppm)	Shift (ppm)
1	5.58 (s,2H)	5.013(s, 1H), 5.9437(s, 1H)
2	7.66 (s, 1H)	7.5471 (s, 1H)
3	7.32-7.42(m, 8H)	7.4302(s, 1H), 7.632(t, 1H), 7.632(t, 1H), 7.6501(t, 1H), 7.7162(q,1H), 7.732(q,1H), 7.7458(q,1H), 7.7464(q,1H)
4	7.80(d, J= 7.2Hz, 2H)	8.0149(s, 1H), 8.8386 (s, 1H)

Table 20 HNMR spectra for 1,5 (Click Here)

-	Shift Lit (ppm)	Shift (ppm)
1	5.54(s,2H)	5.0181(s, 1H), 5.8915(s, 1H)
2	7.07(t, 2H, J=3.6Hz)	7.3839(s, 1H), 7.6588(m, 1H)
3	7.23-7.27(m, 5H)	7.697(m, 1H), 7.7047(m, 1H), 7.7177(m, 1H), 7.7499(m, 1H), 7.7941(m, 1H)
4	7.37-7.46(m, 3H)	7.8055(m, 1H), 7.8116(m, 1H), 7.9673(d, 1H)
5	7.773(s, 1H)	7.9802(d, 1H)

The HNMR calculations identify a unique enviroment for every H atom therefore the calculations had to be grouped in order to match them to the corresponding literature shifts. while the predicted Spectra does not match exactly it provides an approximate representation with approximate multiplicites. Both adducts conatined a singlet 2H peak in the region 5.55-5.58ppm. Both spectra identify a large multiplet or seperate multiplets between 7.23 and 7.46ppm. The 1,4 adduct identifies a large 8H multiplet, whereas the literature for 1,5 adduct identifies two seperate multiplets in this small region , a major discrepency. The discrepancy arises from the calculated spectra, for the 1,4 adduct two seperate multiplets are calculated, whereas for the 1,5 adduct a large 8H multiplet is calculated. When we move to ppm values around 7.8 we find a minor difference between the 1,4 and 1,5 adducts. For the 1,4 adduct a doublet is found at 7.8 ppm whereas for the 1,5 adduct we observe a singlet at 7.773ppm. However, the calculated spectra identifies a doublet for the 1,5 and a singlet for the 1,4 adduct. Thus, supporting a possible spectrascopic mismatch. Two possible explanations for this mismatch can be due to a calculational error or a literature error. A calculational error could have resulted from the similarity of the two adducts resulting in an emalgimation of the HNMR spectra. However, the fact that the CNMR appears to agree with literature, supports a calculational error.

Conclusion:

Throughout this report the accuracy of various computational techniques have been used and analysed in order to gain the most accurate data regarding the stabilities and Molecular orbitals of a molecule. Various computational limitations have arisen, such as the inaccurate PM6 MO's for the dichlorocarbene and some molecular conformations may not be located on the true minimum of their potential energy surface. Overall, the calculated computational data has allowed the successful rationalisation of molecular stabilities and mechanisms. Furthermore, the mini project was successful in differentiating the two adducts spectroscopically. Despite the NMR mismatch, it is clear that each adduct has its own characteristic chemical shift and multiplicity which could be determined experimentally. Therefore, the two adducts could be identified and distinguished from one another successfully using C and H NMR methods. The use of IR spectroscopy failed to provide a definitive determination of the two adducts due to their structural and functional group similarities. However, a slight change in the N-N stretch does provide a slight differential. Therefore, the IR spectra could be used as a final conclusive spectroscopic method in assigning to two adducts. In addition, the relative stabilities of the two adducts were calculated, assigning the 1, 4 adduct as the most stable thermodynamic product. Nonetheless, it has been thoroughly documented that both the 1, 4 and 1, 5 adducts can be individually synthesised with high yields, depending on the catalyst. Thus, despite a difference in stability different catalytic cycles have been designed to exploit this difference, and afforded one of the adducts as the major product.