Mod1GL1990

Module 1 - George Lane

In this module the molecular modelling will be investigated in order to explain why certain reactions pathways are preferred. Factors such as steric effects, Van Der Walls repulsions, hydrogen bonding and bond angles are all taken into account in order to calculate the energies of different molecules. This is a useful tool when investigating the activity or reactivity of structure in order to explain its behaviour. The molecular models used are based on assumptions from molecules which have been investigated in great detail to understand their characteristics.

In this first part this investigation uses molecular mechanics to explain the behaviour present in four different reactions

1. Hydrogenation of cyclopentadiene dimer
2. Stereochemistry and reactivity of an intermediate in the synthesis of taxol.
3. Regioselective addition of dichlorocarbene
4. Glycosidation

Hydrogenation of Cyclopentadiene Dimer

Cyclopentadiene, C₅H₈, is a liquid at room temperature and is useful in organometallic as a ligand with changing hapticity. A problem when storing cyclopentadiene is that dimerises via a Diels-Alder reaction. A Diels-Alder reaction is a form of [4π_s+2π_s] cycloaddition, which is a sub category of the pericyclic reactions. The reaction forms of two σ bonds and involves the 4π electrons from the diene and 2π electrons from the one of the double bonds found on the other cyclopentadiene, hence the name. The transition state of the cycloaddition contains the movement of 6 electrons so is Hückel aromatic and therefore under kinetic control.

Figure 1: Simple Overall Synthesis of Cyclopentadiene

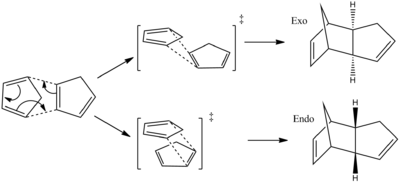
The two cyclopentadienes can approach each other in two different ways to form an endo or exo dimer. It is reported that the endo product is favored under kinetic control.

To investigated the observed outcome of the reaction the relative stabilities of the compounds was calculated using Molecular Modelling (MM2 force-field). The relative stabilities of the exo(1) and endo(2) dimer are calculated in addition the relative stabilities of the hydrogenated endo dimers (3) and (4). The bond strain, dihedral angles, torsion energies, bend energies and bond angles are all taken into consideration when calculating the molecules energy.

MM2 is popular molecular mechanics model, although assumptions are made the outcome is remarkably accurate. For example MM2 accounts for Van Der Walls forces, however it assumes that these forces are not effected by the environment the atom is in. The assumptions made are made as a result of experimental data.

Results and Discussion of Cyclopentadiene Optimization

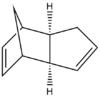
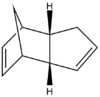
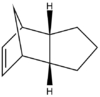
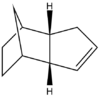
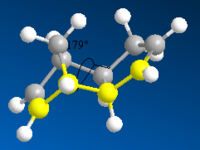
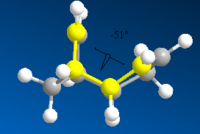
The table below shows the structures of the isomers [(1) + (2)] which can be formed as a result of the dimerisation of cyclopentadiene. The structures of (3) and (4) are the product of the hydrogenation on one of the double bonds present in the endo dimer. In structure (3) the double bond in the 5 membered ring is hydrogenated, whereas the double bond in the six membered ring is hydrogenated to form structure (4).

Exo cyclopentadiene dimer (1)	Endo cyclopentadiene dimer (2)	Endo cyclopentadiene dimer (3)	Endo cyclopentadiene dimer (4)
Cyclopentadiene dimer exo	Cyclopentadiene dimer endo	Cyclopentadiene dimer endo hydrogenated	Cyclopentadiene dimer endo hydrogenated
Cyclopentadiene dimer exo	Cyclopentadiene dimer endo	Cyclopentadiene dimer endo hydrogenated (3)	Cyclopentadiene dimer endo hydrogenated (4)
Dihedral angle : 179o	Dihedral angle : -51o	Dihedral angle : 108o	Dihedral angle : 113o

Figure 2: A table showing the structures and bond angles of the endo and exo dimers and the endo hydrogenation products

Compound	Stretch kcal mol-1	Bend kcal mol-1	Stretch-Bend kcal mol-1	Torsion kcal mol-1	1,4 VdW kcal mol-1	Dipole/Dipole kcal mol-1	Total Energy kcal mol-1
(1)	1.26	20.6	-0.838	7.65	4.23	0.378	31.9
(2)	1.25	20.8	-0.836	9.51	4.32	0.448	34.0
(3)	1.24	18.9	-0.761	12.1	5.73	0.163	35.9
(4)	1.10	14.5	-0.550	12.5	4.51	0.141	31.2

Figure 3: A table comparing the energies of the endo and exo dimers and the endo hydrogenation products

Endo and Exo Dimers

From the data it can be seen that the exo isomer is 2.1 kcal mol^-1 more stable than the exo. product. When comparing the energies which sum to form the total energy it can be seen that the torsion value is the value which is significantly different between the two isomers.

The larger the torsion energy the more strained the molecule is. The exo isomer has a smaller torsional energy (7.65 kcal mol^-1) and is therefore under less strain than the endo product which has a larger torsional energy (9.51 kcal mol^-1). The explanation of the differences can be seen by analysing the structures shown in figure 1. The torsional strain is caused by the 1,4 relationship between the highlighted carbons. This can also be shown by looking at the dihedral angles between the the four carbons. In compound (1) the highlighted carbons have a dihedral angle of 179^o which means they are in an antiperiplanar conformation, therefore the torsion energy is minimized. In compound (2) the dihedral bond angle is -50^o which between the higher energy gauche and eclipsed conformations.

From the data obtained from the computational investigation the endo product is not the favour product because it has the most stable product. Therefore the reaction can not be under thermodynamic control and must be controlled by the kinetics of the reaction. As a result we need to investigate the transition state of the reaction in order to understand the selectivity of the reaction.

Figure 4: The frontier orbitals of the exo(left) approach and endo(right) approach

By understanding the frontier orbitals of the cyclopentadiene the selectivity can be explained. Figure 4 shows the frontier orbitals of both cyclopentadiene molecules. The 'top' cyclopentadiene acts as the diene so therefore its HOMO is considered and the 'bottom' cyclopentadiene acts as the ene so its LUMO is considered. Where the orbitals overlap in phase with each other there is a favorable interaction. In the exo approach there are only two orbitals which are in the same phase and can overlap, whereas the endo approach has four orbitals which overlap in phase with each other. The orbital interactions which are involved in forming bonds are shown in green, and other interactions are shown in red.

From the frontier orbital diagram we can see that the endo structure has more favorable interactions when forming the transition state of the reaction. Therefore the transition state of the endo reaction is lower in energy than the transition state of the exo reaction. Via the computational analysis carried out it has been deduced that the reaction is under kinetic control and therefore will follow the endo reaction path which has the lowest energy transition state.

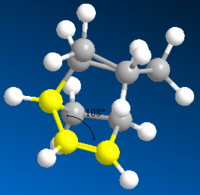
Hydrogenation of the Endo Cyclopentadiene Dimer

The endo dimer which has had the double bond in the six memebered ring hydrogenated (compound 4) has a lower energy by 4.7 kcal mol^-1. Again by comparing the individual energy contributions it can be seen that their is a large difference in the bending energies of the two compounds.

The bend component of the of the energies relates to the angular strain i.e. how much the bond angle is distorted from its preferred bond angle. The bond angles of compound 3 and 4 are 108^o and 113^o respectively. The ideal bond angle for an sp² hybridised carbon present in a double bond is 120^o so the closer the bond angle is to this ideal value the smaller the bend energy will be.

The bond angle of the sp² carbon in both compound 3 and 4 is not at the ideal 120^o because they are part of a ring which forces the bond angle to change. However the bond angle in compound 4 is closer to the ideal value because there the ring it is contained in does not have the bridge. The bridge acts to lock the ring in a configuration which causes the double bond to further away from the ideal angle.

To be able to deduce which product would be formed preferentially we need to know what type of control the reaction is under.

Experimentally it has been found that the reaction forms compound 4 preferentially. This information still doesn't allow us to work out if the reaction is under kinetic or thermodynamic control because compound 4 may have a more stable transition state as well as more stable product. The transition state would need to be modeled using molecular orbitals in order to determine if the reaction is under kinetic or thermodynamic control.

Sterochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Taxol is an important drug used to treat a variety of different cancers such as lung, ovarian and breast. During the synthesis of taxol there are two possible atropisomerism which can be used as intermediates.

Intermediate 9	Intermediate 10
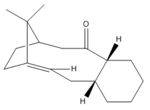Taxol intermediate carbonyl up, chair Taxol intermediate carbonyl up, chair	Taxol intermediate carbonyl down, chair Taxol intermediate carbonyl down, chair

Figure 5: Taxol intermediates 9 and 10.

An atropisomer is isomer which has been caused by the restriction of a double bond. Both the intermediates shown above are two stable minima on the molecules energy curve. The literature suggests that compound 9 is formed fastest however it converts to compound 10. This tells us that compound 9 is the kinetic product whereas compound 10 is more thermodynamically stable and therefore it must be the kinetic product. When compound 9 is formed it rearranges to give product 10 via a Oxy-Cope rearrangement.

In addition to the confirmation differences which could be caused as a result of directionality of the carbonyl group the conformation of the cyclohexane was adjusted to minimize the energy. The high energy twisted boat conformation is too high in energy to exist in as a product, therefore this conformation was ignored.

The energies of the both the chair and twist boat conformations of both compounds were analysised using MM2 and MMFF94 field process. It is clear that the energies of the chair conformations are smaller than the energies of the twist boat conformations when minimised with both MM2 and MMFF94. Also both minimisations suggest that compound 10 is the most stable. This supports the literature which says that compound 10 is the thermodynamic product.

Compound 10 is the major product because it contains σ-π* conjugation between the alpha carbons σ orbital and the carbonyls π* orbital. This overlap is largest when the carbonyl group is pointing 'down' and therefore the most stable conformation is observed.

The major difference in the energies of the two compounds is due to the different torsion energies.

Isomer	Minimised energy MMFF94	Minimised energy MM2	Stretch Kcal mol-1	Bend Kcal mol-1	Stretch-bend Kcal mol-1	Torsion Kcal mol-1	1,4-VDW Kcal mol-1	Dipole/dipole Kcal mol-1
Compound 9, Chair	56.9	44.9	2.2	12.1	0.3	21.0	13.0	-1.7
Compound 9, Twist Boat	76.3	53.3	2.9	17.2	0.5	21.3	14.5	-1.7
Compound 10, Chair	60.6	42.7	2.3	11.3	0.3	19.7	12.9	-2.0
Compound 10, Twist Boat	66.4	46.4	2.7	11.7	0.3	21.9	13.9	-2.0

Figure 6: The energies of the chair and twist boat conformations of compounds 9 and 10.

The alkene present in the compounds is hyperstable and as a result functionalisation of the alkene is abnormally slow. Hyperstability is a term used to describe the strain on the molecule with a double bond is less than the strain on the molecule if a double boond was present. The hyperstability of the alkene is due to the positioning of the bond at the bridgehead of the results which reduces the strain.

The hyperstability of the alkene means that the stability to the structure with the double bond and the π bond is greater than the energy which would be produced from the two additional C-H σ bond.

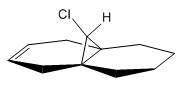
Regioselective Addition of Dichlorocarbene

The addition of dichlorocarbene to compound 12 is a [π+2π] cycloaddition. The shape and energies of the molecular orbitals can be calculated and used to explain any reactivity changes if the molecule is changed. The atomic orbitals can be displayed graphically and used to calculate the which double bond will be attacked by the dichlorocarbene

Figure 7: The reaction between dichlorocarbene and compound 12

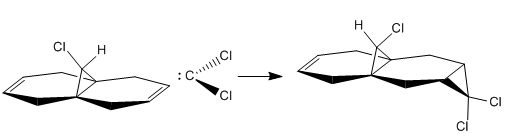
The reaction forms a mixture products depending which alkene bond is attack, the major product is the syn trichloride(72%) and the majority of the rest if the product is the disubstituted product(23%).

Molecular Orbitals

Figure 8: The unsymmetrical molecular orbitals produced by the MOPAC/PM6 method

Figure 9: The plane of symmetry which exists in compound compound 12

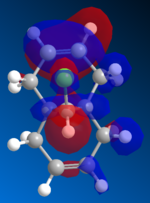
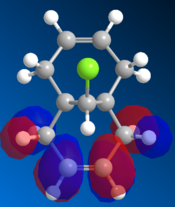
The orbitals are visually displayed in ChemBio3D using the MOPAC calculations to show the size and energies of the orbitals. The molecules energy is first minimised using MM2 then the molecular orbitals are calculated using the PM6 method. However the PM6 method produced molecular orbits which are not symmetrical. Therefor this method must have produced an error because compound 12 has C_s symmetry and therefor the orbitals should also show this symmetry. The orbital calculations are repeated with using the AM1 method in order to remove this mistake.

Stretch	Bend (kcal mol-1)	Stretch-Bend (kcal mol-1)	Torsion (kcal mol-1)	1,4 VDW (kcal mol-1)	Dipole/Dipole (kcal mol-1)	Total Energy (kcal mol-1)
0.620	4.73	0.04	7.67	5.80	0.112	17.9

Figure 9: The MM2 minimised energy for compound 12

HOMO -1	HOMO	LUMO	LUMO +1	LUMO +2
HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

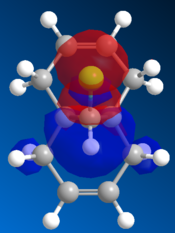Figure 10: The frontier orbitals calculated using MOPAC/AM1

Form the images it can be seen that there two double bonds behave differently. The double bond which is syn to the chlorine atom will be most reactive to electrophilies because it shows a large contribution to the molecules HOMO. The double bond which is anti to the chlorine atom will be more reactive towards a nuclearphile because it is the major contributor to the LUMO. The electron density of the LUMO is mainly formed by the π antibonding orbital of anti double bond. Since dichlorocarbene is a very strong electrophile it will be favorable for it to react at the syn double bond. Therefore the computational data and the experimental data are aligned.

Figure 11: MO diagram for the stabilisation of frontier orbitals

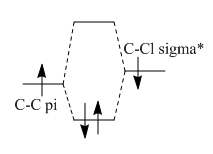
The double bond syn to the Chloride has an increased stability due to its orientation with relation to the C-Cl bond. The C-Cl σ* bond is able to donate electron density to the π orbital and cause it to be lower in energy. The C-Cl σ* orbital is low and similar in energy to the C=C π orbital due tot he electronegativity of the Cl atom. This allows the orbitals to overlap well and form a orbital which has a lower energy and therefore is more stable and therefore less nucleophilic so the carbene will attack the other double bond.

Vibrational energies

Figure 12: Compound 13

The vibrational stretching energies of both double bonds and C-Cl found within compound 12 were investigated using MOPAC/AM1. They are compared to the values obtained from structure 13.

Bond	Structure 12		Structure 13
	Wavenumber of stretch/cm-1	Vibration	Wavenumber of stretch /cm-1	Vibration
C-Cl	771		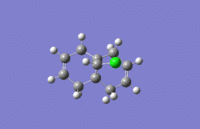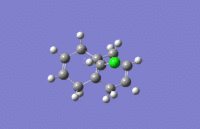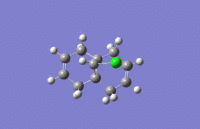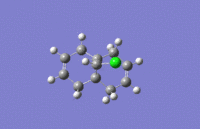775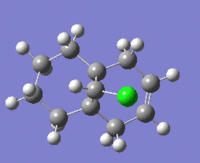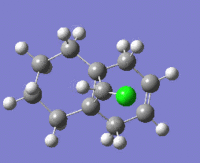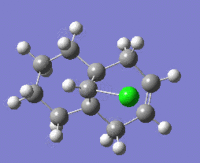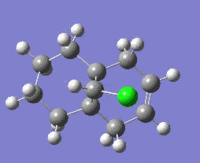
C=Csyn	1758		1757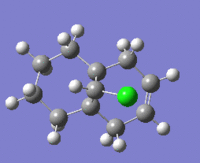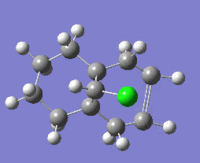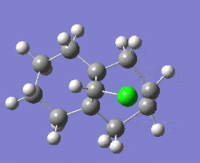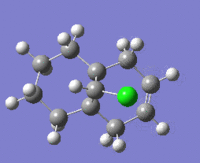
C=Canti	1737		N/A	N/A

Figure 13: The vibrational stretches and frequencies of 12 and 13.

By comparing the vibrational stretches for the two molecules we can see the clear differences caused by the overlapping of the σ* orbital. The C-Cl stretch occurs a lower frequency in compound 12 because the C-Cl σ* orbital donates electron density to the C=C π orbital and therefore weakens the bond and causes it to become weaker. The syn C=C bond in both compounds have similar vibrational stretches and as a result have similar bond strengthens as they are not significantly influenced by an other orbitals. This supports the MO diagrams drawn in the previous section. The anti C=C bond cannot be compared between the two compounds because the mono-unsaturated (compound 13) does not have a anti C=C bond but it is possible to compare with the syn C=C bond. The anti C=C bond has a smaller vibrational frequency and is therefore a weaker bond than the syn C=C bond. Therefore this supports the computational data which suggests that electron density is donated to the C=C π orbital from the C-Cl σ* orbital and therefore makes the bond weaker as the orbitals become more diffuse.

When the two C=C double bonds are analyised after the energies and geometries have been minimised there is a small difference in the two bond lengths, 1.336Â and 1.334Â. However this difference is not significant due to the approximations taken into account when calculating the geometries of the molecules. The distance between the bridging carbon and the corresponding carbon of each double bond is compared in order to investigate if each ring has similar dimensions. There was found to be a clear difference in the distance between the two rings. This effect can not be solely attributed to the C-Cl σ* orbital, the steric size of the chlorine atom will cause a change in geometry.

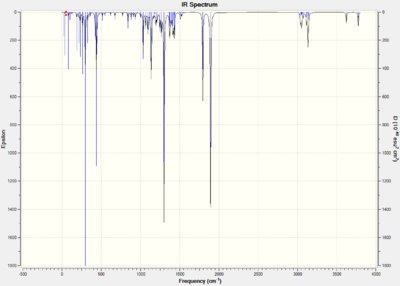
The infrared absorption spectrums can be modeled.

Compound 12	Compound 13
The IR spectrum of compound 12	The IR spectrum of compound 12

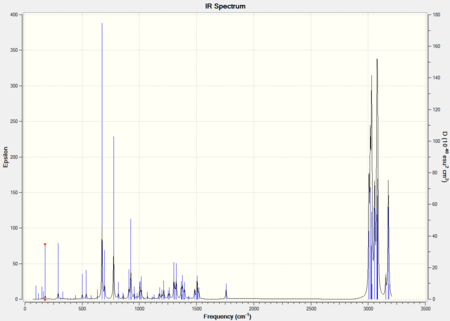Figure 14: The IR spectrums of compound 12 and 13.

By predicting the molecular orbitals of both the reactants we have been able to understand the regioselectivity of a reaction. MOPAC/AM1 modeling has allowed us to show the differences between two double bonds which look similar however react very differently.

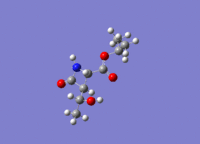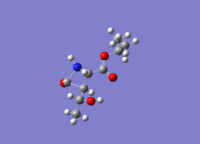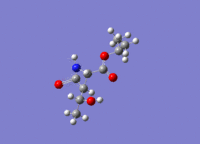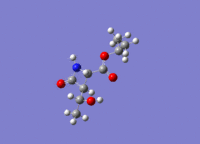
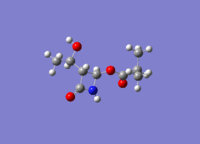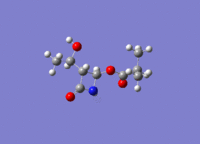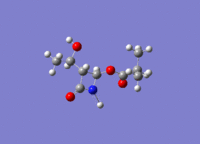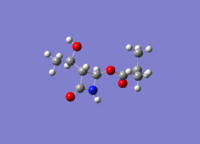
Gylcosidation

Gylcosidation is common reaction which occurs in nature and allows sugar molecules to polymerise. During a glycosylation the neighboring group effect, which relies on the stereochemistry of the compound, influences the reaction and means that the 1,2 trans product is formed exclusively. However the 1,2 trans product has two different conformers because the nucleophile can attack the intermediate from too different angles. Therefore there are two isomers of the intermediates labelled A, B, C D.

Figure 15: The reaction schemes froming the α and β anomers

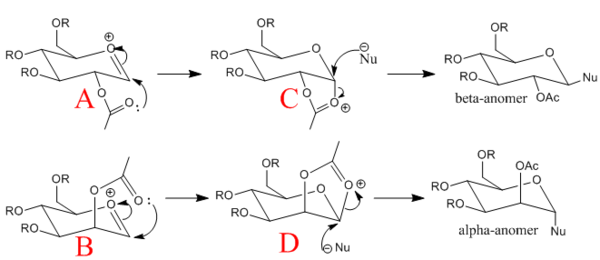
When modelling the intermediates methyl groups were used as the R groups because they are small and have few electrons (8 electrons vs. 19) which means less time is required to model the molecule. If a hydrogen atom is used instead of the a methyl group there added complications such as hydrogen bonding.

MM2 and MOPAC/PM6 methods are used to analysis the energies and geometries of all the complexes. Both these methods have there strengths and weaknesses for this sort of structure.

The MM2 method does not factor in the neighboring group effects of the acetyl group and the oxonium cation. This interactions is essential to predict the regioselectivity of the 5 membered ring which is formed. Also bond conjugation is not factored in as the acyl group is highly conjugated. Both these inaccuracies mean that there is a significant error when using this method.

The MOPAC/PM6 modelling does take into account the factors which the MM2 method does not and is therefore used to optimise the geometries of all the intermediates. The differences in structure can be seen from the structures produced by both methods.

Monosaccharide Energies

Compound	Energy (kcalmol-1) [MM2]	Energy (kcalmol-1) [MOPAC/PM6]	[MM2] optimised structure	[PM6] optimised structure
Monosaccharide A	24.9	-91.6
Monosaccharide A*	33.9	-77.4
Monosaccharide B	20.6	-88.7
Monosaccharide B*	31.6	-77.5
Monosaccharide C	26.7	-91.6
Monosaccharide C*	44.1	-67.0
Monosaccharide D	24.2	-84.5
Monosaccharide D*	46.8	-66.8

Figure 16: A table of energies for the monosaccharides A, A*, B, B*, C, C*, D, D* optimised using MM2 and MOPAC/PM6

Compound	Stretch (kcalmol-1)	Bend (kcalmol-1)	Stretch-Bend (kcalmol-1)	Torsion (kcalmol-1)	1,4- VDW (kcalmol-1)	Dipole/dipole (kcalmol-1)	Charge/Dipole (kcalmol-1)	Total Energy (kcalmol-1)
Monosaccharide A	2.89	11.6	1.09	3.60	18.8	-20.0	5.87	20.9
Monosaccharide A*	2.43	10.5	0.962	2.40	18.7	-2.90	4.34	33.9
Monosaccharide B	2.78	10.7	0.982	2.80	18.9	-21.8	5.53	20.6
Monosaccharide B*	2.47	10.6	0.894	0.598	18.4	-5.29	5.25	31.6
Monosaccharide C	1.97	13.3	0.686	8.00	17.7	-10.0	-2.33	26.7
Monosaccharide C*	2.73	21.0	0.881	7.36	18.0	-2.55	-1.12	44.1
Monosaccharide D	1.76	19.9	0.711	7.60	17.5	-21.6	0.485	24.2
Monosaccharide D*	2.87	18.7	0.905	9.05	19.0	-0.3778	-1.401	43.8

Figure 17: The split of energies of monosaccarides minimised using MM2

Analysis

The energies of the two isomers are found to be different depending on the orientation of the acetyl group above or below the plane. This is due to the interactions between the polar oxygen atoms as they will repel each other due to their electrostatic charge. This can be seen by the difference in the A Vs A* and the B Vs B* Dipole/Dipole values. This effect is not as strong in the C Vs C* and D Vs D* isomers but the C and D isomers are still the most stable conformations. Such a large difference in the energies of the most stable A, B, C and D compared to A*, B*, C* and D* means that the reactions will occur via the more stable intermediates and produce products which are nearly 100% abundant.

The MOPAC/PM6 modeling method was the most successful method and allowed us to conclude the differences between the isomers. It has shown that the orientation of the acetyl group around a ring has a strong influence on the energy of the molecule.

Investigating the regioselectivity of the Baeyer-Villiger reaction

A Baeyer-Villiger reaction occurs when a ketone or an aldehyde is treated with a peracid to form a ester; a lactone may be produced if the a cyclic ketone is used. The reaction occurs by the insertion of a oxygen between carbonyl carbon and the alpha carbon via an oxidative cleavage mechanism which is driven by the cleavage of the weak O-O bond and the forming of a strong C=O. The reaction is regioselectivity and steroselective of the reaction is due to the overlap of the orbitals which forms a stable the intermediate.

During the reaction the position of the orbitals must be taken into consideration. The first step of the reaction is a simple protonation of the ketone by the peracid, which leaves a positiivly charged oxygen and a negatively charged pereacid. The peracid can then nucleophilically attack the carbonyl carbon and break the carbon to oxygen π bond. This then mean that the carbon is sp³ hybridised and as a result some of the orbitals overlap to form a stable conformation.

Figure 18:Blue lines show antiperiplanar orbitals.

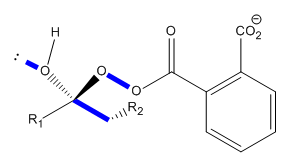
The orbitals shown in figure # show the orbitals which are antiperiplanar. Antiperiplanar orbitals have the best overlap between their orbitals and as a result have the largest stabilisation energy when they overlap.

The intermediate shown in figure # is common example of the Baeyer-Villiger reaction and is known as a Criegee intermediate. If the molecule involved is unsymmetrical two possible products could be formed. The product which is formed depends on the migrating aptitude of the ketone substituent.

Baeyer-Villiger reaction in the synthesis beta-lactam antibiotics

Figure 19:The reaction scheme for the synthesis of beta-lactam antibiotics

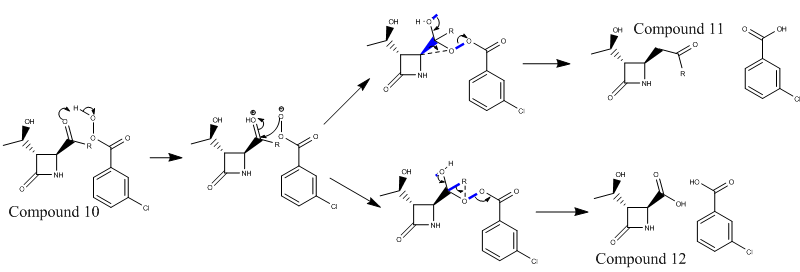
The reaction involves the movement of electron density from the lone pair on the oxygen to the antiperiplanar σ* C-C bond. The σ C-C bond also has an antiperriplanar relationship with the σ* O-O bond. These relationships are marked out on the reaction scheme by blue lines. The product depends on which C-C bond is broken.

The reaction shown above has two possible routes in order to form the products. The product which is formed has the most stable Criegee intermediate. The type of R group majorly effects the stability of the Criegee intermediate and therefore the the product.

As the R groups are changed the distribution of products changes.

• If R=^tBu the reaction is 100% selective towards compound 12 because the carbon the 3^o is good at stabilising the positive charge. The 3^o carbon is better at stabilising the positive charge because electron density is donated from three σC-H bonds to the empty p_vac orbital (Deslongchamps' theory - more steroelectronic interactions are better than one)

• If R = ⁱPr the R group is not as effective at stabilising a positive charge and as a result less of compound 12 would be produced. The reaction produces 52% compound 11 and 48% compound 12.

• If R = ^cPr (cyclopropyl)100% of compound 11 is produced because the two CH₂ groups next to the C which contains the partial positive charge are not in the correct orientation to donate electron density. The two σ C-H bonds are not in an antoperiplannar or periplannar arrangement so the orbital overlap is minimal.

• If R = Ph 100% of compound 11 is formed. This is not due to steroelectronic reasons state for the previous 3 groups , but instead it is due to the size of the phenyl ring.

To understand the regioselectivity of the reaction the ⁱPr R group is used as it produces a mix of products and therefore can show the small differences in the transition states. The conclusions drawn from this analysis can be expanded to be used to explain the other results.

NMR Analysis

The NMR chemicl shifts of a geometrically optimised structure can be calculated by a multistage process. Firstly the structure is minimised manually and using MM2, then using MOPAC followed finally using the Gaussian DFT optimisation method. The ¹³C NMR spectrums produced will not be perfect to the experimental values because approximations are made during the calculations, however they will give us an decent approximation of the chemical shifts.

Compound 11

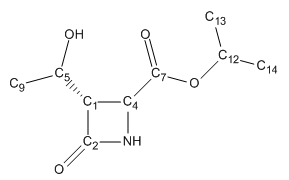
Figure 20: The labelled carbons of compound 11

The energy of compound 11 is minimised and the NMR spectrusm predicted using Gaussian. The chemical shifts are computed and shown in the table below. Some of the values need to be corrected because of there position within the molecule. The carbonyls of the esters and amides are corrected using a simple equation, δ_corr = 0.96δ_calc + 12.2. The error is a systematic error which is why it can be altered using a standard equation.

Carbon atom	δcalc (ppm)	δcorr (ppm)	δexp (ppm)	Percentage Difference
C14	20.04	20.04	18.8	+6.60
C13	20.16	20.16	18.9	+6.67
C7	23.06	23.06	21.3	+8.26
C12	37.99	37.99	34.0	+11.7
C1	63.00	63.00	63.9	-1.50
C6	66.18	66.18	65.2	+1.50
C4	77.99	77.99	75.9	+2.75
C2	157.9	163.8	167.2	+2.00
C10	172.6	177.9	177.6	+0.1

Figure 21: The ¹³C NMR chemical shifts for compound 11

The method used to predict the ¹³C NMR spectrums should product chemical shifts which are within 3-5ppm of the literature values. All the values obtained are within these limits allowed by the method. However the spectrum produced by Gaussian will be different to the experimental spectrum which would show carbon 13 and 14 in an identical chemical environment due to the rotation around the C₁₀-C₁₂ bond.

Compound 12

Figure 22:The labelled carbons of compound 12

The same procedure is used to minimise the energy of compound 12 as is used for compound 11. The same equation is used to correct the systematic error.

Carbon atom	δcalc (ppm)	δcorr (ppm)	δexp (ppm)	Percentage Difference
C14	21.3	21.3	21.3	0
C13	21.5	21.5	21.8	+1.4
C9	24.1	24.1	21.9	+10.0
C4	54.2	54.2	50.0	+8.40
C1	64.5	64.5	64.0	+0.8
C5	65.8	65.8	64.5	+2.0
C12	68.6	68.6	69.7	-1.68
C2	158	164	168.3	-2.49
C7	168	173	170.9	+1.2

Figure 23: The 13C NMR chemical shifts for compound 12

Similarly to compound 11 the chemical shifts are within the 3-5ppm error expected from the method used. The signals do not have the same deviation from the experimental value because the approximations used to calculate the chemical shifts will have different effects depending on on the environment of the atom. Again the NMR of the compound does not take into account any rotations of bonds or changes in structure and therefore shows two signals very close to each other.

By comparing the two NMR spectrums of compound 11 and 12 the differences in the chemical shifts for the two compounds can be seen. The major shift is in the central carbon of the ⁱPr R group. In compound 11 the chemical shift of C₁₂ is more shielded (downfield) because the carbon is bound to a carbonyl carbon, whereas the equivalent C₁₂ carbon found in compound 12 is more deshieled (upfield) because it is bonded to a electronegative oxygen.

Infrared Analysis

The infrared spectrums are shown below with some key stretches. The values for the stretches are 8% larger than expected. The values are therefore corrected to take this into account.

Compound 11	Compound 12
Figure 24: The infrared absorption spectrum for compound 11 after the energy has been minimised	Figure 25: The infrared absorption spectrum for compound 12 after the energy has been minimised

Bond	Structure 11				Structure 12
	Wavenumber of stretch/cm-1	Vibration	Stretch/cm-1corr	Stretch/cm-1lit	Wavenumber of stretch /cm-1	Vibration	Stretch/cm-1corr	Stretch/cm-1lit
C=O acetyl	1814		1669	1740	1794		1650	1721
C=O ring	1894		1742	1783	1893		1742	1749
N-H	3629		3339	3330	3625		3335	3330

Figure 26: The major stretching frequencies shown with there vibrations.

If the bond stretch is within 50cm^-1 of the literature values they are thought to be in good agreement. The values for the stretches of N-H and the C=O in the ring are therefore in agreement with the literature for both compounds however the acetyl C=O stretch does not agree with the literature. The two compounds are easiest to distinguish when the acetyl C=O stretch is investigated as it has the greatest difference between the two corrected stretches(1669, 1650 cm^-1). The method used to minimise the energy of the molecule and calculate the stretches is not able to fully model the conjugated nature of the bonds, this leads to the disagreement with the experimental values.

Mini-Conclusion

By analysing both the compounds by ¹³C NMR and infrared spectroscopy the differences between the two products can be seen. The most successful way to distinguish between the two compounds is to us NMR analysis. NMR analysis shows a shift of the chemical shifts between the two products as well as a significant shit for the central ⁱPr carbon. Although the ¹³C spectrum was accurate it did not show the distinguishable differences between the molecules. These differences would be shown if a ¹H NMR spectrum was calculated. The ¹H NMR spectrum uses the Karplus equation to calculate the ³J_H-H coupling constants, this is the simplest method. To find a more accurate measure of the coupling constants quantum mechanic methods can be used. The infrared spectrum as a whole does not change significantly however one of the stretches does move a significant amount.