Mod1598
Introduction to Molecular Modelling
NH3 molecule
Key Information
Calculation Method- RB3LYP
Basis set- 6-31G(s,p)
Final energy E(RB3LYP)- 56.55776762 au
RMS gradient- 0.00032440 au
Point group- C3V
Geometric Information
| Optimised N-H bond distance | 1.01865 Å |
| Optimised H-N-H bond angle | 37.126° |
'Item table' for optimisation results
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000070 0.001800 YES
RMS Displacement 0.000033 0.001200 YES
Interactive NH3 molecule |
The above JSmol image demonstrates the optimised NH3 molecule that was formed using GaussView. The link to the optimisation file can be found here.
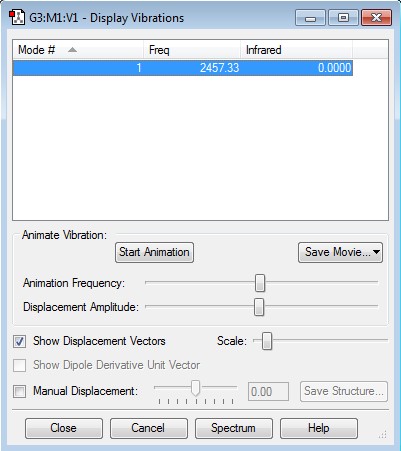
Display Vibrations for NH3
The above image shows that all vibrational frequencies are positive.
Answered questions on vibrations
- From 3N-6 rule, 6 vibrational modes are expected.
- The degenerate modes are mode 2 and mode 3, and mode 5 and mode 6.
- The bending vibrations are 1, 2 and 3, and the stretching vibrations are 4, 5 and 6.
- Mode 4 is the highly symmetric mode.
- Mode 6 is the "umbrella symmetric" mode.
- 4 bands should be seen in the experimental spectra of gaseous ammonia.
Charge Analysis
| Charge on N atom | 1.125 |
| Charge on H atoms | 0.375 |
Nitrogen would be expected to have a negative charge and hydrogen would be expected to have a positive charge. This is due to the greater electronegativity of nitrogen, leading to increased electron density surrounding the atom and therefore a negative charge on nitrogen, and a positive charge on hydrogen.
N2 molecule
Key Information
Calculation Method- RB3LYP
Basis set- 6-31G(s,p)
Final energy E(RB3LYP)- -109.52412868 au
RMS gradient- 0.00000003 au
Point group- DinfH
Geometric Information
| Optimised N-H bond distance | 1.10000 Å |
| Optimised H-N-H bond angle | 180° |
'Item table' for optimisation results
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Interactive N2 molecule |
The above JSmol image demonstrates the optimised N2 molecule that was formed using GaussView. The link to the optimisation file can be found here.
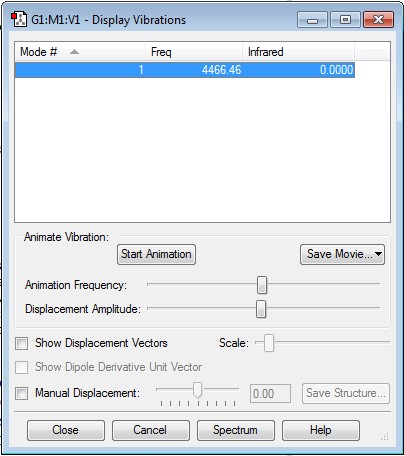
Display Vibrations for N2
No negative frequencies present
H2 molecule
Key Information
Calculation Method- RB3LYP
Basis set- 6-31G(s,p)
Final energy E(RB3LYP)- -1.17853936 au
RMS gradient- 0.00002276 au
Point group- DinfH
Geometric Information
| Optimised H-H bond distance | 0.74 Å |
| Optimised H-H bond angle | 180° |
'Item table' for optimisation results
Item Value Threshold Converged?
Maximum Force 0.000039 0.000450 YES
RMS Force 0.000039 0.000300 YES
Maximum Displacement 0.000052 0.001800 YES
RMS Displacement 0.000073 0.001200 YES
Interactive H2 molecule |
The above JSmol image demonstrates the optimised H2 molecule that was formed using GaussView. The link to the optimisation file can be found here.
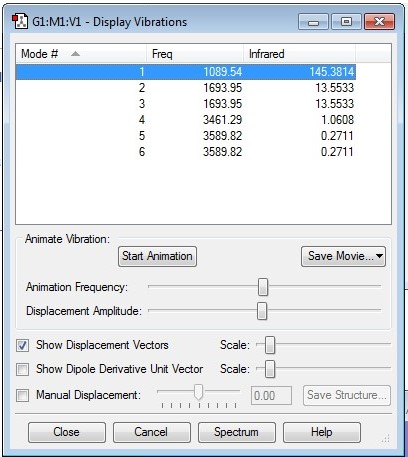
Display Vibrations for H2
No negative frequencies present
Reactivity of N2 and H2
Below are the energy values obtained from the above calculations, which I will use to calculate the energy change of the Haber-Bosch process:
E(NH3)= -56.55776762 au = -148492.43 kj/mol
2*E(NH3)= -113.11553524 au = -296984.86 kj/mol
E(N2)= -109.52412868 au = -287555.62 kj/mol
E(H2)= -1.17853936 au = -3094.26 kj/mol
3*E(H2)= 3.53561808 au = -9282.77 kj/mol
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -296984.86 -[-287555.62 + -9282.77] = -146.47 kJ/mol - This is the energy required for the conversion of hydrogen and nitrogen gas into ammonia gas. The ammonia product is more stable, as it has slightly lower overall energy than the two gaseous products.
Small Molecule Study- CH4
Key Information
Calculation Method- RB3LYP
Basis set- 6-31G(s,p)
Final energy E(RB3LYP)- -40.52401406 au
RMS gradient- 0.00000703 au
Point group- TD
Geometric Information
| Optimised C-H bond distance | 1.09190 Å |
| Optimised H-C-H bond angle | 35.264° |
'Item table' for optimisation results
Item Value Threshold Converged?
Maximum Force 0.000014 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.000038 0.001800 YES
RMS Displacement 0.000021 0.001200 YES
Interactive CH4 molecule |
The above JSmol image demonstrates the optimised CH4 molecule that was formed using GaussView. The link to the optimisation file can be found here.
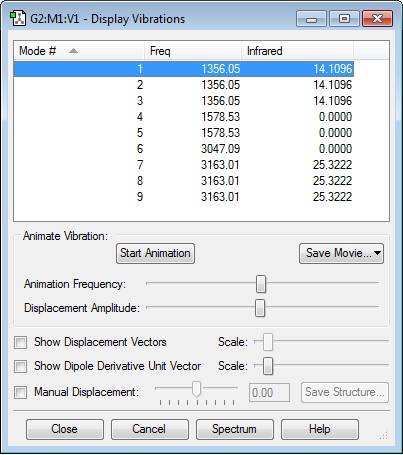
Display Vibrations for CH4
Information on vibrations
- As vibrational modes 1, 2 and 3, as well as 4 and 5, and 7, 8 and 9 are degenerate, a total of 5 bands in the experimental spectra would be expected.
- The bending vibrations are 1, 2, 3, 4 and 5, and the stretching vibrations are 6, 7, 8 and 9, with 6 being particularly symmetric.
- The 3N-6 rule predicts 9 vibrational modes for methane, which is the number present in the data.
Charge Analysis
| Charge on C atom | -0.930 |
| Charge on H atoms | 0.233 |
Carbon has a slightly higher electronegativity than hydrogen, so would be expected to have a negative charge due to increased electron density around the carbon.
Molecular Orbital Analysis




1. This molecular orbital is the lowest in energy of any, and the carbon 2s AO and a hydrogen 1s AO contribute to the MO. It is the bonding MO, and is the deepest in energy of any of the orbitals, and is therefore not near the HOMO/LUMO region. It is occupied by a pair of electrons, and has no effect on bonding.
2. This molecular orbital shown in the image is one of three degenerate orbitals, and is contributed to by the three carbon 2p AOs and three hydrogen 1s AOs. These MO's contain a nodal plane each. This MO is in the HOMO/LUMO region, and would be classed as the HOMO of the molecule, and is therefore likely to be heavily involved in bonding. The three MO's are occupied by 3 pairs of electrons.
3. The third molecular orbital is the antibonding orbital of the lowest energy MO, and formed from the same AOs. This MO is in the HOMO/LUMO region, and is considered the LUMO, once again resulting in a large impact on any bonding that methane takes part in. This MO is unoccupied.
4. The fourth and final molecular orbital is one of three antibonding orbitals that are formed from the same orbitals as the HOMO. These MO's are highest in energy of all the MO's, are unoccupied, and will be unlikely to have any effect on bonding.
An image of a fifth MO is unnecessary , as the other MO's calculated are degenerate to those above.
Independent Section
For the independent section of the wiki, I have completed a few additional calculations for another small molecule, H2O, in the table below.
Key Information
| Calculation Method | RB3LYP |
| Basis set | 6-31G(s,p) |
| Final energy E(RB3LYP) | -76.41973740 au |
| RMS gradient | 0.00006276 au |
| Point group | C2V |
| Optimised O-H bond distance | 0.96522 Å |
| Optimised H-O-H bond angle | 103.745° |
'Item table' for optimisation results
Item Value Threshold Converged? Maximum Force 0.000099 0.000450 YES RMS Force 0.000081 0.000300 YES Maximum Displacement 0.000128 0.001800 YES RMS Displacement 0.000120 0.001200 YES
Interactive H2O molecule |
The link to the optimisation file for H2O is here