Mod01559535
NH3
Molecule: ammonia Calculation method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP):-56.55776873 au RMS gradient: 0.00000485 au Point group: C3V N-H bond length: 1.02 Angstroms H-N-H bond angle: 106°
Interactive ammonia molecule |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
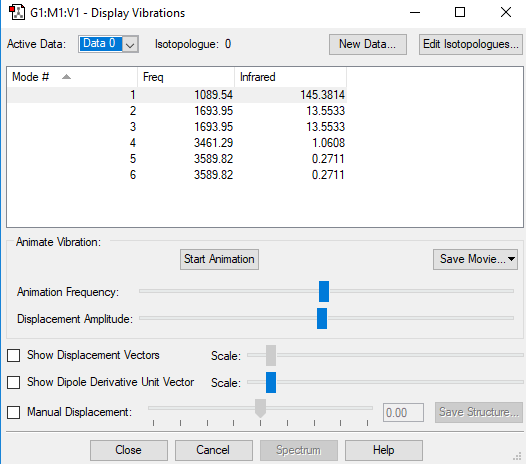
| Vibration number | Frequency (cm-1) | Intensity (arbitrary units) | Symmetry | Image |
|---|---|---|---|---|
| 1 | 1090 | 145 | A1 |  |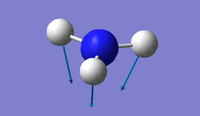
| 2 | 1694 | 14 | E |  |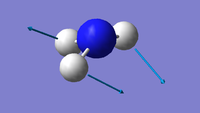
| 3 | 1694 | 14 | E |  |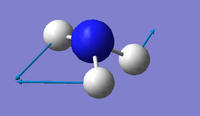
| 4 | 3461 | 1 | A1 |  |
| 5 | 3590 | 0 | E |  |
| 6 | 3590 | 0 | E |  |
Using the 3N-6 rule, 6 vibrational modes are expected, as 3(4)-6=6. There are two sets of degenerate modes; one set is at 1694 wavenumbers (modes 2 & 3) and the other set is at 3590 wavenumbers (modes 5 & 6) The modes at 1090 wavenumbers and 1694 wavenumbers (modes 1, 2 & 3) are bending vibrations and the modes at 3461 wavenumbers and 3590 wavenumbers (modes 4, 5 & 6) are stretching. The mode at 3461 wavenumbers (mode 4) is highly symmetric. The "umbrella" mode is at 1090 wavenumbers (mode 1) Two bands would be observed in an experimental spectrum of gaseous ammonia - although four different frequencies are observed in total, the stretching frequencies are of much lower intensity, therefore meaning only two bands would be observed.
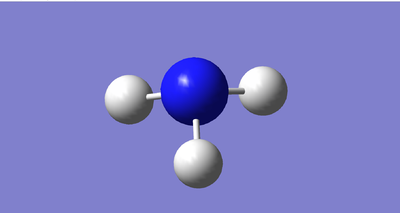
Shown above is an image of the charge distribution on an ammonia molecule. It is expected that the nitrogen is negatively charged and the hydrogens are positively charged - this is because nitrogen is much more electronegative than hydrogen, therefore nitrogen pulls the electron density towards itself.
Optimisation file can be found here
N2
Molecule: nitrogen Calculation method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP): -109.52359111 au RMS gradient: 0.02473091 au Point group: D∞H N-N bond length: 1.11 Angstroms The charges on both atoms are the same (0) because they have the same electronegativity, therefore the overall charge on the molecule is zero.
Interactive nitrogen molecule |
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
The optimisation file can be found here
H2
Molecule: hydrogen Calculation method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP): -1.17853936 au RMS gradient: 0.00000017 au Point group: D∞H H-H bond length: 0.74 Angstroms The charges on both atoms are the same (0) because they have the same electronegativity, therefore the overall charge on the molecule is zero.
Interactive hydrogen molecule |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The optimisation file can be found here
The Haber Bosch Process
The Haber Bosch Process is a process in which ammonia is formed from nitrogen and hydrogen. The equation for the reaction is shown below: N2 +3H2 --> 2NH3 E(NH3)= -56.55776873 au 2*E(NH3)= -113.1155375 au E(N2)= -109.52359111 au E(H2)= -1.17853936 au 3*E(H2)= -3.53561808 ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05632831 au ΔE=-147.9kJ/mol]
This process is exothermic, meaning the product (ammonia) is more stable as it is at a lower energy. A literature value for ΔE was found to be -92kJ/mol[1] - although this is exothermic and is similar to the value calculated in this aspect, the literature value and the value obtained from calculations still differ by approximately 55kJ/mol.
CH4
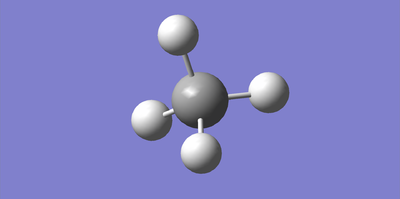
Molecule: methane Calculation method: RB3LYP Basis set: 6-31G(d,p) Final energy E(RB3LYP):-40.52401404 au RMS gradient: 0.00003263 au Point group: Td C-H bond length: 1.09 Angstroms H-C-H bond angle: 109°
Interactive methane molecule |
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.000179 0.001800 YES RMS Displacement 0.000095 0.001200 YES
| Vibration number | Frequency (cm-1) | Intensity (arbitrary units) | Symmetry | Image |
|---|---|---|---|---|
| 1 | 1356 | 14 | T2 |  |
| 2 | 1356 | 14 | T2 |  |
| 3 | 1356 | 14 | T2 |  |
| 4 | 1579 | 0 | E |  |
| 5 | 1579 | 0 | E |  |
| 6 | 3046 | 0 | A1 |  |
| 7 | 3162 | 25 | T2 | |
| 8 | 3162 | 25 | T2 | |
| 9 | 3162 | 25 | T2 | |
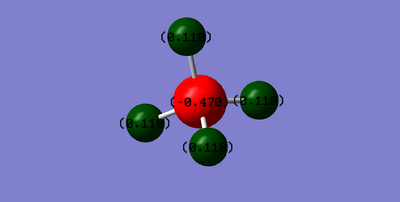
This charge distribution is as expected, as carbon is more electronegative than hydrogen and therefore pulls the electron density towards itself, creating a negative charge on the carbon and a positive charge on the hydrogen atoms.
Optimisation file can be found here
Molecular orbitals of CH4
Methane has 4 bonding and 4 antibonding molecular orbitals. The third, fourth and 5th molecular orbitals are all degenerate with energies of -0.38831. The HOMO is the sigma bonding orbital and has energy of -0.38831 and consists of 1s orbitals from hydrogen and 2sp3 orbitals from carbon. The HOMO can be considered to be any of the three degenerate occupied orbitals. The LUMO is the sigma star anti bonding orbital and has an energy of 0.11824 As the three orbitals (Figures 3, 4 and 5) are all degenerate, any may be considered the HOMO. All of the electrons occupy the bonding orbitals, therefore the antibonding orbitals do not contribute to the bond order. Methane has a bond order of 4, as 0.5(8)-0=4.
The optimisation file can be found here
Frequency tables for N2 and H2
| Vibration number | Frequency (cm-1) | Intensity (arbitrary units) | Symmetry | Image |
|---|---|---|---|---|
| 1 | 2457 | 0 | SGG |  |
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 0/1
Have you completed the calculation and given a link to the file?
NO - Your given link redirects to the .log file of an optimised N2 molecule
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 2/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES
You could have analysed the calculated vibrations as you did for NH3. You missed to explicitly state the occupancy and effect on bonding of all MOs. You correctly identified the contributing AOs for the HOMO. You commented on the LUMO without showing it. You showed two MOs which you never mentioned in your description (Figure 1 & 2). You missed to give the relative MO energies and to explain these as well.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
YES - you could have tried to explain why there is such a difference between experimental and computational values for the reaction energy of the Haber-Bosch-process.
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far
| Vibration number | Frequency (cm-1) | Intensity (arbitrary units) | Symmetry | Image |
|---|---|---|---|---|
| 1 | 4466 | 0 | SGG |  |