Mod.timarbab
Modelling Using Molecular Mechanics
The Hydrogenation of Cyclopentadiene
Dimerisation of cyclopentadiene
Cyclopentadiene can dimerise, in a cycloaddition reaction, to form two different stereoisomers. These are the endo and exo forms. The reaction is a cycloaddition reaction because it is forming 2 bonds between the ends of two pi systems. The reaction involves 6 electrons, therefore it is 4n + 2 = 6 where n = 1. The reaction proceeds via heat, and so the reaction will proceed with a suprafacial topology via a Huckle transition state. The exo form (1) is the form where both bonds form on the top face. The endo form (2) being the opposite, both bonds forming on the bottom face. Which of these two is preferentially formed was the question posed.
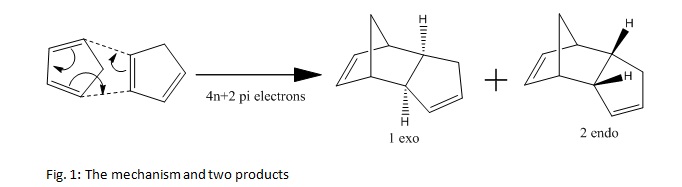
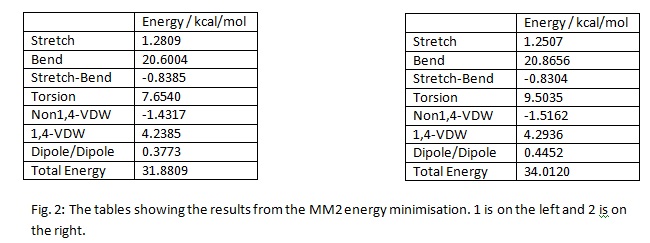
The two different products, 1 and 2, were modelled using ChemBio 3D Ultra 12. First they were drawn and rectified and then they were modelled using the MM2 force field. The results for these were given in the output and have been tabulated.
The energy minimization also produced a diagram of the molecule both as a 2-D representation filled and dashed wedges to indicate the positions in space of the atoms and as a 3-D picture. These pictures are below in the diagrams:
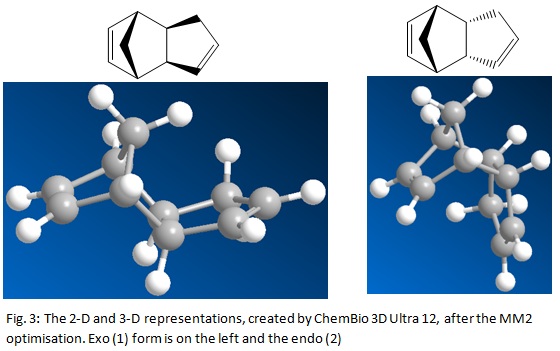
The total energy for 1 is lower than the total energy for 2. Therefore 1, the exo form, will be more stable. This means the exo form will be the thermodynamic product of the reaction. The endo form will therefore be the kinetic product of the reaction. Given the fact that the endo form is the observed product, the reaction must proceed with kinetic control. This means that the endo product is formed faster. This occurs because the transition state of the endo product is lower in energy than the corresponding transition state of the exo product.[1] The reason for the endo transition state being lower in energy than the exo transition state is primarily down to Secondary Orbital Interaction.[1] Some of the difference can also be due to the steric repulsion found in the exo transition state, between the methlene and the allyl.[1] The last of the two effects, i.e. the steric repulsion, contributes less than the Secondary Orbital Interaction.
Hydrogenation of the endo product
The endo product is unsaturated. It contains two double bonds. This means that hydrogenation can occur at either, or indeed both, of these sites. If a milder reducing agent is used, the site that is preferentially hydrogenated depends on the stability of the product formed. Once more ChemBio 3D Ultra 12.0 was used to model the two molecules. Both molecules were then, as before, optimised using the MM2 force field. The data produced from this was then tabulated and is displayed below:

Once again, this produced a 2-D and a 3-D visual representation of the molecules. These are shown below:
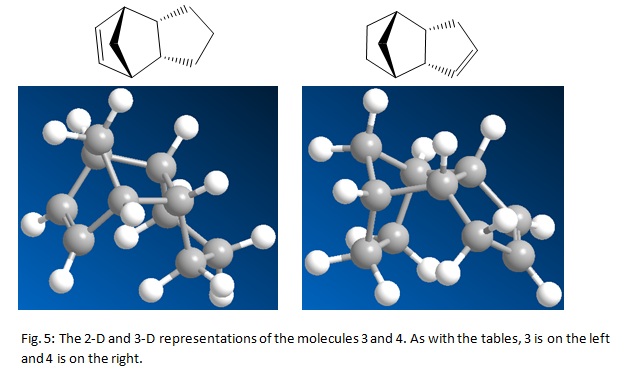
The lowest in energy of the two products of hydrogenation is molecule 4. This is 4.5270 kcal/mol lower in energy than 3. This means the thermodynamic product of the hydrogenation is molecule 4. For molecule 3 the stretching and the bending contribute a large amount to the total energy. In both cases, the stretching frequency is the largest contribution to the total energy. In both cases it contributes almost half to the total energy. The bending energy for 3 was considerable higher than the corresponding value for 4. This can clearly be seen in the table. This value is so large because of the bridging methyl group. It is much higher for 3 because a larger ring strain is produced by the C=C bond being in the 6 membered group that resembles norborene. This helps to explain why this bond is reduced first. It is the least stable and so will be reduced before the other double bond. As expected, in both cases, the contribution of the Dipole/Dipole interaction was very little. This is because the molecule is made up carbons and hydrogens. A C-C bond is actually not very polarisable. C=C bonds are more polarisable. However, the absence of a heteroatom, for example oxygen or nitrogen, means that the Dipole-Dipole contribution will be very low. In both cases, the torsional energy was the second largest contribution to the total energy. This was lower for 3 than 4. This was most likely because of the difference in position of the double bond. The molecule 4 will be more rigid than 3, therefore will have a larger contribution to the total energy from torsional energy. 1,4-Van der Waals interaction was the third highest contribution for both 3 and 4. This was because the position of the atoms in question was in the distance that was in the non attractive zone. The non 1,4-Van der Waals interactions were both attractive and fairly small. This suggests that the molecules are in a position such that these atoms are at a distance where they attract each other.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring
Reaction of prolinol with MgMeI
The reaction in question ends with alkylation of the 4 position on the pyridine ring. The mechanism, or proposed mechanism to be more precise, is written below.

ChemBio3D Ultra 12.0 was used to draw the molecules and then optimise to the lowest energy using the MM2 force field. For the first reactant the MeMgI was not included. The reason for this was the magnesium atom. The magnesium is not supported in MM2 and therefore the program will not be able to process it. The energy was minimized for molecules 5 and 6 using the MM2 force field. This produced a value for the energy of: 43.1695 kcal/mol with a dihedral angle of 7.5047°. This means that the oxygen atom is 7.5047 degrees above the heteroaromatic ring. The MgMeI will be bonded to the oxygen. The oxygen will be donating its lone pairs, located in an empty p orbital, to the Mg atom in the MgMeI. This is how the reaction is stereocontrolled. The Me will only attack from the face that the Mg is attached to. This means only one product, i.e. one stereoisomer, will be produced.
Nucleophilic addition of NHPhenyl group to a pyridinium ring
This reaction mechanism is shown below:
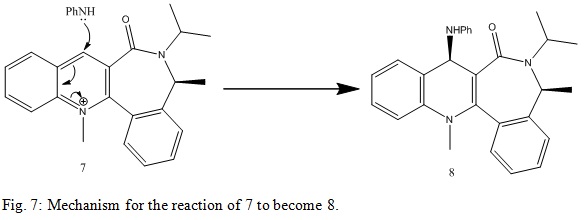
Once more 7 and 8 were minimised in energy using MM2 in ChemBio3D Ultra 12.0. The energies and angles were minimised to: 62.7130 kcal/mol and -22.9941°. Again, this angle directs the stereochemistry of the final product. The orbitals on the N atom and the O atom will not be close together as this would be unfavourable. The Ph group on the N makes the HNPh sterically bulky. This makes the product very favoured. This is why only one stereoisomer is produced. The stereoisomer produced also avoids any unfavourable interactions via overlap of the lone pairs on N and O in C=O. This is why the dihedral angle will actually be fairly large. This is shown in the result produced here.
Below are jmols of 5, 6, 7 and 8:
| Molecule 5 | Molecule 6 | Molecule 7 | Molecule 8 | ||||||||||||
|
|
|
|
- Fig. 8: Interactive Jmols of molecules 5-8.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The two molecules 9 and 10, shown in the diagram below, are two atropisomers of an important intermediate in the synthesis of the, extremely useful, molecule taxol:[2]

In the molecule 9 the carbon ring is a twist boat. In molecule 10 the carbon ring is a chair.[2] The molecular structures clearly show that there is one distinctive difference between the two. That is, of course, the orientation of the C=O. These two molecules were modelled with ChemBio3D Ultra 12.0. They were then minimised in energy using both the MM2 and MMFF92 force fields. These produced the same, relative, result. However the actual numbers they produced were fairly different. This is, of course, to be expected as they are different and so will make slightly different assumptions. Below is a table with the information calculated:
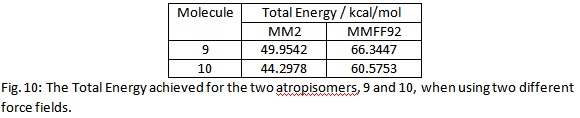
Molecule 10 is the most stable, from the information given in the table. This is possibly because molecule 9 will have a large amount of unfavourable interactions between the, electron rich, C=O and the bridging group next to it in space (on the left on the diagrams). This is avoided in molecule 10 by the C=O pointing down.
Below are the jmols for 9 and 10:
| Molecule 9 | Molecule 10 | ||||||
|
|
- Fig. 11: The Jmols for the two atropisomers 9 and 10.
The alkene reacts very slowly in both cases because it is a hyperstable alkene.[3] This means it will not readily be reduced to the corresponding alkane. This is probably because the alkane would have a much higher energy. In fact, the energy for the corresponding alkane of molecule 10 was actually minimised using MM2 and MMFF92. In both cases the energy comes out at significantly higher than the total energy for molecule 10. These are 79.0703 kcal/mol using MM2 and 114.817 kcal/mol for MM2. Therefore the much more stable form will be the alkene, molecule 10. Therefore it will not readily be reduced to form the corresponding alkane. Below is the Jmol for the corresponding alkane:
| Alkene product from hydrogenation of Molecule 10 | |||
|
- Fig. 12: The alkane related to molecule 10.
Modelling Using Semi-Emperical Molecular Orbital Theory
... RM1 is better
Regioselective Addition of Dichlorocarbene
The molecule under investigation here is molecule 12. The structure of this is shown, as a Jmol, below:
| Alkene product from hydrogenation of Molecule 10 | |||
|
- Fig. 13: A Jmol of molecule 12.
A key reaction, demonstrating the consequences of the orientation in space of various MOs, is the addition of dichlorocarbene to molecule 12. This has very high selectivity, indicated on the diagram below: [4]

The reaction above demonstrates which of the two alkenes is more nucleophilic. The dichlorocarbene is acting as a nucleophile in this instance. As can be seen, clearly the syn alkene is the most nucleophilic. If it wasn't, it would not be the dominant product. To put this into non scientific jargo: If the CCl2 group had gone onto the right it would show that the double bond on the right is the more nucleophilic. However, it went on the left and therefore the double bond on the left must be the more nucleophilic.
The molecule was drawn into ChemBio3D and the energy was optimised using the MM2 force field. This gave the total energy as: 17.9126 kcal/mol. The energy was then optimised using PM6 and the molecular orbitals were displayed. The PM6 minimisation gave a minimum energy of: 19.74037 kcal/mol This produced the orbitals shown below:

Note that the colours of the orbitals has been changed for clarity as the standard is a dark blue. The rather fetching electric blue is now representing that phase of the orbitals. The red remains unchanged. The HOMO shows that the bulk of the electron density is located on the side where the Cl is. This means that the nucleophile will attack the other side. The pi orbital on the double bond anti alkene side can take part in an interaction with the σ*orbital of the C-Cl. This is the HOMO-1 and the LUMO+1. This has the effect of producing two new orbitals. One is stabilised, with respect to the π orbital, the other is destabilised, with respect to the σ* orbital. This has the effect of overall stabilising the molecule. It also, more importantly in this application, has the effect of helping to direct attack to the other side. This is because the anti alkene bond will be made stronger, as it is made more stable An interesting point to note is that the dichlorocarbene is actually ambiphilic. That is to say it can act as both a nucleophile and an electrophile. This is because it has a vacant p orbital to accept electrons into while also possesing a lone pair of electrons. The former making it electrophilic, and the latter making it nucleophilic.
The Calculation was also run using RM1 as the method instead. This produced the molecular orbitals shown below:
PUT IN THAT PICTURE ONCE FINISHED IT
References
- ↑ 1.0 1.1 1.2 P. Caramella, P. Quadrelli, L. Toma., J. Am. Chem. Soc., 2002, 124, 7, pp. 1130–1131.[1]
- ↑ 2.0 2.1 S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, pp. 319.[2]
- ↑ W.F. Maier, P.V.R. Schleyer, J. Am. Chem. Soc., 1981, 103, pp. 1895.[3]
- ↑ B. Halton, S. G. G. Russell. J. Org. Chem., Vol.56,No.19, 1991, pp. 5553–5556.[4]
