Mod.2jlm07

Module 2: Inorganic Computations

Gaussian can be used to analysis and predict electronic and structural properties of molecules and hence predict thermal stabilities. This project practises the use of optimisating molecules to their lowest energy state, generating molecular orbitals, vibrational frequencies, and NBO analysis (Natural Bond Orbitals) by investigating Borane, Trichloroborane, Molybdenum isomers, and my own project on benzene, borazine and their derivatives.

BH₃ Opimisation

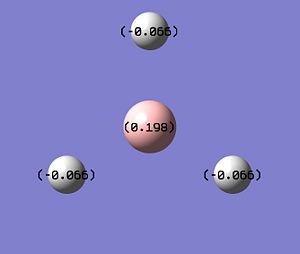
Gaussian was used to draw BH₃ and set the bond lengths to 1.5Å. An Optimisation Calculation was run using the Gaussian parameters #b3lyp/3-21g geom=connectivity. This refers to the type of method run, B3LYP, and the basis set, 3-21G. The method run links to the type of Hamiltonian approximation made and the basis set refers to the accuracy of the calculation e.g. the electronic structure of B in its ground state is 1s², 2s², 2p¹, therefore the 3 is related to 3 Guassian calculations linked with 1s², the 2 is related to 2 Gaussian calculations linked with 2s² and the 1 is related to 1 gaussian calculation linked with 2p¹. The calculation took 27secs to run and the resulting optimised bond lengths were 1.19A, bond angles were 120⁰, and dihedral angle was 180⁰. Since the run was very quick, this means only few iterations were needed to generate the lowest energy state, usually typical of small simple molecules. Since the bond angle made perfectly matches the trigonal planar structure of BH3, this highlights the accuracy of gaussian for simple molecules and the structure of the molecule. The bonds are single bonds, and the angles relate to the optimum sp² hydridised central Boron atom (this will be discussed shortly in the NBO analysis section) forming a trigonal planar molecule. Furthermore, the symmetry of the molecule is calculated in the simulation to give D3h. The summary of optimised energy can be seen in Fig.1.

Fig.1.BH3 Optimised Energy

The out log file for the optimisation can be viewed at https://www.ch.ic.ac.uk/wiki/index.php/Image:JEMMA_BH3_OPT.LOG

So, you can see the optimised energy is -26.4623a.u and there is no dipole moment to this fully symmetrical molecule. The energy can only be written accurately to 4 d.p. due to the conversion into Kcal/mol; the accuracy is to 10Kcal/mol, which is equivalent to 0.003809a.u.

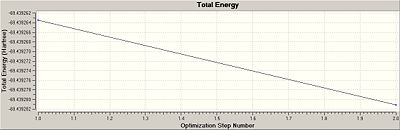
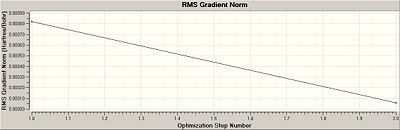
So, how does the calculation work? The optimisation acts to lower the energy of the molecule to its lowest possible state by trying to reduce the forces between the nuclei and electrons to zero by approximating a solution to the Schrodinger equation. That is the gradient of the internuclear distance v's potential energy graph reduces to zero, a stationary/turning point. This can be shown graphically from the optimisation calculation, Fig.2 and 3.

Fig.2.TE of BH3 during optimisation

Fig.3.RMS of BH3 during optimisation

The RMS is the root mean square (or average) or the gradient calculated over the optimisation period. This means it is showing the average deviation from the optimum bond length, so as it reduces to zero, the deviations reduce to zero. You can see from the summary the gradient is 0.0002a.u. to 4.d.p. You can see that as the Total Energy reduces to 26.4623a.u as the gradient reduces to zero. The images of the molecule throughout each of the 4 steps to ultimate optimisation are shown below:

1

2

3

4

You can see how the distance between the B and H atoms change as the energy is reduced to its optimum internuclear distances. Next, the Molecular orbitals will be looked at (see below).

BH₃ Molecular Orbital Calculations

Calculating the Molecular Orbitals using the checkpoint file from the optimised energy as the input file, gives the following out log file, DOI:10042/to-2979 . The basis set used here is to the same level of accuracy as the optimisation to avoid excited electron density and the key words "pop=full" was added to change to MO mode. Furthermore, NBO (Natural Bond Order) was set to "full NBO" to produce all the MO's. This calculation took 0.4secs to run on SCAN and 3secs on gaussview. Opening the checkpoint file of the results, going to edit, and MO's, visualise and selecting occupied (as well as the first 8 orbitals), and finally updating, the energies of the MOs 1-8 can be viewed, Fig. 4, as can the pictures of the MOs themselves, Fig.5.

Fig.5 MO diagram for BH3 with computed MOs and theoretical MOs

Fig.4.BH3 MO's 1-8

HOMO-4 (orbital 1) corresponds to the 1s non-bonding B orbital (1a'₁) that lies too deep in energy to take part in any reactivity and hence is not included in this valence MO diagram. Orbital 2 is made up from the s orbitals of the 3H fragment and the s orbital of the B fragment. Since the hydrogen fragment is closer/deeper in energy to the Boron, they contribute most to the MO, hence the larger coefficients being on the H's in the LCAO MO. Comparing the rest of the orbitals in a similar way, the HOMO, which is degenerate, has a slightly larger, but pretty much the same contribution from the H's and B, the LUMO is non-bonding so only has B contributions (the Gauss view image is actually a p orbital its just the other phase is behind it in the image), and the anti bonding orbitals have more B character. The non bonding rather than antibonding nature of the LUMO means it is lower in energy than antibonding orbitals and hence why B is electropositive. The energies of the orbitals increase due to the number of nodes in the MOs; the more nodes, the higher the energy e.g the HOMO has 1 node (for each orbital) and the antibonding orbitals have 3. Notice also that the anti-bonding orbitals have a positive energy whereas the bonding orbitals have a neagtive energy. This highlights how much higher in energy the anti-bonding orbitals are and hence why they are open to attack. Furthermore, notice how the bonds are not drawn on the molecule. This does not however mean the bonds are not there; if they were not there then the MO's would not be generated. In terms of Gauss view the bonds will only be present when the atoms are within a significally close proximity, dictated by the parameters of gaussview. When outside these parameters the bonds are not shown.

You can see that all the Gaussian calculated orbitals correlate nicely with the LCAO method in terms of both the phase pattern and number of nodes. Perhaps the only difference is the electron density about a particular atom. The LCAO appears more concentrated about a certain atom whereas the Guassian calculation is alot more diffuse and spread over the molecule. Also notice that the top 2 antibonding orbitals are of the same symmetry and fairly close in energy; this means they are susceptible to being the otherway round. Usually the a1 orbitals are lower in energy than e1 hence why it has been calculated this way round, but because s-s interactions are stronger than s-p interactions this can be the other way round. Overall, the methods are in good agreement and therefore are a very good way to start when wanting to discuss, determine, or explain the reactivity of a molecule.

BH₃ Natural Bond Orbitals Information

Fig.6.Atomic charges on BH3

The MO diagram above suggests the relative contributions that each fragment contributes when making up a MO. This can be more quantitatively analysed from the Gaussian calculation. Using the log file from the MO calculation, information about the atomic charges and % contributions from individual atoms that actually make up bonds can be made by running a NBO calculation. Selecting the charge distrubution option, the charges for the atoms can be viewed, Fig.6. This shows how the Boron is electropositive (positively charged) compared to the Hydrogens that are negative. This means the Hydrogens hold more electron density in the bonding orbitals whereas the Boron has more of an orbital contribution to the antibonding orbitals. Running the NBO calculation by selecting 'full NBO' the out file can be opened and the NBO data analysed.

Since Gaussview is not sophisticated enough to graphically interpret all the NBO information, the file can be viewed by going to 'results' and 'view file' and the following information obtained, Fig.7-10.

Fig.7.The Summary of Natural Population Analysis

Fig.8.Bond orbital/coefficient/hybrid

Fig.9.Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis

Fig.10.Natural Bond Orbitals (Summary)

Fig.10.Natural Population: Natural atomic orbital occupancies

Fig.7 shows how the natural charge is distributed on the atoms , how the boron is electropositive (and hence Lewis acidic), and how all the H's are electronegative in equal amounts. The overall total is zero, showing how all the charges balance out and there is not overall dipole.

Now relating back to the MO diagram, the relative contribution that each atom has to a MO can be seen quantitatively in Fig.8. Some of the figures have been hightlighted in the boxes; Bonding orbital 1, has an occupancy of 1.98, i.e. 2 electrons exist in that orbital, it has a relative B contribution of 46.65% of which 33.33% is 1s character and 66.67% is p character, and relative H contribution of 53.35%, of which 100% is s character. Bonding orbitals 2 and 3 are the same since all the bonds are equal. Bonding orbital 4 is the CR or Core electron orbtial and relates to the non-bonding B 1s orbital (100% B). Finally the 5th bonding orbital is LP* or the Lone Pair/antibonding orbital. You can see this has 0.0000 occupancy and is 100% boron.

Fig.9. outlines interactions between MOs mixing. This is not of interest here since all the numbers are below 20kcal/mol. Instead, of more interest is Fig.10. This highlights the positioning of the LUMO of the system. The LUMO is pAO of the Boron and should appear as the orbital of lowest energy with zero occupancy. In this case it is orbital 8 at -0.08090a.u. This is a negative number highlighting the very low lying character of the obital (usually unoccupied orbitals are positive) and the lewis acidic character of the molecule. Finally, this can be further shown in the Natural Population: Atomic orbital occupancies section of the file, to show how the pz orbital is empty, Fig.11.

BH₃ Frequency Calculation

So far, the energy of BH ₃ has been minimised finding the first derivative of internuclear distance v's potential graph. Therefore, the information obtained only informs us of the slope, but not whether your at a maximum or minimum point; you have to take the second derivative to obtain this information; positive value implies minimum; negative implies maximum. To achieve this, the frequency analysis can be run which is essentially the second order derivative of the potential energy surface (PES). All positive frequencies implies minimum, one negative implies transition state, and more than one negative implies the calculation has failed. Furthermore, the vibrational and ramon modes are calculated, which can then be compared with experimental data. The Optimised energy file must be used to calculate the vibrational frequencies. When opening the file, the 'read intermediate geometries ' box is unticked and a frequency calculation run; the summary is shown below, Fig.11.

Fig.11.Frequency Summary

Notice how the Total Energy is still the same as the original optimised energy as that seen in Fig.1 meaning the structures of the molecules are the same.

Since calculation was run on gaussview rather than SCAN, the log file for this calculation can be accessed on the following link https://www.ch.ic.ac.uk/wiki/index.php/Image:JEMMA_BH3_FREQ.LOG. The calculation took 10secs to run. The 'low frequencies' are the important results on the log file, representing how accurate the calculation is (Fig.12); they correspond to the '-6' centre of mass vibrations in the 3N-6vibrational modes for a non linear molecule and the closer to zero they are, the more accurate the calculation. You can see these are quite close to zero, but some reach up to about 66cm-1. This is due to the low basis set used of quite low accuracy. Also in the image are the vibrations 1-6 with their frequencies of vibration and symmetry group. This information is also highlighted and summarised in Table 1.

Fig.12.Low Frequencies generated of BH3

"Table 1: Vibrational modes of BH3 molecule"

Number	Vibration	Frequency/+/-10cm-1	Intensity	Symmetry point group
1	Wagging	1144	93	a2
2	Scissoring	1203	12	e'
3	Rocking	1204	12	e'
4	Symmetrical Stretching	2598	0	a'1
5	Assymmetrical Stretching	2737	104	e'
6	Assymmetrical Stretching	2737	104	e'

Since all the frequency values are positive, the optimisation calculation completed successfully and we are at the correct minimum energy.

All the values are rounded to the nearest whole number because of the low level of accuracy of the calculation. There is a systematic error of 10% because the calculation is run as a harmonic approximation for vibrations that are actually anharmonic. This 10% error leads to a 10cm^-1 for frequencies of the magnitude of 100cm^-1. Furthermore, the intensity values are even less accurate than the nearest whole number but they are written like this for convention.

You can see that the symmetric symmetry labels (a') match symmetric vibrations and the assymmetric labels (e') match the assymmetric vibrations. The vibrations that require more energy absorb at a higher frequency, namely the symmetric and assymmetric stretching. The intenstiy of the stretches is quite important also, the assymmetric vibrations are more intense whereas the symmetric vibration has an intensity of zero. This highlights the symmetry of the vibration cancelling out and hence not leading to any light absorption. Similarly, the intensity of 2/3 is also quite low, again due to the rocking motions cancelling each other out. This can be observed in the IR spectrum is shown below that only has 3 peaks. Vibrations 2 and 3 absorb at the same frequency, 4 has no intensity, and 5 and 6 absorb at the same frequency.

Calculations on BCl₃

Optimisation

Before any calculations regarding the BCl₃ molecule can be made, the molecule must be optimised to its most stable, lowest energy conformation. This was done using the following Gaussian information, Fig.1.

Fig.1.Optimisation Summary

The optimisation here is different from that used in BH₃ due to the increase in electron density (and mass) in the system when changing from H to Cl. To account for this the basis-set is changed to a pseudo-potential. This is a medium level of accuracy compared to the lower level of accuracy for BH3 and wont take too long to run. Furthermore, prior to this calculation, the symmetry of BCl₃ is restricted by clicking on the 'edit' tab, 'point group', 'enable point group symmetry' and constrain the point group symmetry to D3h. The tollerance level is then changed to 'very tight (0.0001)'. This calculation only took 6secs to run.

Note that the optimised energies retrieved from the borohydride molecule and borotrichloride molecule cannot be compared since they are not related; they are different molecules with different levels of accuracy due to the change in atoms, and have different basis sets used to run them.

The graphs showing the progress towards the minimised energy can also be shown in graphical format as the BH₃.

You can see here how the optimisation only has two steps and goes straight from its highest energy point (-69.4393a.u) to its lowest energy (-69.4393a.u) with no intermediate geometries. Notice, how, to 4 d.p. these values are actually the same; this suggests upon restriction to the D3h point group, molecular deviations about the equilibrium nuclear bond distance is strongly prohibited.

The out log file can be viewed from the link here https://www.ch.ic.ac.uk/wiki/index.php/Image:JEMMA_BCL3_OPT.LOG

Viewing the resulting out log file in gaussview and selecting the appropriate bond distance and bond angle buttons, the following lengths and angles are:

• Optimised B-Cl bond = 1.87Å
• Optimised Cl-B-Cl bond = 119.999 = 120⁰

Comparing this to the literature values of 1.72Å and 120⁰ shows that the calculation is fairly accurate, but a slight overestimate of the bond length. This is also shown by the animation of the molecule once optimised. All my bonds appeared in the animation screen once the molecule was optimised but sometimes this does not occur. Gaussview can sometimes appear to 'break bonds' between atoms as the bond lines disappear following a calculation. However, this doesnt mean there is no bond present, it just means that the distance set in guassview to imply a bond exists, has been exceeded and hence accordoing to gaussviews parameters, there is no bond present. Since the optimised bond distance for BCl3 lies within these parameters so the bonds appear.

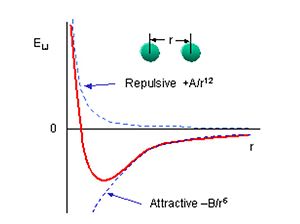
Furthermore, this leads us to the question of what is a bond? It is an electrostatic interaction between two opposing forces, i.e. a nucleus and electron, and hence is also known as a dipole interaction. It is formed when 2 electrons are placed between two nuclei within a close enough proximity to form a more stable, lower energy state than when further apart. If they become too close, the electrons repel and the atoms will fly off to infinitely, and if they move too far apart, the bond will eventually break to leave the atoms separate and existing at a higher energy state. This is depicted below :

potential energy v's interatomic distance

The symmetry expected from the ground state according to VSEPR is D3h. Since the calculation was actually restricted to a D3h point group this means the calculation may have fallen into a local minima rather than the lowest possible minimum. However, this minimum can be confirmed by running a frequency analysis as before and checking if all the frequencies obtained are positive. If they are, then we have reached the optimum geometry even if the molecule was restricted, confirming that D3h is actually the ground state structure.

Frequency

The optimisation file is used to run the frequency calculation so that the same method and basis set is used with the optimised molecule so they are to the same level of accuracy.

The out log file can be viewed on the link here https://www.ch.ic.ac.uk/wiki/index.php/Image:JEMMA_BCL3_FREQ.LOG This calculation took 11secs to run.

As before, the total energy of the molecule was the same as that of the optimisation confirming the same structural outcome. The relevant section, of the log file that shares the frequencies of vibrations and how accurate the calculation is, is shown below:

section of BCl3 IR out log file

Again, there are 6 modes of vibration as with the BH3 molecule which has the same shape. Looking at the low frequencies, the accuracy of the calculation seems better than that of the BH3 calculation, all the values are alot closer to zero. This is because the basis set is of medium level rather than the lower 3-21G used for BH3. The vibrations highlighted in the boxes are all positive and hence the optimised geometry has been reached. Gaussian is obviously good at predicting VSEPR. These vibrations are also highlighted next to their corresponding animation in the table below:

"Table 1: Vibrational modes of BCl3 molecule"

Number	Vibration	Frequency/+/-10cm-1	Intensity	Symmetry point group
1	Scissoring	214	4	e'
2	Scissoring	214	4	e'
3	Assymmetrical Stretching	377	44	a2
4	Symmetrical Stretching	417	0	a'1
5	Assymmetrical Stretching	259	104	e'
6	Assymmetrical Stretching	259	104	e'

Again, two pairs of vibrations absorb at the same frequency as their vibrations are very similar in energy. The intensity of the scissoring is low as they almost cancel each other out. The symmetrical stretching is of zero intensity as it completely cancels out. The IR spectrum with the 3 observable peaks is shown below:

BCl3 IR spectrum

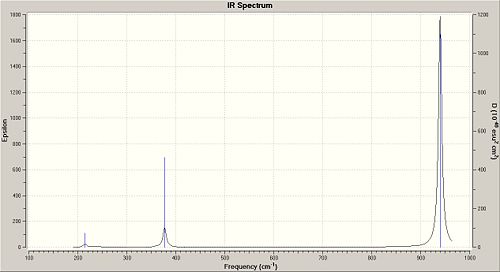
Isomers of Mo(CO)₄(PCl₃)₂

Optimisation

In this section IR spectra/frequency analysis will be used to distinguish between the two isomers of Mo(CO)₄(PCl₃)₂, cis and trans, and determine there thermal stabilities. The number of vibrational bands should change for the C=O ligand in the isomers; for the cis, it is expected that 4 vibrational peaks will be observable, and for the trans only one. This is due to the symmetry of the molecule; the trans vibrations cancel out due to the lack of dipole moment compared with the cis. Usually, this calculation would be run with phenyl groups, but due to the time it would take for these calculations to run, chlorine atoms are replacing these large, sterically hindering rings. Due to this increased rotation in the molecule from smaller chlorine atoms attached, and the fact that the molecule can actually exist in two stable conformations, we need to be more accurate and precise when running an optimisation to prevent falling into a local minimum. Furthermore, the increase in weight of the atoms used increases the number of orbitals that need to be considered in a calculation. Again, this means higher accuracy is needed and hecne a higher basis set will be used. First, the conformatons of each the cis and trans will be drawn in gaussview and a low basis set calculation will be run; B3lYP/LANL2MB with additional keywords 'opt=loose'.

The loose calculation for the cis isomer can be found here DOI:10042/to-3060 and for the trans isomer DOI:10042/to-3061 . These calculations took about 5 minutes to run each.

Taking the optimised file, the atoms for each conformer can now be moved to there most cis and trans positions and a more accurate optimisation run. For the cis conformer, the chlorine atoms wer moved sufficiently so one points up and one points down parallel to the axial bond. This was done by selecting the Cl-P-Mo-C dihedral angle and setting it to 0⁰ and 180⁰ respectively. For the trans conformation, it was ensured that both PCl₃ were eclipsed and and that one Cl atom from each group lies parallel to the Mo-C bond. This was again done by selecting the dihedral angle but this time setting it to from 60⁰ to 0⁰. The more accurate pseudo-potential was now run as LANL2DZ and a tigher conversion criteria was added in the additional keywords as 'int=ultrafine scf=conver=9'.

The ultrafine calculation for the cis isomer can be found here DOI:10042/to-3062 and for the trans isomer DOI:10042/to-3063 . These calculations took about 20 minutes to run each.

Finally, to further increase the accuracy and include the Phosphorus's low lying dAO's in the calculation rather than only the current s and p orbitals, the optimised 'int=ultrafine scf=conver=9' result can be refined to 'int=ultrafine scf=conver=9 extrabasis' and at the bottom of the file the following added.

(blank line) P 0 D 1 1.0 0.55 0.100D+01

(blank line)

The ultrafine extrabasis calculation for the cis isomer can be found here DOI:10042/to-3173 and for the trans isomer DOI:10042/to-3179 . These calculations took about 15 minutes to run each.

The images and energies produced from these calculations are compared below:

Fig.1.cis loose opt

Fig.2.cis Ultrafine opt

Fig.3.cis Ultrafine extrabasis opt

Fig.4 trans loose opt

Fig.5.trans Ultrafine opt

FIg.6 trans Ultra fine extrabasis

You can see that for both cis and trans the medium level accuracy calculations (loose and ultrafine)dont draw in the bonds for the Mo-P and P-Cl bonds. This again is due to the distance that Gaussview classifies as being a bond. Obviously the atoms aren't close enough together for gaussview to consider a bond present, but this does not mean there isn't. The molecule has still been optimised and when running frequency calculations still vibrates (see later). The bond lengths for these three calculations are shown below for the bonds of interest:

Reduction in bond lengths as optimisation accuracy is increased

'	Cis Optimisation	'	'	Trans Optimisation	'	'
	Loose	Ultra	Extra P dAO	Loose	Ultra	Extra P dAO
P-Mo	2.52	2.52	2.47	2.48	2.45	2.42
P-Cl	2.40	2.24	2.12	2.40	2.24	2.12

This clearly shows that including the P dAO's inproves the accuracy of the calculation and reduces the bond lengths to a length within guassviews parameters. Now comparing the energy outcomes of the optimisation fo all three methods:

Comparison of cis and trans optimisation data

'	Cis Optimisation	'	'	Trans Optimisation	'	'
	Loose	Ultra	Extra P dAO	Loose	Ultra	Extra P dAO
Charge	0	0	0	0	0	0
Spin	singlet	singlet	singlet	singlet	singlet	singlet
Energy/a.u	-617.53	-623.58	-623.69	-617.52	-623.58	-623.69
Energy/KJ/mol	-1621311.89	-1637201.15	-1637504.92	-1621298.76	-1637198.53	-1637508.60
RMS/10^5a.u	8.775	1.687	3.011	6.170	1.333	2.422
Dipole/D	8.4778	1.2216	0.1915	0	0	0
Point group	C1	C1	C1	C1	C1	C1

Note that the energy in Hartrees (or atomic units) has been converted to KJ/mol using the conversion factor: 1 H = 2625.5 KJ/mol. Furthermore, the values used in the table are accurate to 2.d.p.

The transition from the loose calculation to the ultrafine calculation has the most significant difference on the total energy, reducing it by ~15900 KJ/mol for both isomers. This difference is then much smaller for the ultrafine to extrabasis set calculation being only ~300KJ/mol. Strictly speaking, these values are actually incomparable due to the different basis sets used, but it is possible to see the energies have been lowered. The values that are comparable are those using the same basis set across the two isomers; therefore it is is possible to see which conformer is the most thermally stable. From the final Extra PdAO calculation, it appears the trans conformation is more stable by 3.7KJ/mol. This is likely to be due to the balance between electronic and steric effects as well as environmental factors which can be looked at in more detail by analysing the geometry.

Geometry Comparison

Using the ultrafine extrabasis out files for both isomers, the bond lengths and angles can be measured and compared against each other as well as with literature values.

Comparison of cis and trans geometry data with literature

'	Cis	'	Trans	'
	Gaussian	Literature	Gaussian	Literature
Mo-P/A	2.47	2.58	2.42	2.50
Mo-C/A	2.02	1.97/2.06	2.06	2.01
C=O/A	1.17	1.16	1.17	1.16
P-Cl/A	2.12	-	2.12	-
P-Mo-P/degrees	96.13	94.78	180	180
C-Mo-C /degrees	89.82/178.49	83	180/180	180/180
C-Mo-P/degrees	90.72/173.8	91.7/173.2	180/91.64	180/87
Cl-P-Mo/degrees	115.33	-	119.41	-

Note: Literature values are for Mo(CO)4(PPh3)2

The Mo-P literature values are slightly longer than the ones generated here due to the increased steric bulky of the PPh3 groups preventing the P getting close to the metal. The reverse case is observed in the Mo-C bond length for the same arguement that the carbonyl ligands are smaller and can get closer to the metal center; carbonyl can get closer in the literature compound since the bulky ligands are pushed further away. This difference is more sigificant in the cis conformer since the bulky steric groups hinder each other more, lengthening Mo-P and shortening Mo-C. The C=O bond length remains unchanged in both molecules but is slightly longer than the literature value, potentially due to error in the calculation. Now comparing the angles, these comply nicely with literature for the trans, but are a little less accurate for the C-Mo-C bond on the cis. this, again will be linked to the difference in the molecules as well as error in the calculation.

Comparing the cis with the trans; You can see the Mo-C bond is shorter for the cis conformation compared to the trans. This is likely to be due to the ability of the C=O ligand to backbond to the metal center. Since the cis conformation has a dipole pulling the electron density away from the metal center and towards the electron withdrawing PCl3 groups, this will increase the likelyhood of pi backbonding from the carbonyl ligand compared to the symmetric trans state. This acts to shorten the Mo-C bond and make the C=O ligand more susceptible to attack. This also reflects the lengthening of the Mo-P bond, as it is pulled further from the metal center. Furthermore, the bond angle between the P-Mo-P is much smaller than the trans conformer, adding slight steric strain to the structure. This will make the cis conformer more reactive and hence less thermodynamically stable.

As already mentioned, the trans conformation is slightly more stable than the cis. If you wanted to reverse the stablity and favour the cis conformation, then changing R group on the PR3 ligand is the way forward. The stability of the complexes is a balance between electronic and steric effects. Therefore decreasing the electronwithdrawing nature of the R groups so there is more electron density around the metal centre will aid the cis conformer. Furthermore, reducing steric bulk that favours the trans conformation also favours cis. Therefore exchanging R=Cl to R=Me should help.

IR Vibrational Analysis

The Ultrafine (nonextrabasis) files were used to run the frequency calculations.

The IR frequency calculations can be found here for the cis isomer DOI:10042/to-3064 and for the trans isomer DOI:10042/to-3065 . These calculations took about 15 minutes to run each.

As stated early, the file should only converge to its full minimum when all the frequencies obtained in the frequency calculation are positive. However, as also stated earlier there are errors in Gaussview particularly when running calculations involving heavier atoms. This is proven by the one negative result seen at the beginning of both the cis and trans spectra. One negative result means that a transition state has been reached and hence we may not be in at the gobal minimum but stuck in a very close local minimum. None the less, the spectra data for these low frequency values is shown below.

cis and trans low frequency data

'	Cis	'	'	Trans	'	'
Vibrational mode	Vibrational image	Freq/cm-1	Intensity	Vibrational image	Freq/cm-1	Intensity
1		-5	0.0082		-2	0.036
2		24	0.0091		4	0

Since these values are at a low freqency, this means the bonds causing them are quite weak and the energy of the bonds must be very low. Therefore, at room temperature the molecules must exist in an excited state rather than the ground state. Furthermore, the negative value suggests we may be stuck in a transition state between the molecules. Why might this be? The energy at room temperature is RT=2.5KJ/mol. The difference between the cis and trans conformers is 3.7KJ/mol. Since there is error in the calculations, the true difference could actually be lower, and if it is <2.5KJ/mol, this allows the interconversion between the conformers and hence an equilibrium.

The main point of interest here is the change in vibrational frequencies of the C=O bond as we convert between cis and trans. Therefore analysing these vibrations:

cis and trans C=O vibrations data

'	Cis	'	'	'	Trans	'	'	'
Vibrational mode	Vibration image	Freq/cm-1	Intensity	Literature	Vibration image	Freq/cm-1	Intensity	Literature
42		1945	767	1893		1950	1476	1902
43		1949	1489	1908		1951	1463	1902
44		1958	650	1926		1977	0	-
45		2024	567	2020		2031	0	-

It appears there are 4 C=O stretching frequencies for both the cis and trans conformers. However, two of the trans vibrations (44 and 45) cancel each other out due to the high symmetry of the molecule. Furthermore, the trans vibrations 42 and 43 occur at very close frequencies and very similar intensities. The cis isomer has 4, close, but different vibrational frequencies. Therefore, in relation to the C=O region of the spectrum, 4 peaks should appear in the cis and only 1 in the trans. Lets look at the IR speactra to confirm.

cis isomer

trans isomer

Comparing the peaks around 2000cm-1, there two distinct peaks in the cis (one is broad so the signals are overlapping) and one in the trans. This consolidates the data. The literature values agree with this but are for the complex Mo(CO)4(PPH3)2 and hence are slightly off.

Mini Project: Electronic and Structure Analysis of Benzene v's Borazine and their Derivatives

Fig.1. the 7 molecules under investigation

Borazine is the inorganice version of benzene; it is an aromatic, 6 membered ring of HN=B(H)-NH bonds, rather than the former HC=C(H)-CH. Its reactivity has been studied in great deal, and it is well known that the two rings reaction differently. Benzene is far more resilient to attack whereas borazine is much more susceptible; borazine easily undergoes nucleophilic addition, whereas benzene, not so easily, undergoes substitution. For example the reactivity with HCl and elemental Bromine is different:

Borazine reactivity v's benzene reactivity

The difference in reactivity is linked to the electronic nature of the atoms making up the molecules. Therefore, substituting groups onto benzene and borazine will also alter the reactivity depending on the the electronic nature the groups attached; electron withdrawing groups (EWG) or electron donating groups (EDG). Also, the exchange of a heavier atom into the ring, i.e. substituting the Boron for a Phosporus may also change the molecular properties.

Aim: To investigate the differences in electronic properties and atomic structure of the following 7 molecules, in hope to explain differences in reactivity and molecular stability. This will be acheived by making comparisons on the following Gaussian calculations:

• Overall optimised energy of the molecule
• Dipole
• Geometric properties
• Molecular Orbitals
• Natural Bond Orbitals (NBO)
• Frequency analysis

Optimisation

Before any analysis can be done all the molecules need to be optimised. First this was done on a B3LYP/3-21G low accuracy basis set to get an initial optimisation, then a more accurate B3LYP/LANL2DZ was run. This second optimisation also contained the additional keywords 'int=ultrafine scf=conver=9 extrabasis' to be more accurate and include all the relevant orbitals. It is necessary to run all the calculations at this level due to molecule 7 containing the heavier, hypervalent atom, phosphorus. All calculations must be run at the same basis set in order to be able to compare the outcomes. Once optimised, the out files can be used to run IR analysis and confirm optimisation hit the global minimum.

First to be compared is benzene and borazine.

Benzene v's Borazine

I predict benzene will be lower in energy than borazine and have less IR peaks visible due to its symmetrical nature. I think the LUMO regions will be predominantly made up of p-orbitals due to the pi orbital, delocalised nature of the ring. Furthermore, i predict borazine to have an unequal distribution of charges around the ring due to the difference in electrongeativity and atomic weight of the atoms that make up the ring. I expect the unoccupied orbitals of boron to bare a higher coefficient than nitrogen to explain the ability to accept electron density.

The Optimisations were run and the out files for these are at the following links: Benzene DOI:10042/to-3215 and borazine DOI:10042/to-3216 . Both these calculations took ~1 minute to run.

To verify that these are the global minimum, the IR frequency calculation was run with the same basis set. The link for these files are: Benzene DOI:10042/to-3217 and for borazine DOI:10042/to-3219 These took no more than 2 minutes to run. The resulting spectra are shown below with a table of the frequencies and vibrations.

IR vibrations of Benzene and Borazine

'	'	Frequency/cm-1'	'	'
Vibration	Image	Benzene	Image	Borazine
1		697		430
2		1068		643
3		1068		648
4		1540		961
5		1540		1478
6		3212		1478
7		3212		2702
8	-	-		2702
9	-	-		3723
10	-	-		3723

benzene IR spectrum

borazine IR spectrum

Since all frequencies are positive the minimum has been reached and now the energies can be compared. A summary of the optimisation is shown in the table below:

Data following Ultrafine LANL2DZ Optimisation

'	Benzene	Borazine
Charge	0	0
Spin	singlet	singlet
Energy/a.u	-232.2133	-242.6540
RMS/a.u	0.00001024	0.00507
Dipole/D	0	0
Point group	C1	C1

The difference in energy between the two is 10.44a.u, or 27412KJ/mol. This is quite a large difference and is obviously considerable enough to cause a change in reactivity. Another factor that will affect reactivity is the dipole; it appears there is an overall dipole of zero for both molecules but alas! this does not mean their charge distributions are the same and hence has an important role indeciding molecular structure and electronic properties (see Later)! Notice how the point groups assigned are C1, this is actually incorrect as benzene is D6h and borazine is D3h. This is an error in gaussviews calculation and means a larger basis set and more accurate calculation would need to be run. However, for my comparisons, the current level of accuracy is good so i shall continue.

Also notice the difference in the IR spectra; there is an increase in spectral lines seen on the Borazine molecule compared to benzene. Although both molecules are similarly symmetric, there are increased vibrations viewed in borazine due to the different atoms making up the ring. Borazine has 10 stretches whereas Benzene only has 7. Only 4 appear in the spectra since there are 3 degenerate pairs of stretches and one non-degenerate one. In borazine, there are also 3 pairs, plus 4 non-degenerate ones, two of these being very close; overall there are 6 lines in the spectrum. You can see this in the images in the vibrations table. The degenerate stretches have the same dipole vectors pulling then in the same way.

Before the charge distrubution can be observed, an MO calculation must be run selecting 'full NBO'. Therefore, the next step is to run this Molecular Orbital (MO) calculation to see how the electron density varies between the molecules. Since a check point file couldnt not be generated from ultrafine optimised file, nor could one be generated from running a 6-31Gd calculation (a method to generate a checkpoint file when one will not appear due to errors in gaussview), the simplist 3-21G file will have to be used to generate the MO images. Now comparing the Natural bonding orbitals (NBO):

charge distribution across benzene

charge distribution across borazine

Note that the parameters were set to -0.3 to 0.3 to enable comparison across all the NBO analysis (this accounts for all the later comparisons also). The red shades are the negatively charged atoms, the black neutral and the green positively charged. The actual values that represent the ratio of the overall charge of the molecule that that atom is contributing relative to the elemental charge are also displayed on the images. This shows how the carbons on in the benzene ring are all equally charged and slightly negative and the hydrogens are slightly positive. Overall, there is not large dipole across the molecule. In contrast, borazines charge distribution alternates around the ring; the nitrogens are delta negative whereas the borons are delta positive. The hydrogens on nitrogen are also delta positive but those on the boron are about neutral. This is due to the nitrogen having a higher electronegativity drawing the electrons closer to it compared to boron. So lets see how this affects reactivity and is observed in the MO's; the MO's of interest are shown below:

benzene:HOMO-4

benzene:HOMO-1

benzene:HOMO

benzene:LUMO

benzene:LUMO+1

borazine:HOMO-4

borazine:HOMO-1

borazine:HOMO

borazine:LUMO

borazine:LUMO+1

The out files for tese calculations can be found at: benzene DOI:10042/to-3226 and borazine DOI:10042/to-3227 .

These show how the change in atoms in the ring affect the contribution each atom has to the bonding and antibonding orbitals. Since borazine and benzene are isoelectonic, the orbitals contain the same number of electrons and the orbitals are comparable. You can see that all benzene's bonding and antibonding orbitals are perfectly symmetric with all the MO's having the same weighing coefficient (because all the atoms within the ring are the same). The MOs of carbon are sp2 hybridised and hence the remaining unhybridised p orbital lie perpendicular to the ring. The orbitals overlap making up the delocalised pi system of 6 electrons (one from each carbon) shown in HOMO-4; since there are 6 delocalised electrons, the ring is considered as huckel aromatic (abides 4n+2). Borazine is also aromatic but to a lesser extend due to the difference in electronegativity of the boron and nitrogen making up the ring. The difference in electronegatively is 1.06 Pauling units, where nitrogen is more electronegative and lying deeper in energy than boron. This difference in electronegativity means the bonding and antibonding orbitals are dominated by nitrogen and boron respectively. You can see the LUMO has large diffuse orbitals on the borons, making them susceptible to nucleophilic attack. Again, these are p ortibals lying perpendicular to the ring and account for the lewis acidiity of the boron atom, being susceptible to nucleophilic attack; the nitrogens are more susceptible to electrophilic attack. This aromaticity is all seen, and can be compared, in the NBO second order pertubation of the log files.

benzene pertubation of NBO

borazine pertubation of NBO

The values of E(2) here are above 20 and hence take some interesting significance. They refer to the amount of donation from one bonding orbital in the molecule to another. THe left column is the donar and the right the acceptor. The files show that there are 6 donations/acceptances from the benzene C-C pi bonds to the benzene C-C pi* bonds. In borazine, there are only 3. Therefore, although the E(2) value is higher for the borazine, there is only half the amount, reducing the aromaticity of the ring. This is depicted below:

benzene delocalisation from pertubation results

borazine delocalisation from pertubation results

Furthermore, the energy difference between the HOMO and the LUMO of benzene and borazine should be considerably different according to literature, accounting for the ability to undergo additions and loose aromaticity rather than substitutions and retain aromaticity like benzene (see MO diagram below). Unfortunately, according to my calculations (see below images), both HOMO and LUMO gaps are the same (at 0.246a.u = 6.7eV). This error must be related to the low accuracy of the calculation since the 3-21G basis set optimisation was used here to generate the orbital diagrams. The energy levels do however highlight the lower energy of benzenes LUMO compared to Borazine; Benzene LUMO = 0.005 a.u. whereas borazine = 0.028ac.u.

Borazine MO energies

Benzene MO energies

Comparison of benzene (D6h) and borazine (D3h) MO diagrams

All in all, this helps to explain the increased reactivity of borazine over benzene and how its reduced aromaticity and higher energy LUMO allows it to react more readily.

Now we must consdier what would happen if we add other substituents to the rings or change another atom in the ring; what affect would a chlorine atom have? or a Me group? or changing a Boron in the ring to a Phosporus? The following questions will be examined. I predict the chlorine atom, being electron withdrawing, will reduce the electron density in the ring and hence reduce the aromaticity of the rings. In contrast, the me group is electron donating so could act to stabilise the ring, and if donation occurs into the ring, may reduce reactivity. I predict if donation does occur, there will be more on when substituted on the Boron than Nitrogen since this is more electro positive with a larger antibonding orbital ready to accept electrons. Finally, the change from boron to phosporus may reduce aromaticity due to the larger, more diffuse, accessible d orbitals present to accept and donate electrons. I also predict the homo-lumo region to be much higher in energy for the PN ring than the others due to reduced electronegativity and larger AO's. Now lets see...

Adding EWG and EDG to the rings and exhange for heavier atoms

Now molecules 3 to 7 will be considered. Firstly, optimisation was carried out the same as molecule 1 and 2 (3-21G followed by LANL2DZ).

OPtimised out file for trichlorobenzene (3) can be found here: DOI:10042/to-3231

OPtimised out file for B-sub-Chloroborazine (4) can be found here: DOI:10042/to-3232

OPtimised out file for B-sub_Methylborazine (5) can be found here: DOI:10042/to-3233

OPtimised out file for N-sub_Methylborazine (6) can be found here: DOI:10042/to-3234

OPtimised out file for Chlorophosphazene (7) can be found here: DOI:10042/to-3336

Again, the IR spectra were run to make sure the molecule has been optimised to the global minimum:

Frequency out file for trichlorobenzene (3) can be found here: DOI:10042/to-3235

Frequency out file for B-sub-Chloroborazine (4) can be found here: DOI:10042/to-3236

Frequency out file for B-sub_Methylborazine (5) can be found here: DOI:10042/to-3237

Frequency out file for N-sub_Methylborazine (6) can be found here: DOI:10042/to-3238

Frequency out file for Chlorophosphazene (7) can be found here: DOI:10042/to-3337

MO calculations were also run as before and information from these ie. MO images, will be used throughout the following section.

MO out file for (3) can be found here: DOI:10042/to-3399

MO out file for (4) can be found here: DOI:10042/to-3400

MO out file for (5) can be found here: DOI:10042/to-3402

MO out file for (6) can be found here: DOI:10042/to-3403

MO out file for (7) can be found here: DOI:10042/to-3405

All the files converges and reached a minimum so can now be compared with Benzene and Borazine:

Data following Ultrafine LANL2DZ Optimisation

'	Benzene(1)	Borazine(2)	TCB(3)	BsubClBorazine(4)	BsubMeborazine(5)	NsubMeBorazine(6)	Chlorophosphazene(7)
Charge	0	0	0	0	0	0	0
Spin	singlet	singlet	singlet	singlet	singlet	Singlet	doublet
Energy/a.u	-232.2133	-242.654	-275.2191	-285.8318	-360.6312	-360.5368	-275.3734
RMS/a.u	0.00001024	0.00507	0.005577	0.0001606	0.001367	0.00001519	0.00008276
Dipole/D	0	0	0.0006	0.0001	0.00445	0.0005	0.3309

The change in energy from benzene to trichlorobenzene is same as the change in energy from borazine to B-sub-chloroborazine at 43 a.u. Now adding the Chlorine atoms to the nitrogen instead, has a much larger effect, similar to that of adding the methyl group to the borons, the difference here being 117.88a.u. and 119.97a.u. respectively. The difference in energy between B-N ring and P-N ring is much less significant, being 10.5a.u. between molecule 7 and molecule 4. Again, here the dipoles are going to affect reactivity. Instead of not having one, this time, the dipole increases as substiutents are added, likely to make the molecule more reactive. Highlighting the distribution of charge pictorially again (red=negative, black=neutral,green=positive) helps to visualise the distribution over the molecules:

1. benzene

2. Trichlorobenzene(TCB)

Immediately you can see how the addition of the chlorine atoms reduces the electron rich nature of the C-C ring, rendering each alternate C carbon. However, it is interesting to note how the electronegative chlorine atoms are not holding a red negative charge. This must mean the C atoms would rather donate electrons into the ring and retain stability than donate them to the chlorine. This can be shown in the NBO perturbation analysis section of the log file as before, and by viewing the bonding MOs. Notice how the E(2) value is slightly lower but virtually the same and the MO's are still circulating around the whole of the ring. This means the addition of the chlorine atoms doesnt significantly affect the aromaticity of the ring.

2.TCB: donation maintained in ring system

TCB: HOMO-2

TCB: HOMO

TCB:LUMO

Notice how the lumo is perfectly symmetric like that of benzene but has more nodes so probably lies higher in energy than the benzene lumo; these two opposing factors, symmetry and depth of lumo energy level, will affect the reactivity of trichlorobenzene, probably acting to retain it at a similar level to benzene.

3. Borazine

4. B-sub-Cl-Borazine

5. B-sub-Me-Borazine

6.N-sub-Me-Borazine

In contrast to the neutral nature of the TCB chlorines, the chlorines in the B-sub-chloroborazine do retain their negative charge and the borons are now slightly more positive compared to the borazine alone. This will be due to the higher electronegativity difference between boron and chlorine compared with carbon and chlorine. The nitrogens here become slightly more negative. Comparing this with molecule 5, that is methyl groups rather than Cl's, the boron has now become even more positive, and the Methyl Carbon is more negative than the Cl. This is unusual since you would expect the chlorine to be more negative. Now changing the methyl groups to the N position as in molecule 6, you can see the charges on the B's and N's have reversed back to that like in the orginal borazine; the boron is now positive and the nitrogen now negative. The Nitrogen is more negative than the carbon on the Methyl group reflecting nitrogens electronegativity. Again, by analysising the files to see how this has affected aromaticity:

• molecule 4: donation from the B=N pi orbital to another B=N pi* orbital as in borazine, has increased from E(2)=34 to E(2)=38
• molecule 5: the same donation: E(2) has increased to 37
• molecule 6: the same donation E(2) has decreased to 34

This shows, that the addition of a usually EWG, and an EDG has increased aromaticity when attached to the boron (since they can donate electrons into the large, diffuse, lumo) but left aromaticity unaffected when attached to the Nitrogen. This should act to stabilise molecules 4 and 5 compared to borazine, rendering them less reactive, but not so much on molecule 6. The reactivity of 6 is also likely to be the same as borazine in the boron positions since the boron empty orbitals are still open to attack. The only thing that may reduce the reactivity is if the me groups are exchanged for more bulky alkyl ligands so there is a physical barrier in the way.

7. Chloro phoshpazene

Finally, comparing the exchange of a boron to a phosphorus atom within the ring, maintains a similar charge distribution to molecule 4, B-sub-Clborazine; the nitrogens are negative, though slightly more negative here, and the P positive, also slightly more positive. The Cl atoms are about the same. Looking at the pertubation here, all the E(2) values are below 20, suggesting no aromaticity. However, there are some values nearer to 20 that could be of some significance.

molecule 7: NBO pertubation

These show that there is a significant amount of donation from the nitrogen sigma LP into the P-Cl sigma* orbital, occuring 4 times around the ring but there is no real aromaticity. This is shown in the MO diagrams as well; comparing the LUMOs of the substituted molecules:

7. lumo

4. Lumo

5. Lumo

6. Lumo

You can see how the chlorophosporine (7), has much larger diffuse orbitals on the chlorine atoms compare with 4 where the density is more spread over the entire molecule. Molecules 5 and 6, the methyl substituted ones, have more electron density on the rings rather than the substituents, highlighting their electon donating nature. One other thing that will affect the reactivity is the HOMO/LUMO levels as well as the HOMO-LUMO gaps.

HOMO LUMO energies and gaps of molecules 1-7

'	1.Benzene	2.TCB	3.Borazine	4.BsubCl Borazine	5.BsubMe Borazine	6.NsubMe Borazine	7.Cl Phosphazene
HOMO	-0.251	-0.281	-0.274	-0.307	-0.253	-0.247	-0.28
LUMO	0.005	-0.0471	0.027	-0.007	0.049	0.025	-0.25
HOMO-LUMO gap	0.256	0.233	0.30	0.30	0.302	0.272	0.03

This shows how all the HOMOS are of similar energy but the LUMOS are different. Molecules 2, 4, and 7 have very low lying negative energy orbitals and hence are actually non-bonding orbitals rather than antibonding orbitals. The fact that these lie deeper in energy, reduces their reactivity. However, since they lie deeper in energy, they are closer to the HOMO, reducing the HOMO-LUMO gap, actually leading to increased reactivity; orbitals of the same symmetry will be able to excite electrons and ultimately raise the energy of the molecule allowing reactivity (photochemistry). The smallest HOMO-LUMO gap is in molecule 7, all the others are relatively similar so wont tell us much about the difference in reactivity when comparing these particular molecules.

One other factor that can be compared, is the geometries of the molecules:

Benzene v's Trichlorobenzene Bond Lengths

Bond lengths /A	Benzene	TCB
C-C	1.41	1.4
C-H	1.09	1.08
C-Cl		1.81

Borazine v's borazine derivatives Bond Lengths

Bond lengths /A	Borazine	BsubCl Borazine	BsubMe Borazine	NsubMe Borazine
B-N	1.44	1.43	1.44	1.44
B-H	1.19			1.19
N-H	1.01	1.01	1.01
B-Cl		1.82
B-Cl			1.59
N-C				1.48

Phosphazene Bond Lengths/Å

'	Cl Phosphazene
N-H	1.02
N-P	1.69
P-Cl	2.30

Again this highlights the aromaticity; the average C-C bond length 1.54Å and the average C=C bond length is 1.34Å.. Since the benzene C-C bond lengths are a hybrid of these two lengths, this shows they are between a single and a double bond. This is similar for the borazine, but the bond is alot longer for the phosphazene, highlighting the lack of aromaticity; the P-N bond is even longer than the C-C single bond, rendering it alot weaker. On the contrary, literature values say the P-N single bond is 1.77Å and the P=N bond is 1.58Å; since my value lies between this, this suggests some aromaticity may be present. Overall, the phosphazene would be more reactive due to the increased bond lengths. Furthermore, you can see that all the bond lengths are virtually unchanged when moving through this series of molecules, highlighting the stability of the rings.

Although, this doesnt share much information about the stability of the molecules, one final comparison can be made on the shifts in the IR spectra of the borazine derivative series.

3. borazine IR spectrum

4. BsubClBorazine

5. BsubMeBorazine

6. NsubMeBorazine

You can see, the B-H stretch at ~2500cm-1 is lost as you move from 3 to 4 as the hydrogen is exchanged for a Cl atom. Furthermore, some of the lower stretches are also lost, likely to be linked to B-H stretches also. Exchanging the Cl's for Me's, loses the B-Cl stretch and gains B-Me stretch around 1000cm-1. Now moving the methyl groups onto the N atom, leads to increased stretches around 1500cm-1, 2600, and 3100cm-1. this will naturally be linked to the N-Me bond. The higher frequency nature of the N-Me vibrations suggests this bond is stronger than the B-Cl and B-Me bonds.

Conclusion

Overall, the stabilities of the molecules were compared and reasons behind their reactivity considered. As predicted, benzene is more stable and aromatic that borazine due to its symmetrical structure and electron distribution. This has been shown by comparing the charge distribution, MO's, pertubations of the NBO analysis, and HOMO-LUMO gaps. Addition of substituents to benzene (namely chlorine) doesnt seem to have much of an effect on its reactivity but addition to borazine may have; the extra atoms increase aromaticity when groups are attached to Boron, but is left unaffected when attached to nitrogen. This may act to decrease reactivity. The exchange of the B for P in the ring, leads to considerable reduced aromaticity, but in exchange, some extra donation from the nitrogen LP to the P-Cl bond. This may act to increase reactivity about the P-Cl bond. The geometries of the molecules appear unaffected to the degree of accuracy that the calculations are to.

There are some limitations and systematic errors in the calculations due to gaussview. Since i was unable to generate a checkpoint file from the more accurate calculations (LANL2DZ) it was necessary to gain my MO data from a lower level (3-21G) basis set level. This meant that any information gained from these files may not be to a high enough level of accuracy as they could be. None the less, the images still highlight the main points needed to observe the differences between the molecules.

I think this project was a success and i have found out some interesting points about the aromaticity of the molecules considered and how their reactivities may be affected as a result.