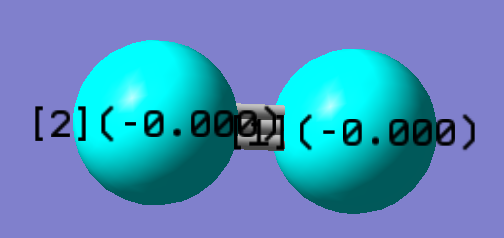Mod-Xxn
NH3 Optimisation
test molecule |
The optimisation file is linked to here
Calculation Method
calculation method = RB3LYP
Basis Set
basis set = 6-31G(d,p)
Final Energy E(RB3LYP)in Atomic Units (au)?
E(RB3LYP) = -56.55776873 a.u.
Point Group
point group = C3v
Item
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000004 | 0.000450 | YES |
| RMS Force | 0.000004 | 0.000300 | YES |
| Maximum Displacement | 0.000072 | 0.001800 | YES |
| RMS Displacement | 0.000035 | 0.001200 | YES |
Bond length and angle
NH3 is in trigonal pyramidal shape. The N-H bond length is 1.01798 and the H-N-H bond angle is 105.74115 degrees.
Vibrations of the molecule
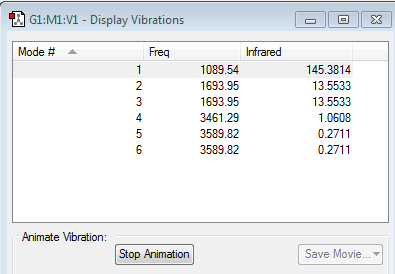
From the 3N-6 rule, six vibrational modes are expected since N=4,thus,3N-6=6.
As shown in the image above, there are six modes in total, which is the same as we expected. Mode 2&3 are degenerate and have frequency equal to 1693.95. Furthermore, mode 5&6 are degenerate as well and have frequency 3589.82.
Among all the vibrational modes, the first three modes are "bending" vibrations while the 4,5 and 6 modes are "bond stretch2 vibrations. Mode1 is known as the umbrella mode and \mode4 is highly symmetric. since there are four different enegies, four bands are expected to see in an experimental spectrum of gaseous ammonia.
Charge on the molecule
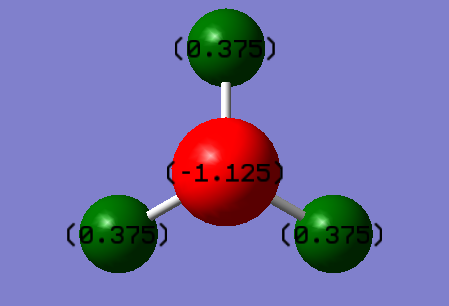
The Nitrogen atom is expected to be partial negative since nitrogen is more electronegative than hydrogen and will attract the electrons in the hydrogen atom towards itself. The hydrogen atom is expected to be partial positive because the electrons are attracted by nitrogen and move away.
As shown in the picture above, the red atom is nitrogen ad has charge of -1.125. The green atoms are hydrogen atoms, they have equal charge of +0.375
H2 Optimisation
test molecule |
The optimisation file is liNked to here
Calculation Method
calculation method = RB3LYP
Basis Set
basis set = 6-31G(d,p)
Final Energy E(RB3LYP)in Atomic Units (au)?
E(RB3LYP) = -1.15928020 a.u.
Point Group
point group = D*H
Item
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000000 | 0.000450 | YES |
| RMS Force | 0.000000 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000001 | 0.001200 | YES |
Vibrations of the molecule
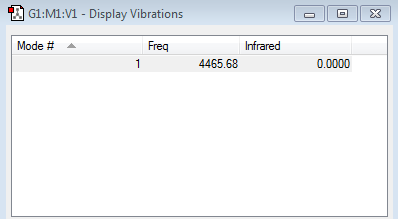
There is only one vibration mode for hydrogen gas molecule. However, if we are going to follow the 3N-6 rule, it should have no vibration mode. This is because the 3N-6 rule does not apply to diatomic molecules.
Also, this is a bond stretching vibration.
Charge on the molecule
Hydrogen gas molecule is a neutral molecule since it is made of two atoms with the same electronegativity. Thus, the electrons are evenly distributed around the molecule. The charge on both of the molecule is 0.
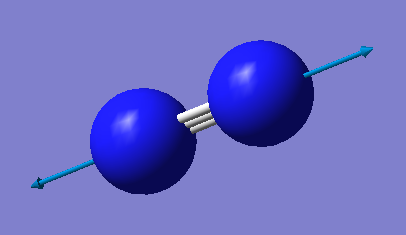
N2 Optimisation
test molecule |
The optimisation file is liNked to here
Calculation Method
calculation method = RB3LYP
Basis Set
basis set = 6-31G(d,p)
Final Energy E(RB3LYP)in Atomic Units (au)?
E(RB3LYP) = -109.52359111 a.u.
Point Group
point group = D*H
Item
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000001 | 0.000450 | YES |
| RMS Force | 0.000001 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000000 | 0.001200 | YES |
Vibrations of the molecule
There is only one vibration mode for nitrogen gas molecule, same as for hydrogen. The 3N-6 cannot be applied, since nitrogen gas molecule is a diatomic molecule.
Also, this is a bond stretching vibration.
Charge on the molecule
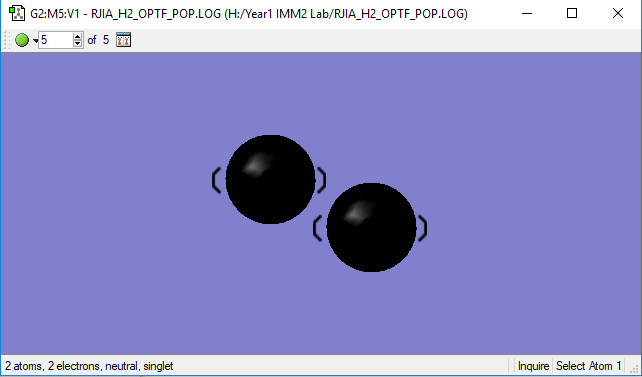
Nitrogen gas molecule is a neutral molecule since it is made of two atoms with the same electronegativity. Thus, the electrons are evenly distributed around the molecule. The charge on both of the molecule is 0, as shown on the image above.
Calculation of reaction energies
E(NH3)= -56.55776873 a.u. = -148492.422 kJ/mol
2*E(NH3)= -113.11553746 a.u. = -296984.844 kJ/mol
E(N2)= -109.52359111 a.u. = -287554.188 kJ/mol
E(H2)= -1.15928020 a.u. = -3043.611 kJ/mol
3*E(H2)= -3.4778406 a.u. = -9130.833 kJ/mol
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.11410575 a.u. = -299.585 kJ/mol
Thus, the energy taken to convert nitrogen gas and hydrogen gas to ammonia is -299.585 kJ/mol. Therefore, the ammonia product is more stable than the gaseous reactants since the product is of lower energy.
However, the literature value of the standard enthalpy of formation is -46.0kJ/mol. The huge difference might due to the errors when doing the calculation. Also, it might because the bond length of the optimised NH3 orbital is not the same as the actual NH3 orbital.
H2SiO Optimisation
test molecule |
The optimisation file is liNked to here
Calculation Method
calculation method = RB3LYP
Basis Set
basis set = 6-31G(d,p)
Final Energy E(RB3LYP)in Atomic Units (au)?
E(RB3LYP) = -365.90001403 a.u.
Point Group
point group = CS
Item
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000023 | 0.000450 | YES |
| RMS Force | 0.000009 | 0.000300 | YES |
| Maximum Displacement | 0.000022 | 0.001800 | YES |
| RMS Displacement | 0.000017 | 0.001200 | YES |
Vibrations of the molecule
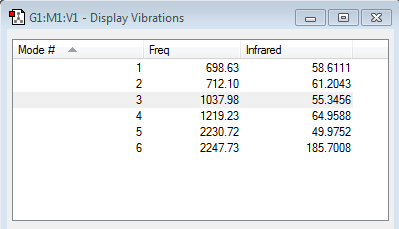
There are six vibration modes in total for H2SiO molecule in total, as shown in the image above. The number of modes fit the 3N-6 rule.
among all the vibration modes, the first three are "bent" vibration while the 4th, 5th and 6th ones are "bond stretching" vibrations. Non of the vibrations are degenerate, they all have different energies.
Charge on the molecule
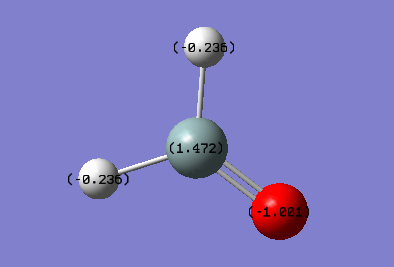
As shown in the picture, the central atom Si is partial positive and has charge +1.472, this is because the electrons are being attracted towards the Si-O double bond and the electronegative oxygen. The Oxygen atom is partial negative and has charge -1.001. The two hydrogen atoms are also partial negative since they are more electronegative than silicon atom. The two H atoms have charge -0.235.
Molecular orbitals
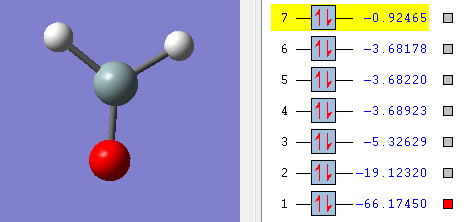
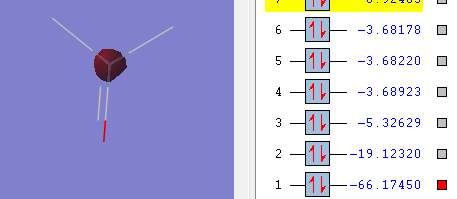
The above picture shows the 1s orbital for the central silicon orbital, this is a non-bonding orbital and the shape looks similar to s atomic orbital. The energy of the orbital is -66.1750 a.u.
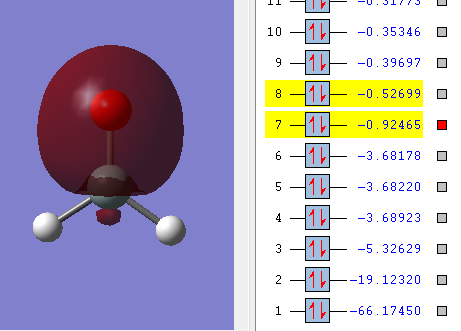
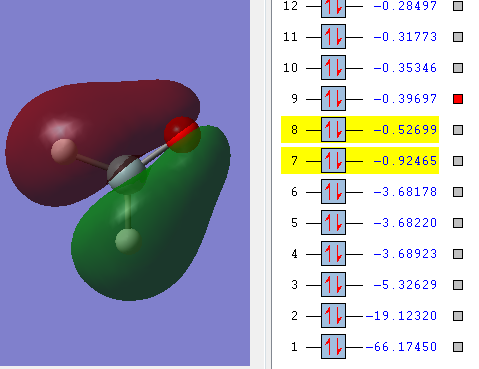
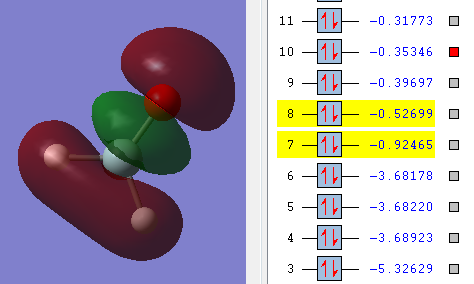
This is a bonding molecular orbital and it is made of the 2s orbital from oxygen and 3p orbital from silicon. The hydrogen atoms don't contribute to this molecular orbital. The energy of the orbital is -0.92465 a.u., the value is much higher than the non-bonding orbital.
This is also a bonding molecular orbital. The p orbitals in oxygen atom and silicon atom as well as 1s orbitals in two hydrogen atoms contribute in this molecular orbital. The energy is -0.39697.
This bonding molecular orbital is similar to the 9th molecular orbital above since the atomic orbitals contribute to it is also p orbital in oxygen atom and silicon atom as well as s orbitals in two hydrogen atoms. However, the p orbitals of oxygen and silicon are different from the ones in 9th molecular orbital, the direction is different, thus, the shape of the molecular orbital is different. The energy of this molecular orbital, which equals -0.35346 a.u., is also quite similar to the previous one.
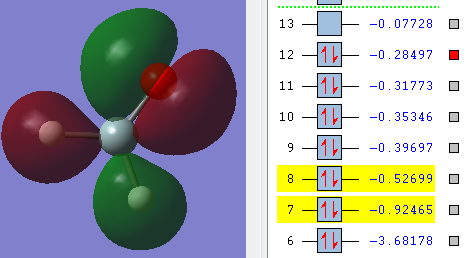
The last molecular orbital presented here is an anti-bonding molecular orbital, and it is the highest occupied molecular orbital(HOMO). 1s orbitals in two hydrogen atoms, 2p orbital in oxygen and 3p orbital in silicon atom contribute to the molecular orbital. The energy of this molecular orbital is the highest among all the occupies orbitals, the value is -0.28497 a.u.