Mod=tyy15
NH3
Summary
Calculation Method: B3LYP
The Basis Set: 6-31G(d,p)
Type of calculation to do: OPTF
Final energy E(RB3LYP): -56.55776873 a.u.
Point Group: C3V
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986326D-10
NH3 molecule |
The optimisation file is linked to here
Vibrations

How many modes do you expect from the 3N-6 rule?
We would expect 6 modes as N is 4 for NH3.
Which modes are degenerate (ie have the same energy)?
Mode 2 & 3 and Mode 5&6 since they have the same frequencies and same intensities.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Modes 1,2 &3 are the bending vibrations and Moed 4,5 & 6 are the Bond stretch vibrations.
Which mode is highly symmetric?
Mode 4
One mode is known as the "umbrella" mode, which one is this?
Mode 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
2 Bands are expected to be seen in an experimental spectrum of gaseous ammonia.
Charge Distribution
N-Atom : -1.125C
H-Atom : 0.375C
We would expect to see a negative charge on N as Nitrogen is electronegative. H would be positive as its electrons are being pulled to the nitrogen - making a partially positive charged.
N2
Summary
Calculation Method: B3LYP
The Basis Set: 6-31G(d,p)
Type of calculation to do: OPTF
Final energy E(RB3LYP): -109.52412868 a.u.
Point Group: D∞h
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000003 0.001200 YES Predicted change in Energy=-1.248809D-11
N2 molecule |
The optimisation file is linked to here
Vibrations

How many modes do you expect from the 3N-5 rule?
We would expect 1 mode as N is 2 for N2.
Which modes are degenerate (ie have the same energy)?
There is only 1 mode, ie no modes are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Mode 1 is the stretching frequency.
Which mode is highly symmetric?
Mode 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
0 since The mode in the table has no change in dipole moments.
Charge Distribution
N-Atom : 0.000C
N-Atom : 0.000C
We would expect to see a neutral charge on both of the nitrogens since their electroneagtivities are the same.
H2
Summary
Calculation Method: B3LYP
The Basis Set: 6-31G(d,p)
Type of calculation to do: OPTF
Final energy E(RB3LYP): -1.17853936 a.u.
Point Group: D∞h
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13
H2 molecule |
The optimisation file is linked to here
Vibrations

How many modes do you expect from the 3N-5 rule?
We would expect 1 mode as N is 2 for H2.
Which modes are degenerate (ie have the same energy)?
There is only 1 mode, ie no modes are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Mode 1 is the stretching frequency.
Which mode is highly symmetric?
Mode 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
0 since The mode in the table has no change in dipole moments.
Charge Distribution
H-Atom : 0.000C
H-Atom : 0.000C
We would expect to see a neutral charge on both of the hydrogens since their electroneagtivities are the same.
Haber-Bosch Reaction Energy Calculation
We can determine the energy for the reaction of N2 + 3H2 -> 2NH3.
E(NH3)=-56.55776873 a.u.
2*E(NH3)=-113.11553746 a.u.
E(N2)=-109.52412868 a.u.
E(H2)=-1.17853936 a.u.
3*E(H2)=-3.4778406 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.0557907 a.u.
Which equals = -146.4784828 kJ/mol
This means it takes -146.4784828 kJ/mol to convert nitrogen and hydrogen to ammonia. The ammonia product will be more stable since the reaction is exothermic and the product will be favored as its more stable.
The literature value for this reaction is -92.44 kJ/mol. [1]
- ↑ Max Appl "Ammonia" in Ullmann's Encyclopedia of Industrial Chemistry 2006 Wiley-VCH, Weinheim. doi:10.1002/14356007.a02_143.pub2
O2
Summary
Calculation Method: B3LYP
The Basis Set: 6-31G(d,p)
Type of calculation to do: OPTF
Final energy E(RB3LYP): -150.32004019 a.u.
Point Group: D∞h
Item Value Threshold Converged? Maximum Force 0.000114 0.000450 YES RMS Force 0.000114 0.000300 YES Maximum Displacement 0.000069 0.001800 YES RMS Displacement 0.000097 0.001200 YES Predicted change in Energy=-7.817742D-09
O2 molecule |
The optimisation file is linked to here
Vibrations
How many modes do you expect from the 3N-5 rule?
We would expect 1 mode as N is 2 for O2.
Which modes are degenerate (ie have the same energy)?
There is only 1 mode, ie no modes are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Mode 1 is the stretching frequency.
Which mode is highly symmetric?
Mode 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
0 since The mode in the table has no change in dipole moments.
Charge Distribution
O-Atom : 0.000C
O-Atom : 0.000C
We would expect to see a neutral charge on both of the oxygens since their electroneagtivities are the same.
Laboratory Preparation of Oxygen, Energy Calculation
The laboratory preparation of oxygen can be done through the decomposition of hydrogen peroxide.
The reaction equation is : :2 H2O2 → 2 H2O + O2
E(H2O2)=-151.47376849 a.u.
2*E(H2O2)= -302.947537 a.u.
E(O2)= -150.32004019 a.u.
E(H2O)=-76.18787037 a.u.
2*E(H2O)=-152.3757407 a.u.
ΔE=2*E(H2O2)-[E(O2)+2*E(H2O)]= -0.25175605 a.u.
Which equals = -660.9855093 kJ/mol
This can be compared to a literature value of 94.6 kJ/mol[1]
- ↑ Charles J. Marzzacco, The Enthalpy of Decomposition of Hydrogen Peroxide http://pubs.acs.org/doi/pdf/10.1021/ed076p1517
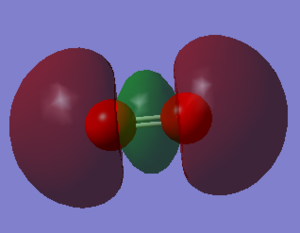
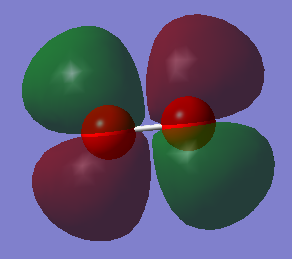
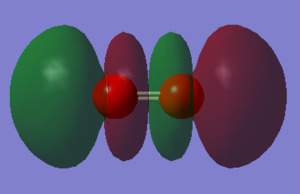
Molecular Orbitals
The Electron configuration of oxygen atom is 1s22s22s4
Atomic orbitals (AO) combine to form the molecular orbitals (MO).
The MO with the lowest energy is the 1s orbital. These MOs are -19.31 au much deeper than the Mos formed from the valence shell AOs. These AOs do not overlap and they are only held to their respective O atom.

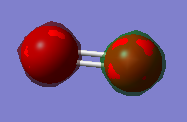
The other MOs will have different shapes and different interaction since they are formed by the different orbitals overlap. Two types of interaction are present in the O2 moecule: the sigma interaction along the bond and the pi interaction perpendicular to the bond.
The pAO will form low energy orbital, for example the 6th MO is the pi 2p MO and has a -0.55938 a.u. energy. Orbital 5 and 6 have the same energy (-0.55938) so they are said to be degenerate. When the bond is formed it forms the pi MO. The 7th orbital has the MO formed from the bonding overlap of the along bond pAOs due to 'mixing'. The 8th MO and the 9th MO are degenerate (-0.30818 a.u.) and they are the result of the antibonding combination of the perpendicular pAOs. They are the pi* 2p orbital. The 10th MO shows the antibonding MO of the bond along pAOs and its the sigma* 2p orbital. It has a high and positive energy (0.19634 a.u.). From the 5th MO to the 10th MO they are all from the 2p orbitals. The 8th and 9th MO are the HOMO and the 10th MO is the LUMO.