Mod=EW515
Energetic Analysis of Haber-Bosch Process
Currently one of the most important chemical reactions in the agricultural industry, the Haber-Bosch process is used to create ammonia from nitrogen gas, N2, and hydrogen gas, H2. Below, are the models, optimizations, and summary energy information for the reactants involved. Based on the information for NH3 above, the net energy for this reaction will be calculated.
NH3 Optimization
Ammonia Model |
Utilizing the program Gaussian, an ammonia molecule with a point group of C3v was modeled and then optimized. The optimization was carried out via the calculation method RB3LYP, with a basis set of 6-31G(d,p). The final energy, E(RB3LYP), for the optimized NH3 molecule was found to be -56.55776873 au.
The optimized force values and energy displacements calculated were found to be,
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986273D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The full .log Gaussian file can be found here.
Vibrational/Frequency Analysis
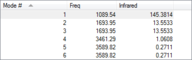
As a non-liner molecule, ammonia could be considered by the "3N-6" rule, which would suggest 6 different vibrational modes for the molecule (4 total atoms, N). Seen in the figure to the left, the pairs of modes 2/3 and 5/6 are of degenerate energies. The three lowest energy modes available to ammonia are bond "bending" vibrations, while the three higher level modes available are bond "stretching" vibrations. Below is a comparison between Modes 1, a bending vibrational mode, and mode 4, a stretching vibrational mode. Furthermore, mode 4 is seen to be a highly symmetric mode of the six available, while mode 1 is known as the "umbrella" mode. As the number of bands in an experimental IR spectrum depends on the number of discrete frequencies which act on the molecule, it could be expected that Ammonia would have four separate bands measured.
Atomic Charges
As can be seen in the image to the right, the largest region of electron density for the NH3 molecule
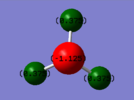
is centered on the Nitrogen atom, while the positive charge is dispersed degenerately over the three hydrogen atoms. This is in accordance with what would be expected from the observation that Nitrogen has a filled non-bonding p orbital centered around its nucleus and contributes more to the N-H sigma bonding orbitals due to its higher electronegativity.
H2 Optimization
H2 Model |
Utilizing the program Gaussian, an H2molecule with a point group of D∞h was modeled and then optimized. The optimization was carried out via the calculation method RB3LYP, with a basis set of 6-31G(d,p). The final energy, E(RB3LYP), for the optimized NH3 molecule was found to be -1.17853936 au.
The optimized force values and energy displacements calculated were found to be,
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The full .log Gaussian file can be found here.
Vibrational/Frequency Analysis

As a liner molecule, H2 could be considered by the "3N-5" rule, which would suggest 1 unique vibrational mode for the molecule (2 total atoms, N). The one mode available to H2 is a bond-stretching mode, as supported by its higher IR frequency and energy. As the number of bands in an experimental IR spectrum depends on the number of discrete frequencies which act on the molecule, it could be expected that H2 would only have one distinct band measured.

N2 Optimization
N2 Model |
Utilizing the program Gaussian, an N2 molecule with a point group of D∞h was modeled and then optimized. The optimization was carried out via the calculation method RB3LYP, with a basis set of 6-31G(d,p). The final energy, E(RB3LYP), for the optimized NH3 molecule was found to be -109.52412868 au.
The optimized force values and energy displacements calculated were found to be,
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400956D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The full .log Gaussian file can be found here.
Vibrational/Frequency Analysis

As a liner molecule, N2 could be considered by the "3N-5" rule, which would suggest 1 unique vibrational mode for the molecule (2 total atoms, N). The one mode available to N2 is a bond-stretching mode, as supported by its higher IR frequency and energy. As the number of bands in an experimental IR spectrum depends on the number of discrete frequencies which act on the molecule, it could be expected that N2 would only have one distinct band measured.
Net Energy for Reaction
- E(NH3)= -56.55776873 au
- 2*E(NH3)= -113.11553746 au
- E(N2)= -109.52412868 au
- E(H2)= -1.17853936 au
- 3*E(H2)= -3.53561808 au
- ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= (-113.11553746)-[(-109.52412868)+(-3.53561808)] = - 0.0557907 au (-146.47849401 kJ mol-1)
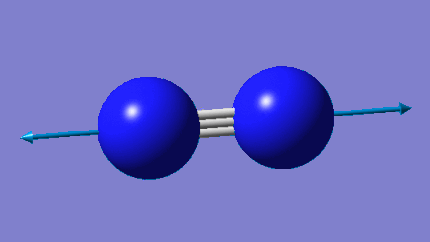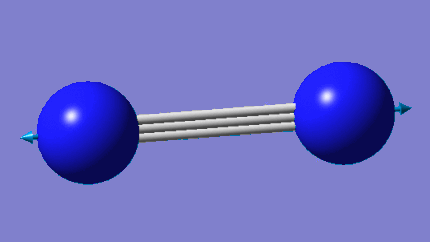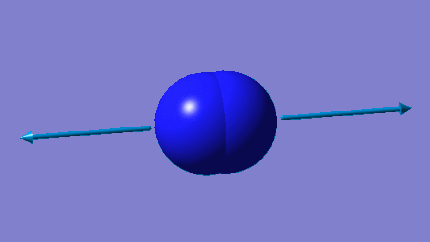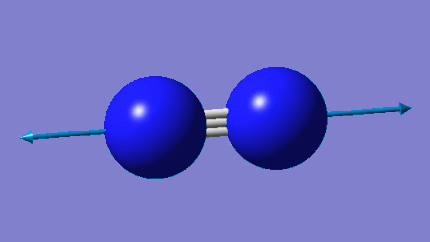
Cyanide Ion Optimization
Cyanide Model |
Utilizing the program Gaussian, a cyanide molecule (CN-) with a point group of C1 was modeled and then optimized. The optimization was carried out via the calculation method RB3LYP, with a basis set of 6-31G(d,p). The final energy, E(RB3LYP), for the optimized NH3 molecule was found to be -92.82453153 au.
The optimized force values and energy displacements calculated were found to be,
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-6.650387D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1841 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The full .log Gaussian file can be found here.

Vibrational/Frequency Analysis
As a linear molecule, EtOH could be considered by the "3N-5" rule, which would suggest 1 unique vibrational mode for the molecule (2 total atoms, N). Seen in the figure to the left, cyanide has exactly one vibrational mode available to it, a simple bond stretch. As the number of bands in an experimental IR spectrum depends on the number of discrete frequencies which act on the molecule, it could be expected that cyanide would have only one distinct band measured.
Atomic Charges

As can be seen in the image to the right, the largest region of electron density for the cyanide molecule is centered on the Nitrogen atom, while the carbon atom carries a lesser negative charge. This is in accordance with what would be expected from the observation that Nitrogen has a higher electronegativity and contributes more to the sigma and both pi-bonds. Furthermore, as this is an ion, the net charge will be -1, meaning that Carbon will be bearing some of that total negative charge, explaining the values seen to the left.
Molecular Orbital Analysis
To the left is a sample of five molecular orbitals from the cyanide ion. Carbon and nitrogen can be seen to have a bond order of 3, composed of one sigma (σ) and two pi (π) bonding regions between the atoms. With a charge of -1, each atom in the bond also has a lone pair of non-bonding electrons.
In the first example, the filled 1s orbital of nitrogen is considered as a molecular orbital. This MO is contributed to exclusively by the 1s atomic orbital of nitrogen. This orbital is extremely low in energy (-14.00393 au) and size, while being centered tightly around nitrogen's nucleus. The 1s orbital of carbon will result in a similar MO. Low level AO's such as these contribute negligibly to any MO or bonding character for the molecule.
Moving to more significant bonding orbitals, the first occupied σ bonding orbital of the carbon-nitrogen bond is featured second. This σ bond is a result of overlap between the 2s atomic orbitals of each atom. This MO is significantly higher in energy (-0.56195 au) as compared to the non-bonding 1s orbitals mentioned above. This MO has a significant bonding character as seen its composition between the atoms.
Considering the overlap of the 2s atomic orbitals again, there will also be a σ-antibonding (σ*) orbital resulting from these AO interactions. The σ* will be higher in energy (-0.10626 au) than its corresponding σ orbital (-0.56195 au) and has a significant antibonding character as seen in its high electron density behind either atom. This MO is filled in the ground state of CN-, cancelling the bonding effects of the σ orbital previously mentioned.
The bonding orbitals responsible for CN-'s bond order of three are those created in the overlap of the 2p orbitals. One of these overlaps (from 2pz) is head-on and results in a σ-bonding orbital, however the rest of the considerations for MO's will be regarding the resulting π-bonding orbitals from this overlap. This π-bonding orbital is featured below the σ* orbital to the left. The π orbitals, of which their are two with degenerate energies, have higher energies (-0.01696 au) than either σ/σ* orbitals (-0.56195 au and -0.10626 au respectively). These MO's have a high bonding character and are filled in the ground state, so they will contribute to molecular stability.
Corresponding with the π-bonding orbitals above, there are also two π-antibonding orbitals as featured in the fifth pane to the left. These antibonding orbitals are the result of the same 2p AO interactions as mentioned above. These orbitals are higher in energy (0.35435 au) than their bonding counterparts (-0.01696 au). As antibonding orbitals, they contribute to molecular destabilization due to their high electron densities behind each atom. In the ground state, they are not filled and as such, the corresponding π orbitals lower in energy can contribute to overall bonding in the ground state.