Minqi5318
Molecular Reaction Dynamics: Application to Triatomic systems
H +H1 System
Dynamic from transition state region
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
The transition state is defined mathematically as the saddle point on the potential energy surface, where ∂V(ri)/∂ri=0 (the gradient of the potential is zero). At the transition state, the second derivative of potential with respect to q1 is positive: ∂V2(q1)/∂q1 > 0, indicating a minimum of the curve; the second derivative of potential with respect to q2 is positive: ∂V2(q2)/∂q2 < 0, indicating a maximum of the curve. The coincidence of a maximum and a minimum indicates saddle point on the potential energy surface. It can be identified through finding the maximum on the minimum energy path linking reactants and the products. The Transition State's energy goes down most steeply along the minimum energy path linking reactants and products c.f. local minimum of the potential energy surface. [1]
Your description is confusing. Why do you switch between r and q for your partial derivatives? What are these variables? Referring to a plot will aid your description and avoid confusion in your terms and the structuring of your sentences. Sf3014 (talk) 11:58, 25 May 2020 (BST)
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with an “Internuclear Distances vs Time” plot for a relevant trajectory.
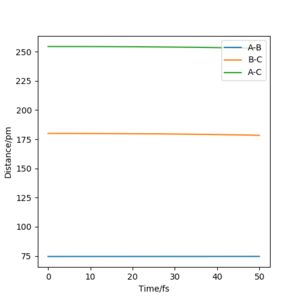
The best estemate of the transition state position rts = 91 pm
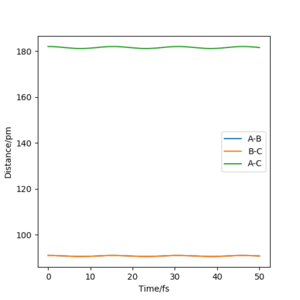
As shown in the Internuclear Distances vs Time Plot when rts = 91 pm above, when rts = 91 pm and p1 p2 = 0.0 g.mol-1.pm.fs-1, internuclear distance reamain (almost) constant, which shows that the molecule does not vibrate and stayed stably at the transition state forever.
Good effort but you could be more accurate (to 3 d.p) in your distances. Also, more description is missing on why the distances for AB and BC are equal. Sf3014 (talk) 12:03, 25 May 2020 (BST)
Comment on how the MEP and the trajectory you just calculated differ.
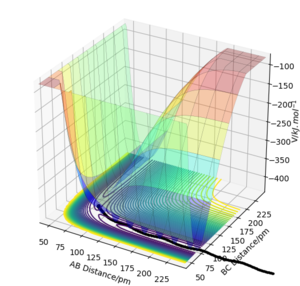
When r1=92 pm, r2=91 pm, atoms A and B dissociates. Using MEP calculation, AB dissociates through the minimum energy pathway and the dissociation ceased at a displacement much smaller than using Dynamic calculation. In Dynamic trajectory, kinetic energy was acquired during the trajectory from potential energy, therefore encourage inertial motion to proceed. In addition, MEP Calculation does not take into account the momentum of the particles, all the momentums are assumed to be zero.
Good but your discussion could be clearer your observations should be backed up with the right evidence and concluded for both calculations. Your provided evidence shows that there are oscillations in dynamic but not mep, so mention vibrational energy, and you can see your momenta is zeroing not zero because the trajectory still proceeds down the minimum pathway well. A better representation of your statement on momenta can be shown by your momenta vs time graph. Sf3014 (talk) 12:19, 25 May 2020 (BST)
When reversing r1 and r2, B and C dissociates while A and B sticks together. The final values of the positions are r1 (73.81819562) r2 (352.8544826) and p1 (3.258858751) p2 (5.06251673).
When setting up a calculation where the initial positions correspond to the final positions of the trajectory above, the same final momenta values but with their signs reversed, the reaction trajectory travels back to the orginal position r1 (91) and r2 (92) with p1= p2= 0.
Reactive and Unreactive trajectories
| p1 / g.mol-1.pm.fs-1 | p2 / g.mol-1.pm.fs-1 | Etot kJ.mol-1 | Reactive? | Description of the dunamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.28 | Yes | A-B + C → A +B-C | 
|
| -3.1 | -4.1 | -420.08 | No | A-B approaches C, but then leave without reaction occur | 
|
| -3.1 | -5.1 | -413.98 | Yes | A-B + C → A +B-C | 
|
| -5.1 | -10.1 | -357.28 | No | at TS region, strength of bondings A-B and B-C alternates, but eventually A-B leave intact (Barrier can be crossed, but then the system reverts back to the reactants) | 
|
| -5.1 | -10.6 | -349.38 | Yes | A-B + C → A +B-C at TS region, strength of bonding A-B and N-C alternates, but new product formed eventually | 
|
Good layout. However, showing the reaction equation is not a descriptions. Also, there is some confusion on your description of "A-B approaches C", (based on the the distances of r1 and r2, assuming q1 corresponds to r1 and so on) the reverse is true C approaches A-B. Your table would be clearer for the graphs that show distances AB and BC, if you defined q1 and q2 with respect to distances AB and BC. Sf3014 (talk) 12:35, 25 May 2020 (BST)
Conclusion: Reactants need to have a large enough ratio in the momentum to be reactive, ideally, p2 : p1 should be larger than 2 for the reactants to be reactive.
This is not true Sf3014 (talk) 12:35, 25 May 2020 (BST)
Transition State Theory
Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition State Theory often overestimates the reaction rate, compared to the results we calculated. Transition State Theory assumed that once the reaction has passed the Transition state and reached the product, it would not travel back to cross the Transition State and reverse to the reactant side. However, the calculations above showed that in practice, products can still recross the energy barrier to go back to the reactants. Even though the Transition State Theory ignored the effect of quantum tunneling, it's a relatively small contribution to rate in this case (small MW for H2). Therefore Transition State Theory tends to overestimate reaction rate values compare with experimental values.
Very good but what is a small MW? Also, where did you get this information from? A reference would be good Sf3014 (talk) 12:40, 25 May 2020 (BST)
F-H-H System
PES inspection
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 Reaction is exothermic. We can see there is a decrease in energy as H-H bond distance increases while H-F bond distance decreases. The clear downhill of the reaction path indicated exothermic reaction. Bond strength of H-H is 432 kJ/mol, while H-F bond strength is 565 kJ/mol. [2] Formation of H-F bond is preferred, as it would release more energy than the energy needed to break H-H bond.
H + HF Reaction is endothermic. H-H bond formed is weaker than the H-F bond, therefore energy needed to cross the activation energy barrier — endothermic.
According to Hammond Postulate, for an exothermic reaction, the TS resembles the reactants (early TS); for an endothermic reaction, the TS resembles the product (late TS). Therefore in this system, TS is very close to the H2 + F side (H-F distance much longer than H-H distance).
Very good. However you must refer to your graph clearly (ie label it with a figure number and state "see fig.x" in description) and define A, B and C. Sf3014 (talk) 12:45, 25 May 2020 (BST)
Locate the approximate position of the transition state.
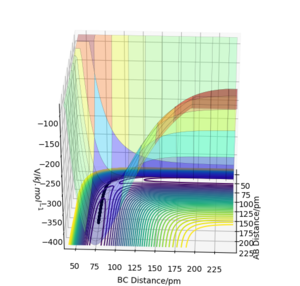
Position of the TS of H2 + F Reaction: rH-H=74.5 pm; rH···F=181.1 pm; At the TS, potential energy = 433.980 kJ/mol
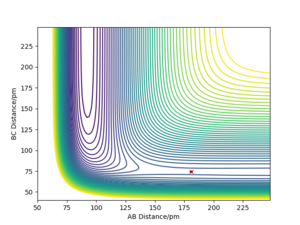
AB distance is the H-F distance, BC distance is the H-H distance.
Very good, but your this description on how you found this is in the wrong section, so this appears to lack description Sf3014 (talk) 12:48, 25 May 2020 (BST)
Report the activation energy for both reactions.
In the form of HF + H, potential energy =- 560.642 kJ/mol In the form o H2 + F, potential energy = -434.922 kJ/mol
Therefore compared with the TS potential energy (-433.980 kJ/mol): for HF + H to reach the TS, the activation energy is 126.02 kJ/mol; for H2 + F to reach the TS, the activation energy is 0.942 kJ/mol.
Very good Sf3014 (talk) 12:50, 25 May 2020 (BST)
Reaction Dynamics
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
For the exothermic reaction, in this case, the F + H2, energy is released into vibrational energy of product HF. When F approaches H, the repulsion between H-H is released. The released repulsive energy pushes H towards H and produces H-F vibration. [1]
This could be confirmed experimentally through Infrared Chemiluminescence. [3]The relative gain on many lines within several vibrational bands could be determined and hence direct measurements of the relative vibrational population in v = 0 can be obtained. We would, therefore, be able to see that the v=2 vibrational level is highly populated (strong peak at v = 2).
We could also use chemical laser to characterise the HF laser produced. Most of the HF is formed in the v=2 state, thus, the reaction creates an absolute inversion between v=2, v=1, and v=0. The output spectra of pulsed HF lasers showed that more than 60% of the reaction energy is released as vibrational excitation of the HF. [4]
Good but some visual aid would be great for you descriptions on the experiments. Also, how do you know the that the energy for the exothermic reaction is being converted into vibrational energy? Use the relevant plots from your simulations to support your statement Sf3014 (talk) 12:56, 25 May 2020 (BST)
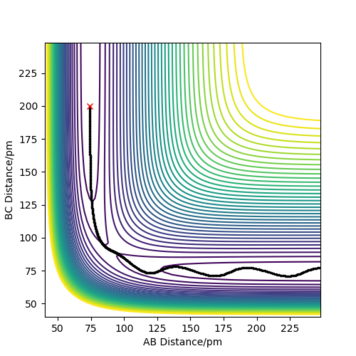
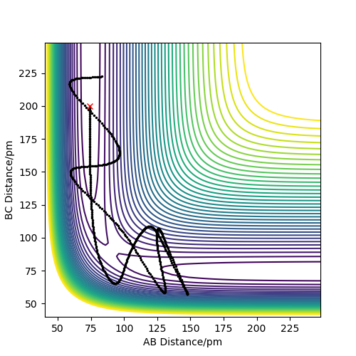
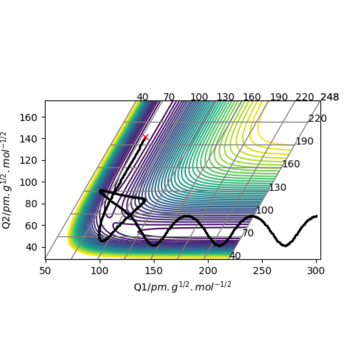
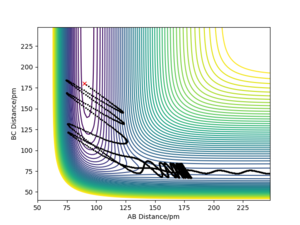
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
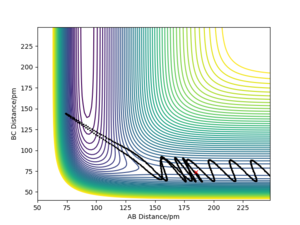
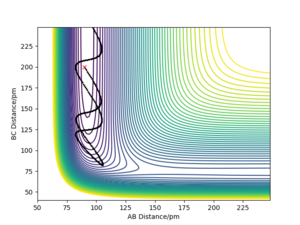
For H2 + F system, translational energy is more effective for activating the reaction: Under the conditions illustrated by Picture 1 below, activation barrier was easily crossed by applying translational energy, and the translational energy was converted into product's vibrational energy; c.f. under the conditions illustrated by Picture 2, even when a large amount of vibrational energy was put into the system, the reactants remain unreactive.
For HF + H system, vibrational energy is more effective for activating the reaction: Under the conditions illustrated by Picture 3 below, activation barrier was easily crossed by applying vibrational energy.
Translational energy is most effective for passage across an early TS, whereas reactant vibrational energy far in excess of the barrier height may be ineffective for reaction. Conversely, a late TS is best crossed by vibrational energy in the reactants. [1]
| H2 + F system (Early TS) | HF + H system (Late TS) |
|---|---|
 |
 |
 |
 |
This is perfect! Your description and link to evidence is very clear. Is this relationship know? Polanyi's rules should be mentioned Sf3014 (talk) 13:01, 25 May 2020 (BST)
Reference
- ↑ 1.0 1.1 1.2 Laidler, Keith J., in Chemical kinetics, 3rd ed., New York ; London, Harper & Row, 1987
- ↑ Carruth, Gorton, Ehrlich, Eugene. "Bond Energies." Volume Library. Ed. Carruth, Gorton. Vol 1. Tennessee: Southwestern, 2002.
- ↑ B. P. Levitt, ed. Physical Chemistry of Fast Reactions. Plenum Press, New York. SCHULZ, W. R., and LEROY, D. J. 1965.
- ↑ C. Bradley Moore, Laser studies of vibrational energy transfer, Accounts of Chemical Research 1969 2 (4), 103-109 DOI: 10.1021/ar50016a002