3.P3 Chemical Reaction Dynamics

A summary of a lecture course given by Dr. Laura Barter in Autumn 2012

Executive Summary

Lecture 1

A brief revision of inter-molecular interactions

The interaction potential determines whether or not it is possible for a reaction to occur, as in, whether or not there is sufficient energy in the system to break a bond and form a new one.

I'm sure we all remember that force is the derivative of potential:

$- F (r) = \frac{δ V (r)}{δ r}$

I'm sure we also all remember that the Born-Oppenheimer Approximation is a thing: that is, that because the electrons in a system move so much faster than the nuclei, we can treat their motions independently.

Potential energy surfaces model how energy changes as atoms move relative to one another. A 1D surface is sufficient to describe the interaction between two atoms or molecules, but if three or more are involved, the surface is multidimensional.

For a non-linear molecule of N atoms, the PES is dependent on 3N-6 independent co-ordinates (degrees of freedom).

There are several classical models we use for the interactions between atoms. There's the Coulomb interaction, used at 'long' distance:

$V (r) = \frac{Z_{1} Z_{2} e^{2}}{4 π ϵ_{0} r}$

There's the hard sphere model for 'short' distance, with no V until the spheres touch, at which point V=∞, and there is our old friend the harmonic oscillator, where we treat two atoms as though they are connected by a spring:

$V (r) = \frac{1}{2} k (r - r_{e})^{2}$

$- F (r) = \frac{δ V (r)}{δ r} = k (r - r_{e})$

And the Morse potential combines all of these together.

1D Potential Energy Surfaces

If we imagine a 1D potential energy surface as a Morse potential, there are some problems. There is no way for a bond to form stably because of conservation of energy, so there needs to be a third body to remove the excess energy. To simplify the model, we assume that all the molecules are moving along the same line.

2D Potential Energy Surfaces

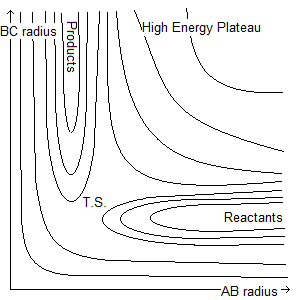
In the reaction:

AB + C ----> A + BC

We can use two parameters for the potential energy surface, the AB distance and the BC distance. This results in two valleys of potential at right angles to one another, with a high pass in between and a higher plateau in the angle between them. We can think of this as many Morse potentials all stuck together, with the minima forming the valleys.

Where T.S. is the position of the transition state.

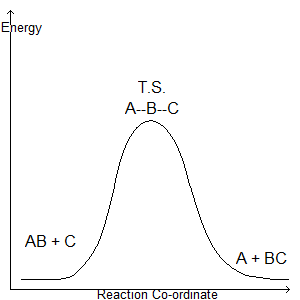
If a section is then taken through the lowest energy channel of this diagram, we obtain:

Which we recognise as a reaction co-ordinate.

It is possible for the reaction not to proceed despite molecules theoretically having enough energy. The total energy can be made up of translational and vibrational energy. This can be understood by thinking of the potential valleys as physical valleys. If there is too much vibration in the system initially (fluctuation in the BC radius), the 'ball' (the potential energy of the system, which moves along the surface) bounces off the head of the valley and returns, and the reaction does not proceed.

If there is an early transition state (one in the reactants' channel), translational energy (parallel with the x axis) is required to surmount it. An early transition state most resembles the reactants, so the incoming 'C' is the initiator of the transition state.

If there is a late transition state (in the products' channel) vibrational energy (parallel with the y axis) is required to surmount it. A late transition state most resembles the products, so the weakening of the AB bond (it vibrating) is what initiates the transition state.

Put more simply, an early transition state has its lowest energy path parallel to the x axis, and a late transition state has its lowest energy path parallel to the y axis. If the 'ball' has only x motion, it cannot travel in the y direction, and if it has only y motion, it cannot travel in the x direction.

This relates to the Hammond Postulate

Recap on Zero Point Energies

Due to the quantization of vibrational energies, even a molecule with with a vibrational quantum number of zero has some vibrational energy. This is called the zero point energy, and is defined by the following expression at ν=0.

$E_{v} = (ν + \frac{1}{2}) ℏ ω$

Where ω is the oscillation frequency.

How Zero Point Energies Apply Here

If either the reactants or the products have a lower zero point energy, the reaction profile is tilted, so either the products or the reactant is lower in energy. If it's the reactant that is lower in energy, an early transition state will also be lower in energy, whereas a late transition state will barely be affected. If it's the product that is lower in energy, a late transition state will also be lower in energy, whereas an early transition state will barely be affected. We can think of this as 'tilting' the reaction profile, but that isn't necessarily helpful.

Summary

In this lecture we:

Revised the models that, in combination, give us the Morse potential.
Discussed the problems with the 1D potential energy surface for chemical reactions.
Looked at the 2D PES, and how this relates to the Hammond postulate and the reaction profile.
Saw how the distribution of internal energy between vibrational and translational modes affects reactivity.
Saw how the zero point energy of reactants or products affects the reaction profile.

Lecture 2

Revision of Arrhenius

We all remember the Arrhenius equation:

$k (T) = A e^{\frac{- E_{a c t}}{k_{b} T}}$

This means that the rate depends on molecules being 'activated', as in having a threshold energy. This strongly suggests the existence of transition states: the transition state is the reactant once it has achieved threshold energy.

In addition, we should remember that a transition state is an energy maximum, as distinct from an intermediate. An intermediate is an energy minimum that is neither the products nor the reactants.

How long do chemical reactions really take?

If we think about reactions in terms of bond making and breaking, then we can calculate how long the reactions take. A bond with an oscillation frequency of 3000cm^-1 will stretch and relax once every 10¹⁴s<sup-1, so it will reach its longest distance in half that time, which is once every 5fs. The RDS can be defined as the time it takes for the molecules to encounter one another in the correct geometry. If it's on a fs timescale, though, how can we observe transition states?

Creating and Detecting the TS

We have the stopped flow method, where reagents are injected suddenly into a chamber, where the reaction is then monitored spectroscopically. This has its problems because it relies on diffusion, which is a bit slow and rubbish, so the timescale is really rather long (about 1ms).

There is also thermodynamic triggering, where an equilibrium system is suddenly raised 5-10^oC in 1μs, or even 1-100ns, depending on the method used. The system is then observed as it reaches a new equilibrium. This method can also be used with sudden changes in pressure. The problem here is that the timescale is still a bit long: thermal diffusion is still too slow. Also, this method can't be used to irreversible reactions.

We can also apply strong electric potentials to shift the energy levels of molecular systems, and so trigger reactions. This still works too slowly, and requires very high voltages to make it work.

So instead, we use lasers! These can be pulsed on a fs scale, so we can do time resolved spectroscopy. The laser optically excites the reactants, causing the reaction to start.

Dissociation of Sodium Iodide

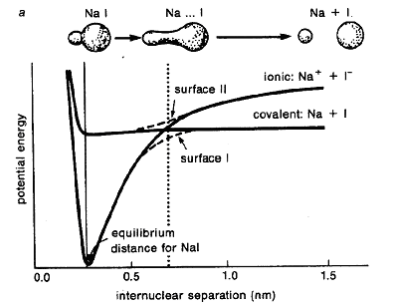
The dissociation of NaI occurs via light exciting the system into an antibonding orbital. The PES looks like this, with the lower line the bonding orbital, and the higher line the antibonding (excited) orbital.

The thick black lines are simple, approximate energy surfaces. The dashed lines that avoid the two surfaces crossing show the real state. PES of the same symmetry are not allowed to cross, as it is forbidden by quantum mechanics. Instead, the two orbitals mix where they are close in energy, causing splitting, with which we are all familiar from MO theory.

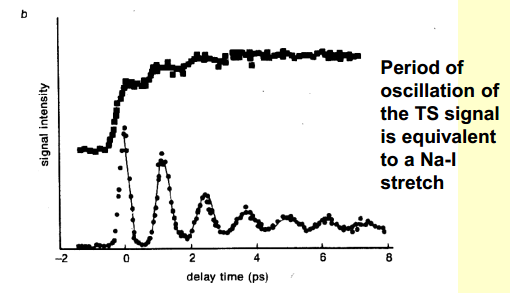
There is something else of note in the NaI example, shown in the graph below.

The top line represents the laser, and the bottom line represents the spectroscopic response, that is the dissociation of the reactants. When the laser pulse is turned on, at time 0, there is a spike in the spectroscopic response, that is the concentration of the products. We would expect this. What classical physics would not expect, however, is the multiple peaks afterwards. We might predict that the shape of the lower line would follow the shape of the first.

Summary

In this lecture we:

Had another look at the Arrhenius equation
Discussed the methods of observing reactions in real time, and the problems with each.
We saw that PES are not allowed to cross if the symmetry is the same.
We saw that the dissociation of NaI does not correspond to classical predictions.

Lecture 3

Revision: Quantum and the wavefunction

We remember, of course, the time independent Schrödinger equation.

$\frac{ℏ^{2}}{2 m} \frac{δ^{2} ψ (x)}{δ x^{2}} + V (x) ψ (x) = E ψ (x)$

Where ψ is the wavefunction of the particle. This is possible owing to particle-wave duality. The absolute value of the wavefunction squared gives the probability of finding the particle at any one point.

The Time Dependent Schrödinger Equation

We need the time dependent Schrödinger equation because we're considering molecules over a period of time: obvious when you think about it. It looks like this:

Failed to parse (syntax error): {\displaystyle i\hbar \frac{\delta \psi (x,t)}{\delta t} = \frac{-\hbar^2}{2m}\frac{\delta^2 \psi (x,t)}{\delta x^2} + V(x)ψ(x,t) }

ψ(x) can be related to ψ(x,t) quite simply:

$ψ (x, t) = e^{\frac{- i E t}{ℏ}} ψ (x)$

This gives us a wavefunction with a real and an imaginary part, π/2 out of phase with one another, showing that it oscillates at a frequency corresponding to E=hv. The wavefunction oscillates, but the observable properties do not. The absolute value of ψ is constant, meaning that the real and imaginary components fluctuate, but they always come to the same absolute value, like a line of constant length rotating around the origin. The wavefunction is time dependent, but the expectation value (the mean) is not, meaning that the observable properties are time independent.

Wavepackets

By mixing together time dependent wave functions (much like LCAO, but time rather than space), we can get a time dependent wavepacket. This looks like:

$Ψ (x, t) = \frac{1}{\sqrt{2}} [e^{\frac{- i E t}{ℏ}} ϕ_{1} (x) + e^{\frac{- i E t}{ℏ}} ϕ_{2} (x)]$

The expectation value is:

$< x_{(t)} > = \int Ψ x Ψ^{*} d x$

Or:

$< x_{(t)} > = \int \frac{1}{\sqrt{2}} [e^{\frac{- i E t}{ℏ}} ϕ_{1} (x) + e^{\frac{- i E t}{ℏ}} ϕ_{2} (x)] x \frac{1}{\sqrt{2}} [e^{\frac{+ i E t}{ℏ}} ϕ_{1} (x) + e^{\frac{+ i E t}{ℏ}} ϕ_{2} (x)] d x$

Which then becomes:

$< x_{(t)} > = \frac{1}{2} \int (x ϕ_{1}^{2} d x) + \frac{1}{2} \int (x ϕ_{2}^{2} d x) + \int (x ϕ_{1} ϕ_{2} d x) c o s (ω_{1} - ω_{2}) 2 π t$

The first two terms are time independent (as we can see, given they have no t component) but the last is time dependent, and ω values are frequencies of eigenstates 1 and 2 respectively.

We can see here that adding the two wavefunctions together gives us a time dependent term in the expectation value, meaning that the observed behaviour is time dependent! Yay!

This superposition is called a wavepacket!

There are two kinds of waves in quantum:

Standard waves (standing waves, time independent, eg. particle in box)
Wavepacket (travelling packet of probability, time dependent)

A single vibrational eigenstate doesn't oscillate over time in a classical sense. The nuclear position isn't defined as a function of time, and so nuclear separation is smeared out, like an electron in an MO.

A vibrational wavepacket behaves somewhat like a classical oscillator, and does more the more eigenstates you add up. This means that the nuclei have well defined position, but not necessarily momenta (as in, uncertainty principle), and the position is better defined the more eigenstates you add up. This means that a big energy distribution results in a 'tight' wavepacket, one very well defined (and thus short) in time. A Gaussian wavepacket is a good representation of a particle moving through free space.

Summary

Here we saw:

Eigenstate solutions to the time dependent Schrödinger equation don't give time dependant observable properties (the expectation value is still time independent)
In order to get time dependent expectation values, we must sum eigenstates.
The more eigenstates we add together, the better defined the particle's position is with respect to time, but the worse defined it is wrt position.

Lecture 4

How does this apply to reactions?

If we're acting on a very short timescale (as we have to be, when trying to see intermediates), we have to know very precisely where our photons are. In order to know where our photons are, we have to use a wide spread of frequencies. A wide spread of frequencies excites more than one vibrational state of NaI, thereby creating a vibrational wavepacket.

Vibrational wavepackets are observed even if a molecule is solvated. Reaction dynamics are affected by solvent atoms.

Solvent atoms and reactivity

Solvents exert an important influence on bond making and breaking. They can act as 'chaperone' molecules, to stabilise charged species, or trap atoms in solvent cages to encourage bond making. We can probe these things using fs spectroscopy.

The solvent can provide a 'barrier' on the potential energy surface for dissociation: that is, the atoms moving away from each other 'bounce' off the solvent atoms in order to recombine. If the initial molecule is sufficiently excited, however, this solvent barrier is not a problem.

So what happens to the wavepackets where the reactants 'bounce' back together? The energy is transferred to solvent via collisions, or dissipates to the rest of the system (i.e. to other bonds in the molecule). Thermal equilibrium is reached when the energy imparted by the laser has spread to the whole system. The exchange energy is a measure of the energy flow between bonds. This gives an idea of how quickly free energy can be lost by the system to get stable products out. The total temperature rise is small, but the optical excitation causes vibrational excitation that would require very high temperature for an equivalent result.

Wavepacket interactions with the environment

The wavepacket interacting with the 'thermal bath' environment causes energy exchange, making the wavepacket collapse into eigenstates. The wavepacket can impart energy to the surroundings and also receive energy from them.

Wavepackets and reactivity

Vibrational wavepackets can tunnel through potential energy barriers: in the simple harmonic oscillator, there is a 'leaking' of probability out of the sides of the potential well. This is talking about nuclei tunnelling, not electrons. If the wavepacket is high enough in energy, it can just mosey over the top of a barrier, but if it's just below the barrier in energy, there's still a probability of it getting through (because the wavepacket is a distribution of energies, and some of them will be high enough to surmount the barrier).

Back to NaI

We see the PES diagram above, and we can see that on the excited state PES, there is a barrier to overcome for dissociation to occur. Each time the wavepacket hits the barrier, some of it tunnels through, and the rest is reflected back. The same fraction will tunnel on the second encounter, and this is why we see the multiple peaks in the spectrum: the bond has to be at its fullest length in order to dissociate, as in, in order for the wavepacket to hit the barrier.

Summary

In this section we learnt:

When we optically excite a molecule on a fs timescale, we're creating a wavepacket.
Solvent molecules affect reaction dynamics by creating a 'solvent barrier' on the PES, inhibiting dissociation.
Energy from excited molecules disperses into the system by collisions between molecules, and vibrations in other bonds in the molecule.
If a wavepacket is excited high above potential energy barriers, it can just sail over.
If the wavepacket is a little lower in energy, it can 'tunnel' through, a small percentage going through, while the rest bounces off.
This 'bouncing' behaviour explains the multiple peaks in the NaI study.

Lecture 5

It's not as simple as that

Sometimes reactions are dominated by just one or two of hundreds of vibrations, which are all similar in energy. This means that only a couple of the vibrations are 'relevant' for the reaction to occur, and the others have no impact on whether or not the reaction occurs. This means that we don't see the peaks that are visible in the dissociation of NaI, because the majority of the wavepacket is irrelevant to the reaction, and the picture becomes a lot more chaotic.

To make this better, we look at the statistical mechanics rather than just the quantum.

Statistical Mechanics and Reactivity

So far we've discussed systems that aren't in equilibrium. Now we move to some that are. Where systems have hundreds or thousands of vibrations contributing to reactivity, they are all in equilibrium with one another, with products and reactants, and we simply can't ignore that.

The Gibbs free energy determines the equilibrium constant, thus:

$Δ G = - k T l n K$

But remember, children, the Gibbs free energy is made up of both enthalpic and entropic contributions! We must invoke statistical thermo to deal with these entropies.

If we have a system that has no enthalpy gap between reactants and products, with a singly degenerate reactant state, and a triply degenerate product state, we can see that the K_eq will be 3. Entropic states make a difference to our Gibbs energy, according to:

$Δ G = Δ H - T Δ S$

We can put these equations together to get an expression for the equilibrium constant in terms of entropy.

$K = e^{\frac{- Δ G}{k T}} = e^{\frac{- Δ H + T Δ S}{k T}} = e^{\frac{- Δ H}{k T}} \cdot e^{\frac{Δ S}{k}}$

The Boltzmann formula for entropy is:

$S = k l n Ω$

And if we substitute this in to the above:

$K = e^{\frac{- Δ H}{k T}} \cdot e^{l} n Ω_{2} - l n Ω_{1}$

Which simplifies to:

$K = \frac{Ω_{2}}{Ω_{1}} e^{\frac{- Δ H}{k T}}$

There we have it: the equilibrium constant is dependent on the degeneracy of product and reactant states! Hurrah!

Transition State Theory

Transition state theory is used to make an expression for the thermal rate constant. It only looks at the statistical properties of systems, not details of molecular collisions. To do this, it assumes some things.

Nuclear and electronic motion are separate
The molecules follow the Boltzmann energy distribution
Systems that have crossed the transition state can't cross it again.
Motion along the reaction co-ordinate can be treated as translation.
Transition states all follow the Boltzmann distribution, even if reactants and products aren't in equilibrium.

We define a small area (of thickness δ) at the maximum of the reaction co-ordinate curve, and call that the transition state. We call it the 'dividing surface'. In the 2D PES, it's at right angles to the reaction pathway.

So we have an equilibrium: A + B ⇋ X* ⇋ C

If this is true, we have two kinds of transition state: the kind that will become C (N*_f) and the kind that will become A + B (N*_b). And so:

$N *_{f} + N *_{b} = N *$

$K * = \frac{[N *]}{[A] [B]}$

$N *_{f} + N *_{b} = N * = K * [A] [B]$

At equilibrium, rate forward must equal rate backward. The steady state approximation says that the concentration of the transition state mustn't change, so at equilibrium: $N_{f} * = N_{b} *$

If we assume that there is no re-crossing from the products to the reactants, then we can say that N*_b = 0, because there is no contribution to the concentration of the transition state from the backwards reaction. This means that N* = N*_f. Neglecting the backward component of the concentration of the transition state means that it is now described by: $N * = K * \frac{[A] [B]}{2}$

To get our rate, we need to define the rate at which N* crosses the barrier, or $\frac{δ N *}{δ t}$ . As we're defining the reaction solely as a translation, we can define this as the time taken for the transition state to cross the distance δ, or $δ t = \frac{δ}{ν_{s}}$ , where ν is average speed with which the transition state crosses δ. This leaves our overall expression as:

$\frac{d N}{d t} = δ N * \frac{ν_{s}}{δ}$

As we defined above, the number of transition states crossing δ in the direction of the products is half the total number of transition states. This means the above equation should really be written:

$\frac{d N}{d t} = \frac{δ N *}{2} \frac{ν_{s}}{δ}$

The average velocity of the transition state moving in one direction (eg. forward!) is $ν_{s} = (\frac{2 k_{b} T}{π ν_{s}})^{\frac{1}{2}}$

If we substitute this in, we obtain:

$\frac{d N}{d t} = \frac{N *}{2} (\frac{2 k_{b} T}{π μ_{s}})^{\frac{1}{2}} \frac{1}{δ}$

From statistical mechanics, we can get an expression for the equilibrium constant which it is then possible to rearrange for N*.

$K * = \frac{N *}{[A] [B]} = \frac{Q *_{t o t}}{Q_{A} Q_{B}} e x p (\frac{- E_{0}}{k_{B} T})$

$N * = \frac{Q *_{t o t}}{Q_{A} Q_{B}} [A] [B] e x p (\frac{- E_{0}}{k_{B} T})$

We can then substitute this into our dN/dt expression from earlier:

$\frac{d N}{d t} = (\frac{2 k_{b} T}{π μ_{s}})^{\frac{1}{2}} \frac{1}{2 δ} \frac{Q *_{t o t}}{Q_{A} Q_{B}} [A] [B] e x p (\frac{- E_{0}}{k_{B} T})$

Of course (of course!) this is not the end of the matter. Q_tot* can be expanded further, as translational motion is separable (remember?). Therefore, $Q_{t o t} * = Q_{s} Q *$ where Q_s is the partition function for reaction coordinate motion, and Q* is the partition function for everything else. The translational partition function for motion in one dimension in a system of length δ is:

$Q_{s} = (2 π μ_{s} k_{B} T)^{\frac{1}{2}} \frac{δ}{h}$

So we substitute THAT in:

$\frac{d N}{d t} = (\frac{2 k_{B} T}{π μ_{s}})^{\frac{1}{2}} \frac{1}{2 δ} (2 π μ_{s} k_{B} T)^{\frac{1}{2}} \frac{δ}{h} \frac{Q *}{Q_{A} Q_{B}} [A] [B] e x p (\frac{- E_{0}}{k_{B} T})$

Cancel out some stuff, and we're left with:

$\frac{d N}{d t} = \frac{k_{B} T}{h} \frac{Q *}{Q_{A} Q_{B}} [A] [B] e x p (\frac{- E_{0}}{k_{B} T})$

The term with all the Qs is the ratio of states, that is, the available states of product, divided by the available states of reactants A and B. If we have a careful look, as well, we can see something remarkable. The rate of a simple A + B → C reaction is given by rate = k[A][B], and this expression above, if we squint, follows this form exactly. This means we've found an expression for our rate constant, k!

Hurrah!

$k = \frac{k_{b} T}{h} \frac{Q *}{Q_{A} Q_{B}} e x p (\frac{- E_{0}}{k_{B} T})$

The first term (k_BT/h) is the 'frequency factor', having units of s^-1. Physically, it means the speed at which the bond breaks, or the speed of bond vibration! We've already mentioned the ratio of states term. The final term is the Boltzmann term.

To evaluate the equation, we need to calculate the partition function Q*, which can be really rather complicated. However, it can still work well for some simple systems.

Summary

Transition state theory requires a lot of approximations, but gives an expression for the rate constant.

Lecture 6

The Failings of TS Theory

TS theory assumes that thermal activation is the only means of surmounting the potential energy barrier. This ignores the existence of tunnelling, which is important particularly for low mass particles, eg. electrons, protons.

TS theory assumes that the moving of reactants across the transition state corresponds with a simple translation, but this is true only for weakly bound transition states. This means that the maximum of the reaction co-ordinate isn't necessarily flat, which means that the TS has a rather different partition function.

TS theory assumes, as we saw up the page, that the system passes through the transition state only once, and that there is no recrossing from products to reactants. This is demonstrably not the case in many reactions.

TS theory assumes that reactants and TS are in equilibrium. If they aren't, this makes the partition function quite different.

TS theory assumes that the reactants and products correspond to the Boltzmann distribution, but this is not always the case. Some vibrational modes are more closely linked to the reaction path than others, meaning that there will be 'depletion' from these states as they go on to react. Things will only correspond to Boltzmann if relaxation is fast compared to reaction rate.

TS theory assumes that crossing the TS barrier is the RDS, but this is not always the case. Sometimes the rate of collision is the RDS.

Lindeman Theory

Lindeman suggested that molecules become energised by bimolecular collisions, and this energy enables them to pass over the TS barrier. The dissociating products carry away excess energy. This theory explained experimental observations that unimolecular gaseous reactions change from first to second order when going from high to low pressure.

Why was everyone confused? Well, if collisions providing sufficient energy is the RDS, how is the reaction ever first order? Collisions require two molecules to occur.

In the following, the presence of a * denotes a transition state that has obtained sufficient energy from its surroundings to turn into products.

The overall mechanism is made up of three reactions:

A + M → A* + M rate given by $\frac{d [A *]}{d t} = k_{a} [A] [M]$

A* + M → A + M rate given by $\frac{d [A *]}{d t} = - {k_{a}}^{'} [A *] [M]$

A* → P rate given by $\frac{d [A *]}{d t} = - k_{b} [A *]$

So the overall rate, equated to zero because of the steady state approximation, is:

$\frac{d [A *]}{d t} = k_{a} [A] m - {k_{a}}^{'} [A *] [M] - k_{b} [A *] = 0$

And then rearrange:

$[A *] = \frac{k_{a} [A] [M]}{{k_{a}}^{'} [M] + k_{b}}$

And we know that the rate of production of the product is $\frac{d P}{d t} = k_{b} [A *]$ , meaning that the rate in terms of the reactants is:

$\frac{d P}{d t} = \frac{k_{b} k_{a} [A] [M]}{{k_{a}}^{'} [M] + k_{b}} = k_{u n i} [A]$

At high pressure, [M]→∞, meaning that ${k_{a}}^{'} [A *] [M] > > k_{b} [A *]$ , meaning that the RDS is the rate of passage through the transition state. We can thus ignore the k_b in the denominator, meaning that our rate law looks like:

$\frac{d P}{d t} = \frac{k_{b} k_{a} [A]}{{k_{a}}^{'}}$

And lo, it is first order!

At low pressure, ${k_{a}}^{'} [A *] [M] < < k_{b} [A *]$ , making the RDS is the activation of the reactants by collisions. We can thus ignore the k_a[A*][M] term in the denominator, giving a rate law of:

$\frac{d P}{d t} = k_{a} [A] [M]$

Voila! Second order!

This gives very good agreement with experiment.

Oh, Kramers

Lindeman theory works well for gaseous cases, but in liquid or solid phases, it is more complex. Rather than the RDS being the thermal activation of the reactants, it's the transfer of the remaining thermal energy to the surroundings. The release of this energy is impeded as the energy can't be lost as kinetic energy: motion is hindered by the solvent cage or the solid matrix.

Kramers came up with theory of reactants in solution. It takes into account the inevitable re-crossing of the transition state that occurs in solution. It visualises the system as a 1D PES, as we're used to, but with the maximum a bit like Brownian motion, described by the Langevin equation. It also introduces a 'damping force' to account for the effect of solvent.

The damping force is proportional to velocity along the reaction co-ordinate and the friction constant β (increasing with solvent density, pressure and viscosity). It represents the exchange of energy between the reaction co-ordinate and the bath.

Kramers assumed that the PES had a harmonic shape and that frictional forces were sufficiently strong that energy equilibration was ensured. The Langevin equation represents the behaviour of an harmonic oscillator under the influence of fluctuating forces (from the thermal bath). This gives a Kramers transmission coefficient, κ^KR, by which we multiply the TS theory rate constant to get an even better rate constant!!!

Failed to parse (syntax error): {\displaystyle κ^{KR} = (1 + (\frac{\beta}{2\omega*})^2)^\frac{1}{2} - \frac{\beta}{2\omega*} }

Where ω is the frequency of the harmonic oscillator representing the TS, and β is the friction constant from above.

The Conflicts with TS theory

In cases of intermediate friction, where β<<2ω*, κ = 1, as in a normal gas phase reaction, TS theory holds. Collisions with solvent are sufficient to maintain equilibrium distribution of activated reactants, but insufficient to perturb passage over the PE barrier. In cases of high friction, where β<<2ω*, $κ = \frac{ω *}{β}$ , collisions with solvent lead to re-crossing of PE barrier before stable product formation, and the rate is lower than the transition state theory prediction. Barrier re-crossings become so frequent that the rate can be an order of magnitude lower than predicted by TS. In cases of low friction, an equilibrium distribution of reaction states can't be maintained. This means that the activation of reactants becomes the rate limiting step.

Summary

TS theory is sometimes rubbish
The Lindeman mechanism can explain why reactions sometimes appear first order, and sometimes second.
Kramers theory introduces a frictional constant, which modifies the TS theory prediction to give a more accurate result.

Lecture 7

Electron Transfer Reactions

In electron transfer reactions, no bonds are made or broken. This means we need a different picture of the reaction. Electron transfer is achieved by tunnelling between molecules, from one potential well to another, even though the electron doesn't classically have sufficient energy to surmount this barrier. Because electrons are such low-mass particles, they have a long wavelength, making them good tunnellers, as it's quite possible for the wavefunction to stretch across the potential barrier into the next well. In the simplest case (with PE barrier height V, distance r, mass of electron m, and exponential coefficient β, measure of electron's tunnelling ability):

$H_{A B}^{2} \propto e x p (\frac{- 2 r \sqrt{2 m V}}{ℏ}) = e x p (- β r)$

H_AB is the electronic coupling: the energy of interaction between D and A states, related to the square of the integrated overlap of D and A wavefunctions. We have met it in last year's quantum course as the overlap integral.

There is no temperature term because in this model the well is 'deep', that is, the barrier is in the region of eV in magnitude, whereas thermal energies are in the region of 25meV in magnitude. Experimentally, we see temperature dependence at high T, but at low T it is temp independent, meaning the tunnelling mechanism predominates.

β, the electron tunnelling ability, is dependent on the availability of electrophiles. In a conjugated pi system, β = 0, and transmission is instantaneous. The bigger the gaps between electron density, the larger β is, and the lower the penetration of electrons beyond the barrier. The highest non-adiabatic electron transfer rate is 100fs (or 10¹³s^-1: this is long enough for all vibrations to have gone through one vibrational period. The limit is the time taken for nuclear reorganisation ( related to FC factor). Distance is still the dominant effect on ET rate. The VdW radius for most systems is 3Å.

The Franck Condon Factor

In order for electron transfer to form products there has to be some nuclear rearrangement. This depends on the overlap between the vibrational wavefunctions of the ground and excited electronic states.

$F C = \int ϕ_{v} (r e a c t) ϕ_{v} * (p r o d) d r$

This is effectively a measure of similarity between the structures of the reactants and the products. The value is between 0 and 1, because the wavefunctions are normalised. If the FC = 1, the structures are identical, and if it's 0, there is no overlap at all. Transition only occurs when the nuclei satisfy both electronic wavefunctions at once.

Fermi's Golden Rule

$k_{e t} = \frac{2 π}{ℏ} H_{A B}^{2} F C$

k_et is the electron transfer rate constant. The FC factor includes temperature dependence, and includes, as mentioned above, the nuclear poisition. The overlap integral is the electronic contribution. This equation only applies in non-adiabatic cases (cases where heat is exchanged between system and surroundings, and D and A are well separated and distinct)

Using Fermi's golden rule, and the above section, we get this equation for the rate constant:

$k_{e t} = 1 0^{13} e x p (- β (r - 3))$

Because 10¹³s^-1 is the fastest that these transfers can occur.

This is why we have multiple transfers (or hops) instead of one long transfer: much more efficient.

Summary

Electron transfer reactions rely on electron tunnelling (a lot)
Their rate can be described by the depth of the potential well and the distance between the wells
The Franck Condon factor describes the similarity of the product and reaction structures
Fermi's golden rule relates all these together to give a rate constant.

Lecture 8

Other things to consider

The Franck Condon factor demonstrates the extent to which R and P share geometry, but it doesn't explain how that happens or why it stays there. In addition, we need to consider the role of solvent, which as charges move from products to reactants, take time to adjust to this new configuration. This can result in the potential energy barrier increasing, or decreasing. This is in opposition to the conservation of energy!

The extra energy must dissipate somehow, for example through frictional forces. The wavepacket damping we saw up the page was an example of this. This means we need to consider the whole system, thus the FC factor has to be integrated over all degrees of freedom. This can be very very complicated, especially if many bond lengths need to change. If, however, only one or two bonds are affected by charge reorganisation, it can be a bit simpler.

Imagine we have two parabolic 1D potential energy surfaces. In the non-adiabatic case, there is weak coupling, and the overlap is a simple crossing of lines. In the adiabatic case, where coupling is strong, the upper lines curve together and so do the lower lines, meaning the system can cross from the lower surface of the reactants to the lower surface of the products.

Alas, this doesn't always work, because the entropic contribution can be very large indeed, meaning that potential energy alone isn't sufficient to predict reactive behaviour.

Entropy is difficult, so we eliminate it. We define K as the ratio of probabilities of product states to reactant states. If we assume that the reactants are in the most common enthalpy state, then we have $K = \frac{P r o b Δ H_{1}}{P r o b Δ H_{m} a x}$ . The probabilities, according to central limit theorem, can be expressed as a Gaussian function of form $P r o b = e^{- A Δ H_{1}^{2}}$ , then $K = e^{- A Δ H_{1}^{2}}$

If we then substitute that expression into $Δ H = - k T l n K$ , then:

$Δ G = - k T l n e^{- A Δ H_{1}^{2}} = k T A Δ H_{1}^{2}$

In this model, the Gibbs free energy when plotted against the enthalpy gives a simple harmonic oscillator. This will happen as long as the system is strongly coupled to the bath and the random fluctuations have enough time to average out (otherwise a Gaussian function won't accurately describe the average enthalpies). This means that the reaction must be slow relative to the thermal exchange between system and bath. If this is not the case, we have to use a multi-D PES.

The Arrhenius Interpretation

If T is high enough, of course, tunnelling isn't a major contributor to the FC factor. We can use the Arrhenius picture instead, with the free energy of activation given by height of barrier above reactant energy (like activation energy, but different because we're talking about free energy surfaces rather than reaction co-ordinates). Remember the Arrhenius equation? Here it is applied to free energy surfaces:

$k = A e x p (\frac{- Δ G *}{k_{B} T})$

Marcus Theory

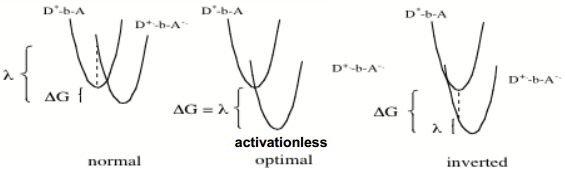
Both our surfaces are quadratic, and we know the relationship between ΔG (the free energy of reaction, the y distance between the minimum reactants and the minimum products), ΔG* (the free energy of activation, the y distance between the minimum reactants and the intersection of the two lines) and λ (the reorganisation energy, the y distance between the product line over the reactant minimum and the product minimum).

$Δ G * = \frac{(λ + Δ G)^{2}}{4 λ}$

The reorganisation energy depends on how much nuclear and dipole rearrangement occurs between reactants and products. The greater the reorganisation, the greater the reorganisation energy.

Put the above equation together with the Arrhenius equation and this is the result:

$k_{E T} \propto F C = A e x p (\frac{- (λ + Δ G)^{2}}{4 λ k T})$

Look, it's temperature dependent! This equation make the prediction that greater ΔG doesn't always correlate to increased rate: there is a point beyond which rate decreases again, known as the inverted region. This can be explained by visualising the curves, thus:

In the Marcus (Classical) picture, the Gaussian distribution becomes infinitely narrow as the temperature → 0, whereas in the quantum picture, until T > ħω/2ksub>B, there is little temperature dependence. Experimental evidence suggests that nuclei must tunnel through the barrier between reactant and product structures.

Summary