3.O4 Introduction to Organic Physical Chemistry

A summary of a lecture course given in Autumn 2012 by Prof. Iain McCulloch at Imperial College London.
What's up with these reaction mechanisms anyway?

Executive Summary

The Gibbs free energy, enthalpy and entropy of the transition state have an influence on the rate of reaction:

$Δ G^{‡} = Δ H^{‡} - T Δ S^{‡}$

The substituent constant, σ, tells us whether a substituent is electron donating (negative value) or electron withdrawing (positive value).
The reaction constant, ρ, tells us whether the rds of a reaction creates positive charge (negative value) or negative charge (positive value).
In a Hammett plot, σ is the x axis and ρ is the gradient.
If the Hammett plot bends up, there is a change in the mechanism.
If the Hammett plot bends down, the rds in the mechanism has changed.
Relative acidities affect the position of equilibrium.
Solvents can have a big impact on reactivity.
The Hammond postulate states that a transition state looks most like the state it is closest to in energy.
Isotopic effects can be used to determine the mechanisms of reactions. If a Primary Kinetic Isotopic Effect is observed, the isotope is involved in bond formation or cleavage in the rds.
Specific acid and base catalysis are catalysis by H⁺ and OH^- respectively. They are fast steps.
General acid and base catalysis are catalysis by undissociated acid and base. They are generally slow, and may be the rds.
Electrophilic catalysis is by aprotic acids, and proceeds by co-ordinating, either to free OH^- or to the reactants to increase reactivity.

Lecture 1

A brief revision of Thermodynamics and Kinetics

Kinetics: the study of rate as a function of a variable, like concentration, pH, etc.
Recall the equilibrium constant:
$K = \frac{[P r o d u c t 1] [P r o d u c t 2]}{[R e a c t a n t 1] [R e a c t a n t 2]}$

This links, as I'm sure we all remember, to the ΔG via:
$Δ G = R T l n K$

$Δ G = Δ H - T Δ S$

And if this is applied to the transition state, it becomes:
$Δ G^{‡} = Δ H^{‡} - T Δ S^{‡}$

ΔG⁰ is the total difference in energy between reactants and products. ΔG^‡ is the activation energy. ΔG⁰ + ΔG^‡ = total distance from the energy maximum to the energy minimum of a system (assuming only one transition state).

In solution:
$E_{a c t} = Δ H^{‡} + R T$

But around standard conditions, RT is really small, so:
$E_{a c t} \approx Δ H^{‡}$

The activation energy relates to the equilibrium constant via the Arrhenius equation:
$k = A e^{\frac{- E_{a}}{k_{B} T}}$

Rate is (usually) defined as the change in concentration of a species with respect to time, eg:
$R a t e = \frac{d [R e a c t a n t 1]}{d t}$

Applying these to rate

Rate depends on the proportion of particles that have activation energy. By making the activation energy lower, we increase the proportion of particles that have the necessary energy, therefore:

Increased T increases rate
Lower ΔH^‡ increases rate
More positive ΔS^‡ increases rate

In practice ΔH^‡ is almost always positive, and isn't super helpful for determining mechanisms, so instead we use ΔS^‡, which varies a lot, and can help discriminate between potential mechanisms. If ΔS^‡ is positive, our TS is less ordered than the reactants. If it is negative, the TS is more ordered than the reactants.

S_N1 and S_N2

In the S_N1 reaction, the r.d.s. is the dissociation of the leaving group. This means that the transition state has a longer Reactant-LG bond, meaning it is 'floppier', thus having more degrees of vibrational freedom, and thus having a higher entropy, so ΔS^‡ is really rather positive.
In the S_N2 reaction, with its associative mechanism, the TS has two long bonds, one to the incoming group and one to the leaving group. This means that the TS has fewer degrees of rotational and translational freedom, making ΔS^‡ negative.
And so we can see the difference between S_N1 and S_N2 reaction mechanisms!

Esterification and Lactonization

Esterification is slow, and needs H⁺ as a catalyst. Lactonization is fast, and needs no catalyst. Can we explain this using the above?

We sure can!

Both reactions involve the formation of a new C-O bond via -OH nucleophilic attack, so they have very similar ΔH^‡ values (as the ΔH^‡ is made up of the enthalpies of bond making and breaking). This means that the difference in E_act is down to the ΔS^‡ component.

The transition state for esterification has the two reagents in specific orientation to one another. This gives the transition state many fewer translational and rotational degrees of freedom, meaning it has lower entropy and so a negative ΔS^‡. The transition state for lactonization has less specific geometric requirements in order for it to occur as it is intramolecular. The transition state's geometry is more restricted than that of the starting material, so ΔS^‡ is negative, but only quite small, as the T.S. is not very much more ordered than the reactant. By contrast, the T.S. for esterification is very much more ordered than the reactants.

Using kinetics to guess at mechanisms

Experimental rate laws can support a mechanistic guess, but not prove it. For example, if a rate law includes only reactant A, and not reactant B, we know that reactant B is not involved in the rate determining step. In addition, if a rate law is first order with respect to a reactant, we know that only one molecule of that reactant is involved in the rate determining step.

This can get more complicated when there are reactions with several slow steps. For this we use the steady state approximation.

Rate laws derived using the steady state approximation can often be simplified further using knowledge of the relative rates of each step in the reaction. If the first step of a reaction is slow and the second step is fast, k₂>>k₁. This information can be used to simplify the rate law.

Summary

In this lecture we:

Revised a little thermodynamics
Used these principles to explain how the entropy of a transition state relates to the activation energy, and so to the rate of a reaction
Revised a little kinetics

Lecture 2

The substituent constant, σ

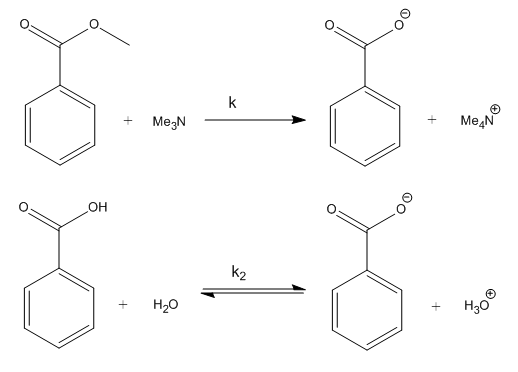
Hammett discovered that the rate of aminolysis of substituted benzoic acids was almost directly proportional to the rate of dissociation of that substituted benzoic acid.

Plotting logK(ester) against logK2(acid) resulted in an almost straight line! If we refer back to the Arrhenius equation, we can see that this means that there is a relationship between the two activation energies, and so the ΔG^‡, free energy of activation. This is called a Linear Free Energy Relationship (LFER):

$l o g k (e s t e r) = ρ l o g k 2 (a c i d) + c$

If we subtract this relationship for the unsubstituted ester and acid from that of the substituted ester and acid, we obtain this:

$l o g k (s u b e s t e r) - l o g k (e s t e r) = ρ (l o g k 2 (s u b a c i d) - l o g k 2 (a c i d))$

or:

$l o g \frac{k (s u b e s t e r)}{k (e s t e r)} = ρ l o g \frac{k 2 (s u b a c i d)}{k 2 (a c i d)}$

This equation made Hammett go 'aha!' He decided to define a substituent constant (σ) for each meta or para substituent based on the dissociation constants in water at 25^oC:

$ρ σ (s u b) = l o g \frac{k 2 (s u b a c i d)}{k 2 (a c i d)} = p K_{a} (a c i d) - p K_{a} (s u b a c i d)$

Clear?

Good.

The σ of a substituent is usually different depending on whether it is in the meta or para position. Electron donating substituents have negative values. They decrease the acidity of the acid, and increase the pK_a. Electron withdrawing substituents have positive values. They increase the acidity of the acid, and decrease the pK_a.

The reaction constant, ρ

The ρ is called the reaction constant, and is the gradient of the line in a Hammett plot. A negative value means the reaction is favoured by electron donating substituents, meaning there is an increase in positive charge during r.d.s.. A positive value means that the reaction is favoured by electron withdrawing substituents, meaning there is an increase in negative charge during r.d.s.. -1 < ρ < 1 means that the reaction is not very sensitive to changes of substituent. -1 > ρ or 1 < ρ means that the reaction is sensitive to changes of substituent.

Factors determining σ

The inductive effect is the movement of electron density along the sigma bond joining the substituent to the benzene ring. The further the substituent is from the reaction centre, the weaker this effect is.

Some substituents also have a resonance effect. The resonance effects have the greatest influence if the reaction centre is ortho or para to the substituent.

Considering only meta and para substituents, we can express each σ value as a sum of each of these effects.

$σ_{m} = (σ_{I} + σ_{R})_{m}$

$σ_{p} = (σ_{I} + σ_{R})_{p}$

Adjusted versions of the substituent constant have been calculated to take account of the conjugation (resonance effect) that occurs between para substituents and other groups on the ring. Where an electron donating group is para to another electron rich group, σ^-_p is used, and where an electron poor group is para to another electron poor site, σ⁺_p is used.

Non-liner Hammett plots

Hammett plots don't have to be straight, and this can tell you a lot about the mechanisms involved. If the line fluctuates, this can be evidence of neighbouring-group participation. If the line bends up, this means there is a change in the mechanism (from a mechanism favoured by electron donating groups, i.e. producing positive charge to one favoured by electron withdrawing groups, i.e. producing negative charge in rds). If the line bends down, it means that the rds within the mechanism has changed, i.e. a new transition state is now the rate determining one.

Summary

We have learnt:

The substituent constant, σ, shows whether the substituent increases the pK_a (negative value, reducing acidity, is electron donating) or decreases the pK_a (positive value, increases acidity, is electron withdrawing.
The substituent constant for a para substituent is modified to take into account the extra resonance effect if an EWG is para to another EWG, and the same with EDG para to EDG.
The reaction constant, ρ, is the gradient of a Hammett plot. It shows whether the rate determining step of a reaction creates negative charge in the molecule (positive value, favoured by electron withdrawing substituents) or creates positive charge in the molecule (negative value, favoured by electron donating substituents).
The Hammett plot doesn't have to be a straight line. Neighbouring group effects can make it wibble, and sometimes it can change direction entirely.
A Hammett plot bending up means that the mechanism has changed.
A Hammett plot bending down means that the rds has changed.

Lecture 3

A Recap of Acids and Bases

As I'm sure we all remember, there are two sets of definitions of acids and bases:

{ class="wikitable" |- !! Lewis !! Bronsted |- !! Acid !! Base !! Acid !! Base |- | Electron acceptor || Electron donor || Proton donor || Proton acceptor |}

The strength of a Bronsted acid is how well it donates a proton to a Bronsted base. Water is used as the conjugate base, and the equilibrium constant of this is the K_a. The -logK_a is the pK_a. We can use the pK_a to calculate the position of equilibrium. Equilibrium will always be driven towards the side with the higher pK_a. The equilibrium constant of a reaction, K_eq can be calculated from the pK_a of the right hand acid and the left hand acid, thus:

$K_{e} q = p K_{a} (r h a) - p K_{a} (l h a)$

pK_a is more complex than we supposed

The problem is that the pK_a is calculated in aqueous solution, and most reactions are done in organic solvents. There are adjusted pK_a values available for each reagent/solvent combination. This means that the position of equilibrium can change radically depending on the solvent used.

The dielectric constant

The dielectric constant, ε, for a solvent measures the electrostatic interactions between ions and the solvent, i.e. it is a measure of the solvent's polarity. It is defined as:

The factor by which the magntiude of the electric field surrounding a charged particle is reduced in a medium compared to the same particle in a vacuum.

The value varies with the dipole moment of the solvent molecules, the interactions between the individual bond dipoles in the molecules, and more specific intermolecular interactions, such as hydrogen bonding.

For a polar solvent, ε > 15, as a rule.

Solvent effects

The dielectric constant alone doesn't account for all the effects a solvent has on pK_a. There are also interactions between the solvent and solute molecules, which doesn't necessarily correlate with the polarity of the solvent. Organic solvents tend to be worse at solvating anions than cations, for instance.

This results in 'naked' anions, where anions are poorly solvated by polar aprotic solvents due to the weakness of their interactions. This means that anionic species are way more reactive in polar aprotic solvents than in polar protic solvents.

An example of this is the reversal of halide reactivity. In protic solvents, I^- is more reactive than F^-, as the smaller ion is more tightly solvated. In aprotic solvents, the reverse is true, and the ion with the highest charge density is the most reactive.

We can model solvents in two ways. Apolar solvents are best modelled as a dense gas. Polar solvents are modelled as a highly imperfect solid.

Generally speaking, if the transition state is more polar than the reactants, a more polar solvent with solvate it better than the reactants, lowering ΔH^ǂ and increasing the reaction rate. The reverse also applied. When there is little change in polarity between reactant and transition state, solvents are unlikely to have a large effect on rate.

Summary

In this lecture we covered:

Acids and bases recap
How relative acidities affect the position of equilibrium
The dielectric constant, and how that relates to
Relative reactivities in different solvents
The effect of all of these on rate.

Lecture 4

A Brief Recap of Thermodynamic vs. Kinetic control

If a reaction is under thermodynamic control, it is at equilibrium and the most thermodynamically stable product will predominate. If a reaction is under kinetic control, the product that forms from the lowest energy transition state will predominate. Reaction conditions can be altered to ensure that a reaction is under one kind of control or another. At low temperatures, the reaction is more likely to be under kinetic control, because few product particles have the energy necessary to return through the transition state. At high temperatures, the reaction is more likely to be under thermodynamic control because much of the product has the necessary energy to return through the transition state.

The Hammond Postulate

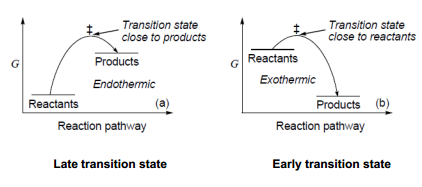
Transition states have a lifetime of essentially zero, so they can't be observed experimentally. This means that we need to approximate their structure. The Hammond postulate states that the transition state looks most like the state it is closest to in energy. This means that if the reaction is exothermic, the transition state will resemble the reactants most, and if it is endothermic, the transition state will resemble the products most. If the transition state resembles the reactants most, it is closer to them along the reaction co-ordinate, and we call it an early transition state. If the transition state resembles products most, it is closer to them along the reaction co-ordinate, and so is called a late transition state.

We can 'move' the theoretical transition state by stabilising the products or the reactants relative to the transition state. As the reactants become more stable, the transition state becomes 'later' and the same in reverse.

Isotopes in Mechanistic Studies

By 'labelling' an atom, we can see where exactly that particular atom goes (through later NMR analysis). This can help to clarify the mechanism. Through observing what effect this labelling has on the rate of the reaction, we can see which bond formations and dissolutions are in the rds.

The Primary Kinetic Isotopic Effect is where one of the bonds to the isotopically labelled atom is made or broken in the rate determining step. The extra mass of the isotope (such as when substituting deuterium for hydrogen) affects the rate quite significantly. This is because the extra mass of the isotope increases the reduced mass of the bond, so increasing the dissociation energy, and reducing the energy of the reactants. This affects the ΔH^ǂ, increasing it, and so decreasing the rate of the reaction.

How much effect the PKIE has depends on what the rate determining step of the reaction is. If there is an early transition state, the isotope-reactant bond will be largely intact, so the ΔH^ǂ will be the same as that of the non-isotope reaction, meaning that there is little effect on the rate. If there is a symmetric transition state, with the centre weakly bound to both the isotope and the incoming group, the energy of the transition state will be unaffected by the presence of the isotope, and so will be very similar to the energy of the non-isotopic transition state. This means that the activation energy barrier for the isotopically labelled reactants will be greater, and so the rate will be slower, and a PKIE will be observed. If there is a late transition state, the same argument applies as for an early transition state, so a small PKIE will be observed. The value of the PKIE is between one and a maximum, which is dependent on temperature.

Secondary kinetic isotope effects occur when the isotope has a small impact on the rate, but is not directly involved in any bond breaking or making. This can occur when the centre to which the isotope is bonded changes geometry (i.e. hybridisation), or makes or breaks a bond. The effect is typically around 1.15. They are observed particularly when sp³ hybridised centres change to sp². SKIE are observed because the stronger isotope-centre bond is shorter than the atom-centre bond, providing less steric hindrance, and so lowering the energy of observed vibrations.

Summary

In this lecture we:

Revised the ideas of thermodynamic and kinetic control
Saw that an exothermic transition state resembles the reactants more
Saw that an endothermic transition state more closely resembles the products
Learnt that the primary kinetic isotopic effect is observed most when the rds involves breaking of the isotopically marked bond.
Learnt that the secondary kinetic isotopic effect is observed most when an sp³ centre is convereted to an sp² centre.

Lecture 5

A Recap of Catalysts

Catalysts, as I'm sure we're all aware, are very important. They increase the rate of a reaction by changing the pathway by which the reaction occurs to one with a lower ΔG^ǂ. This can mean that the catalysed reaction contains many more steps than the uncatalysed reaction.

Catalysts and Kinetics

The overall rate of a catalysed reaction is (loosely) described by this expression:

$R a t e = k_{0} [R e a c t a n t] + k_{c a t} [C a t a l y s t]^{n} [R e a c t a n t]$
$R a t e = (k_{0} + k_{c a t} [C a t a l y s t]^{n}) [R e a c t a n t]$
$R a t e = k_{o b s} [R e a c t a n t]$

So by measuring the k_obs at various concentrations of catalyst, we can determine k_cat, the value of n (the number of molecules of catalyst used in the reaction), and the relative efficiency of different catalysts (by comparing k_cat values.

Acid Catalysis

When a reaction is catalysed only by H⁺ or H₃O⁺, rather than undissociated acid, we call it specific acid catalysis. Typically for these reactions, the catalysed rds is so much slower than the other reaction steps that the rate can be said to depend on the rate of the rds alone.

When a reaction is catalysed by both H⁺ and undissociated acid, it is general acid catalysis. This type of catalysis is detectable by varying the concentration of undissociated acid at constant pH and measuring the rate. If the reaction is general acid catalysed, the rate will vary. General acid catalysis is mostly important only at high pH, when the specific acid contribution is small, and the protonation is the rds. The protonation is concerted with the breaking of another bond. The strength of an acid catalyst depends on the strength of the acid.

Base Catalysis

As in the above section, there is also specific and general base catalysis. When a reaction is catalysed by OH^-, it is specific base catalysed, with a rapid deprotonation followed the the rds.

When a reaction is general base catalysed, the reactant is deprotonated by a base other than OH^-, and this is the rds. The deprotonation is concerted with the cleavage of another bond. The strength of the general base catalyst is dependent on the strength of the base.

Electrophilic Catalysis

We might well ask how this differs from acid catalysis. In general and specific acid catalysis, it is a proton that does the catalysing. In electrophilic catalysis, the catalysis is performed by a non-protic acid or a Lewis acid, such as a metal ion (Hg⁺) or a neutral Lewis acid (AlCl₃).

They can operate by bonding with the OH^- remaining when the proton of water has been attacked, by co-ordinating to a reaction centre, increasing its electrophilicity, or by co-ordinating to increase the leaving group ability of a group.

Summary

Here we covered:

A brief summary of catalysis
Specific acid catalysis is the catalysis of a reaction by H⁺ or H₃O⁺. This protonation happens quickly, reversibly and at low pH.
General acid catalysis is the catalysis of a reaction by undissociated acid. This happens slowly and at high pH.
Specific base catalysis is the catalysis of a reaction by OH^-. The deprotonation happens quickly and at high pH.
General base catalysis is when a reaction is catalysed by any other base. This happens slowly and is usually the rds.
Electrophilic catalysis is the catalysis of a reaction by an electrophile or Lewis acid. The catalysis usually occurs by abstracting the remaining OH^- from deprotonated water, co-ordinating to increase reactivity, or co-ordinating to increase leaving group ability.

3.O4 Introduction to Organic Physical Chemistry

Executive Summary

Lecture 1

A brief revision of Thermodynamics and Kinetics

Applying these to rate

SN1 and SN2

Esterification and Lactonization

Using kinetics to guess at mechanisms

Summary

Lecture 2

The substituent constant, σ

The reaction constant, ρ

Factors determining σ

Non-liner Hammett plots

Summary

Lecture 3

A Recap of Acids and Bases

pKa is more complex than we supposed

The dielectric constant

Solvent effects

Summary

Lecture 4

A Brief Recap of Thermodynamic vs. Kinetic control

The Hammond Postulate

Isotopes in Mechanistic Studies

Summary

Lecture 5

A Recap of Catalysts

Catalysts and Kinetics

Acid Catalysis

Base Catalysis

Electrophilic Catalysis

Summary

S_N1 and S_N2

pK_a is more complex than we supposed