MRD 01372542
Ng611 (talk) 19:08, 30 May 2019 (BST) Generally good. Could be improved in a number of places (see comments below). More detail and precision is needed in many of your answers (see e.g.: your answer to Q1; don't be afraid to use equations and visual aids!).
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
On a potential energy surface diagram, the reaction trajectory is defined as the path passing through the minima. To calculate this, the potential energy must be differentiated once with respect to the bond length r1 and once with respect to r2. The transition state is the point along this path at which the bond lengths are equal, and will also be the potential energy maximum of this line. To isolate this point, potential energy must be differentiated with respect to q1 and q2, the new coordinates generated from a skew plot. This will allow identification of the local maxima and minima of potential energy curve in two orthogonal axes. The second derivative of these equations can confirm whether these are maxima (-ve value) or minima (+ve value). The transition state will be the point which represents a minimum of one of these differentials, and a maximum of the other, and presents as a saddle point on the potential energy curve.
Ng611 (talk) 19:00, 30 May 2019 (BST) You should back up your explanation here with the appropriate equations.
Ng611 (talk) 19:00, 30 May 2019 (BST) What are the directions of r1 and r2 and q1 and q2? A diagram would help.
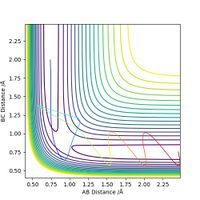
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
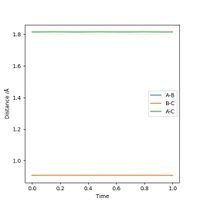
The best estimate of rts we could find is 0.9075 Å. As the transition state will be completely symmetric (by Hammond's postulate, the transition state is neither early nor late so will not resemble either the reactants or products more closely), both rab and rbc will be the same. At this point, the system has no potential energy, so no oscillations should be observed on a graph showing internuclear distance vs time. The graph for this is shown below.
Ng611 (talk) 19:01, 30 May 2019 (BST) How did you arrive at this value? Trial and error, or did you approach it more methodically?
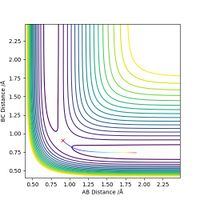
Comment on how the mep and the trajectory you just calculated differ
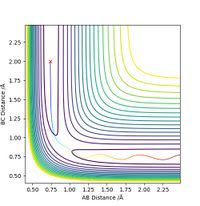
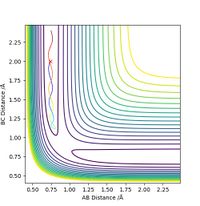
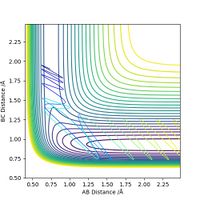
The minimum energy path will be formed just from consideration of the momentum of the bonds at every particular reaction coordinate, without consideration of previous momentum. This means that an MEP plot will not show vibrations, only the direct path leading to the transition state. The line stops at the transition state as this is the point at which the gradient is zero, and there is no momentum to consider. In the dynamic situation, the path goes beyond the transition state as there is residual momentum in the system. Residual momentum is also the reason vibrations can be seen in the dynamic approach, momentum is not set to zero at each point on the surface so any vibration occurring initially will carry through the path. In each case, the path is represented as the colour gradiated line on the contour maps below, with the red cress representing the transition state.
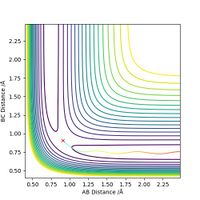
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p<sub>1</sub> | P<sub>2</sub> | E<sub>tot</sub> | Reactive? | Description of Dynamics | Illustration of the Trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Yes | Central hydrogen (B) is transferred directly between the outermost hydrogens (A, C) | 
|
| -1.5 | -2.0 | -100.456 | No | Molecule hesitates in transition state but reverts to reactants | 
|
| -1.5 | -2.5 | -98.956 | Yes | Central hydrogen is transferred directly between the outermost hydrogens | 
|
| -2.5 | -5.0 | -84.956 | No | Atom B is initially transferred from A to C, but due to large vibrations in the transition state, it reverts back to reagents | 
|
| -2.5 | -5.2 | -83.416 | Yes | Atom B is transferred initially from A to C, then vibrations around the transition state cause temporary re-association with atom A before the reaction runs to completion and transfers to C | 
|
From this table we can conclude that kinetic energy is not the deciding factor in whether or not a reaction progresses to completion. In some cases, such as the case above with momentums -2.5 and 5.0, translational energy is transferred to vibrational energy upon collision to such a degree that the H2 molecule formed can dissociate and re-form the reagents. It is also clear from the table that atom transfer is not always direct, there is often fluctuation around the transition state if a large degree of vibrational energy is present in the system.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory is comprised of three basic ideas.
1) The saddle point of a potential energy surface defines the transition state, and study of the surrounding area gives information on the rates of reaction.
2) The activated complex (transition state) is in a quasi-equilibrium (the system only deviates from equilibrium an infinitesimal amount)
3) Once the transition state is reached, the activated complex will fall over the barrier to reaction and form the products
In the results above, not all of the simulations predicted by the model follow these assumptions, so rate predictions will likely not be accurate in all cases. In the first three reactions, all of the transition state theory assumptions are true, so any theoretical prediction of rate will likely be representative of reality. The fourth reaction differs from the transition state assumptions as the activated complex does not fall directly into the products once the quasi-equilibrium is reached, it fluctuates about the transition state and reforms the reactants. A similar situation is observed in the fifth reaction, in which the central proton is transferred between the outermost hydrogens multiple times before forming the products, so the molecule passes through the transition state multiple times. For these final two cases, theoretical predictions of rates are unlikely to match what is observed.
Ng611 (talk) 19:03, 30 May 2019 (BST) Will TS theory therefore overestimate or underestimate the reaction rate?
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
It can be seen from the potential energy graphs below that whilst not all reactions ran to form the products under specified conditions, the curve shows the thermodynamics of the process. In the reaction of H-H with a fluorine atom, the potential energy minimum of the product (H-F) can be seen as much lower than the starting material, showing that the reaction is exothermic. In the reverse reaction, again it did not run to completion as shown by the black path line, but the energy difference between products and reactants shows that the conversion of H-F to H-H is an endothermic process.
Relating this back to bond strength, this shows that the HF bond is much stronger (due to an ionic contribution to the bond, strengthening it), as it is lower in energy, and formation of it results in the loss of excess energy as thermal energy.
Locate the approximate position of the transition state.
The best estimate of the transition state for the reaction of H2 with F has r1=1.8108 Å and r2=0.74493 Å. This was obtained through observation of the mep, and zooming in on the coordinates of the final position. These were then entered as the starting conditions with no momentum, and on a dynamic plot of internuclear distance vs time, no movement can be seen for any atm. This confirms that this is nearly, the transition state (there is some force present between the atoms looking at the analysis so it is not the exact state but has been minimised to the largest extent it can be).
Report the activation energy for both reactions.
The activation energy for both reactions was found by looking at the energy vs time graph around the point of the transition state, and observing the change in total energy from reactants to products. The activation energy of the first reaction (H2 + F) was found to be 30.2 kcalmol-1. This is the larger of the two energies. The activation energy of the second reaction (FH + H)was observed as 0.0094 kcalmol-1.
Ng611 (talk) 19:04, 30 May 2019 (BST) Your Ea for the FH+H reaction is a little off, but you've got the general trend correct. Well done!
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally
The initial conditions found that result in a
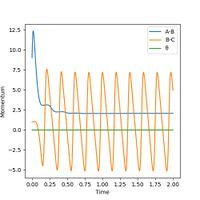
Upon proton transfer, the vibrational energy present in the H-H bond is transferred to the vibrational energy in the H-F bond. This will increase the momentum of HF and decrease that of HH, as shown in the graph below. The program can confirm that energy is conserved by looking at the energy vs time graph, as potential end kinetic energy exactly mirror each other as the molecules vibrate and interact< In the end, the H atom poseses only translational energy whilst the HF molecule contains both vibratinal and translational energy.
This could be confirmed experimentally by running
Ng611 (talk) 19:05, 30 May 2019 (BST) Think you meant to finish this sentence later. Or did you literally mean that running a marathon would magically confirm your hypothesis to you?
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
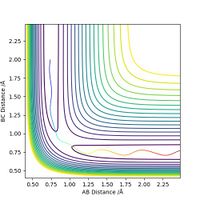
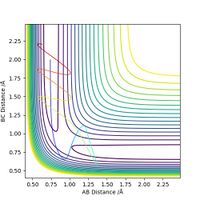
When adding more momentum into the system, this will not always result in an increased likelihood of traversing the transition state and forming the products, despite the overall increase in energy of thee system. The two contour plots below have the exact same initial conditions bar the momentum of AB, which is -1 in the case on the left and -2.5 on the case on the right. The right hand side has a greater energy input but does not run to completion. So much energy has been put into the H2 vibration that once the saddle point has been traversed, it can overcome the reverse reaction activation energy and does not form the products.
Polanyi's rules state that a molecules vibrational state is unlikely to influence the reaction rate to a significant degree, but only if the reaction has an early transition state. The reaction above has an early transition state, as it more closely resembles the products than the reactants. The fact that it disputes the empirical rules suggests that the rule may not apply to all conditions, especially in very high vibrational states.
If conditions are set up for the reverse reaction, a very hihg momentum of HF is required to achieve a reactive trajectory. These conditions show swift transfer of FH vibrational energy to H2 translational energy. Once the transition state has been overcome, the hydrogen molecule has enough translational energy to increase the intermolecular spacing to such a degree that further vibration will not induce the reverse reaction and reform the products.
Ng611 (talk) 19:06, 30 May 2019 (BST) Good!
From this it can be concluded that high vibrational nodes, whilst sometimes useful to find a reactive trajectory, are inefficient in terms of the reaction. The energy input will far exceed that of the activation energy, to no observabale advantage. This inefficiency is observed with greater frequency in systems with a late transition state, as the activation energy of the reverse reaction is smaller, meaning a smaller vibrational energy excess is needed to reform the products. This means that a larger proportion of reaction trajectories will fail to be successful in forming the products, reducing efficiency.