MRD:zz161701327485
Exercise 1
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
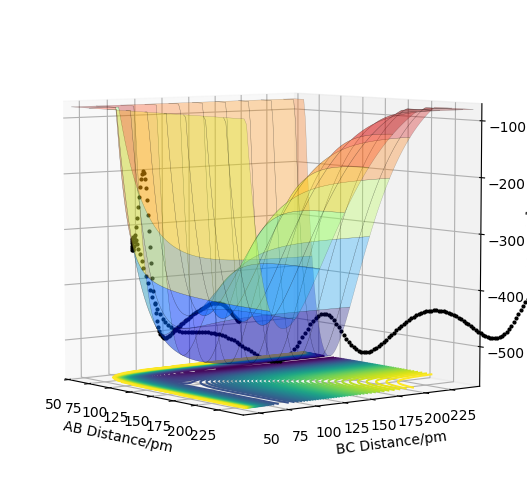
The transition state is mathematically defined as the point that the gradient of the potential equals to zero. It can be expressed as ri where ∂ V(ri)/∂ ri=0. On a potential energy surface diagram, the transition state is identified as the saddle part of the minimum energy path. In the diagram below, the transition state is where on the minimum energy path (the black line) AB = 0.75-1.00 and BC = 1.00-1.25. The transition state is not only a local minimum of the potential energy surface but where the energy goes down most steeply along the minimum energy path linking reactants and products. (The definition is ok but you need to say second partial derivative. Besides, pay more attention on how you describe this concept.) Cq3417 (talk) 15:35, 15 May 2019 (BST)
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with an “Internuclear Distances vs Time” plot for a relevant trajectory.
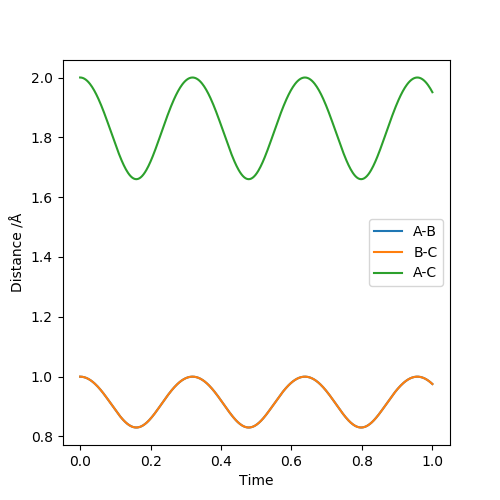
In the plot below, it is set that r1=r1=1, p1=p2=0. The best estimate of the transition state position is where AC is minimum, where T = 0.156 or 0.473 or 0.797, AC = 1.654, rts= AB = BC = 0.825. This is the transition point because the gradient of the potential is zero at the point (local minimum of the potential energy surface), and AC reaches the minimum which means the greatest probability of interactions among A, B and C.
(Seems that your system didn't reach the transition state and I think you can report better result.) Cq3417 (talk) 15:35, 15 May 2019 (BST)
Comment on how the mep and the trajectory you just calculated differ.

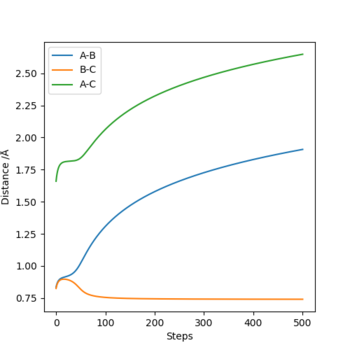
For the mep, atom C almost always keeps a same distance (around 0.75) from atom B, while atom deviates from atom B quickly with an increasing speed. This shows that BC becomes a molecule after the transition state. Foe (for) the trajectory, A-B and B-C keep almost the same distance until T=0.6, and later B-C vibrates more greatly than A-B. In this case, it is not clear to see which two atoms become a molecule. The three atoms are reasonably close to each other at all times. (I think you can describe more about how vibration affects the difference.) Cq3417 (talk) 15:35, 15 May 2019 (BST)
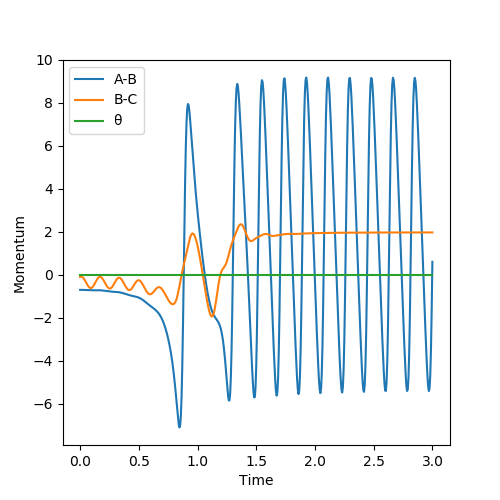
Look at the “Internuclear Distances vs Time” and “Momenta vs Time”. Take note of the final values of the positions r1(t) r2(t) and the average momenta p1(t) p2(t) at large t. What would change if we used the initial conditions r1 = rts and r2 = rts+0.01 instead? Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?
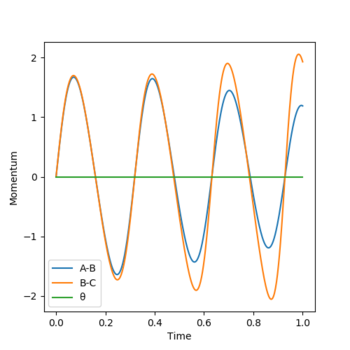
In the trajectory mode, the final value of r1 = 1.00, r2 = 0.88. Both of the average momenta at large t equals to zero. If we used the initial conditions r'1 = rts and r'2 = rts+0.01 instead, the graph of r'1(t) and r'2(t) would interconvert, where r'1(t) = r2(t), r'2(t) = r1(t), p'1(t) = p2(t) and p'2(t) = p1(t).
(You confused me.) Cq3417 (talk) 15:35, 15 May 2019 (BST)
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
| p1 | p2 | Etot | Reactive? | Description of the dynamics |
|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Reactive | Molecule AB (with weak vibration) and atom C moves close to each other, BC becomes a molecule and moves away from C, molecule BC vibrates weakly |
| -1.5 | -2.0 | -100.456 | Unreactive | Molecule AB (with weak vibration) and atom C moves close to each other, and moves away; molecule AB vibrates weakly |
| -1.5 | -2.5 | -98.956 | Reactive | Molecule AB and atom C moves close to each other, BC becomes a molecule and moves away from C, where atom A has a greater speed than BC, molecule BC vibrates weakly |
| -2.5 | -5.0 | -84.956 | Unreactive | Molecule AB and atom C moves close to each other, BC gets closer to each other (with great vibration) shortly, then AB becomes a molecule (with great vibration) again and moves away from C |
| -2.5 | -5.2 | -83.416 | Reactive | Molecule AB and atom C moves close to each other, then BC gets closer (with great vibration) shortly, then AB gets closer (with great vibration) again shortly. After a long transition state, BC finally becomes a molecule (with great vibration) |
From the table above, we can conclude that the reaction is reactive when there is a relatively large difference between p1 and p2, otherwise, the reaction is unreactive. When p1 and p2 are relatively low (more negative), they will experience a longer transition state, and molecules would vibrate more strongly.
(I think you need to emphasise the role of transition state here.) Cq3417 (talk) 15:35, 15 May 2019 (BST)


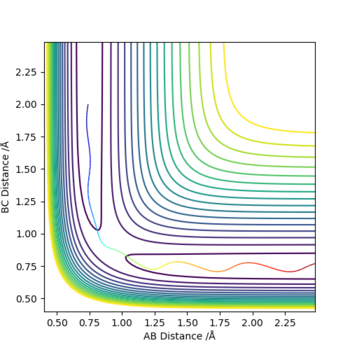

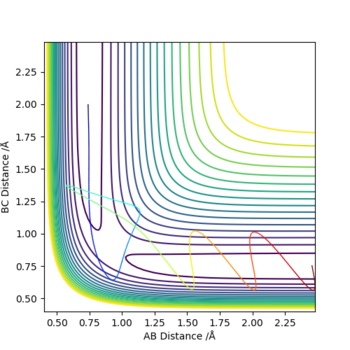
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The main assumptions of Transition State Theory are: Transition state is defined as the saddle point of the potential energy surface. The activated complexes would reach quasi-equilibrium with reactants and could be converted to products. [1]
From the experimental results, we can confirm that all reactive reactions have a transition state. Unreactive reactions may have a transition state (4th example, p1=-2.5, p2=-5.0) and may not have a transition state (2nd example, p1=-1.5, p2=-2.0). In the 4th example, the activated complexes are in equilibrium with the reactant molecules but did not convert into products.
(You need to discuss this in detail and show your understanding of this topic.) Cq3417 (talk) 15:35, 15 May 2019 (BST)
Exercise 2
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state. Report the activation energy for both reactions.
F + H2 is an exothermic reaction, and H + HF is an endothermic reaction. This is reasonable because H-H bond energy is 432 KJ/mol, and H-F bond energy is 565 KJ/mol [2]. Therefore, it requires more energy to break an H-F bond than forming an H-H bond, vice versa. The approximate position of the transition state of H+HF is AB=3.45, BC=0.92. The approximate position of the transition state of F+H2 is AB=1.82, BC=0.74. The activation energy of H+HF is 29, and the activation energy of F+H2 is 0.2.
(Again, detail please.) Cq3417 (talk) 15:35, 15 May 2019 (BST)

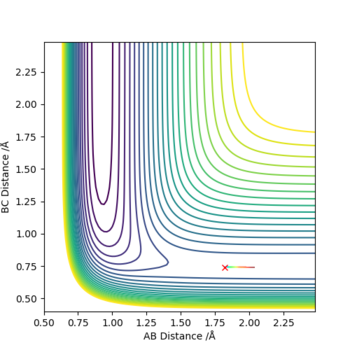

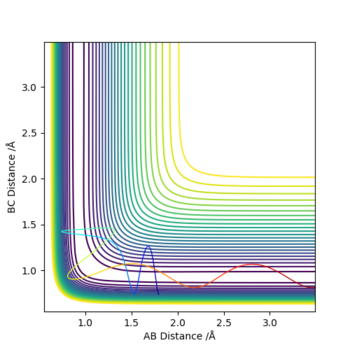
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
When r(HF)=1.82, r(HH)=0.74, p(F)=-0.7, p(HH)=-0.1, the reaction could exactly happens.
For exothermic reactions, some energy in the system will be transformed to heat and release to the surroundings. Experimentally, this can be observed by rise of temperature of the surroundings and decrease of temperature of the system.
For endothermic reactions, the system would absorb energy from the surroundings. Experimentally, this can be observed by decrease of temperature of the surroundings and rise of temperature of the system.
F+H2 is an exothermic reaction. So experimentally, decrease of temperature of the surroundings and rise of temperature of the system should be observed. From the graph above, we can see that the new molecule F-H vibrates greatly.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's empirical rules state that vibrational energy is more efficient than translational energy in activating a late-barrier reaction, but the reverse is true for an early-barrier reaction [3].
Experimentally, for reaction F+H2, where r(HH)=0.74, p(FH)=-0.5, when p(HH) is less than 1.76, the reaction could happen, and otherwise it cannot happen. F+H2 is an exothermic reaction and is a early-barrier reaction. From the graph, we can see that the reactions happens when there is more translational energy than vibrational energy.
Experimentally, H+HF is an endothermic reaction and is a late-barrier reaction. From the graph, we can see that the reactions happens when there is more vibrational energy than translational energy.
Therefore, Polanyi's empirical rules can be proved by the experiments.



(Overall, this report can be improved by describing more detials.) Cq3417 (talk) 15:35, 15 May 2019 (BST)
References
[1]D. M. Hirst Potential Energy Surfaces: Molecular Structure and Reaction Dynamics Taylor and Francis, 1985
[2]Chemical Bond Energies: http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html
[3] Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim: Dynamics of the Reaction of Methane with Chlorine Atom on an Accurate Potential Energy Surface, 2011