MRD:zy1416

EXERCISE 1: H + H₂ system

Question 1: What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The gradients of r₂ in the potential energy surface at one minimum is zero and the gradient of r₁ in another minimum is zero.

The curvatures of both components of the potential energy surface for minima are positive. i.e the second derivative ∂²V(r1)/∂(r1)² => 0 ∂²V(r2)/∂(r2)² => 0

At the transition state, the gradients for both components are both zero. But one of the curvatures is negative and one of the curvatures is positive.

Mm10114 (talk) 23:39, 28 May 2018 (BST) This is a good attempt. However, if you describe a specific potential energy surface (you use "r1" and "r2") it would require a figure. About the transition state, which curvature is negative, which positive? From your answer I cannot tell, and what about the values of second partial derivatives?

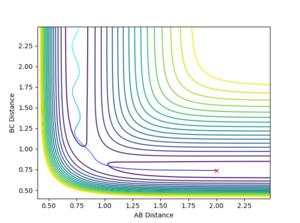
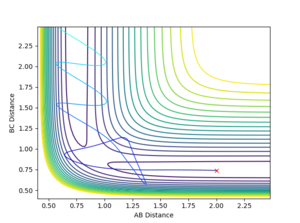
Question 2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

• The transition state position is estimated at r1=r2= 0.908 Å. The “Internuclear Distances vs Time” plot shows two almost flat lines, indicating that the atoms hardly oscillates and are close to an equilibrium. The distance of AB equals to the distance of BC so the two lines overlap.

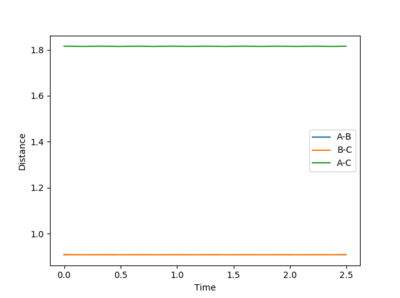
Mm10114 (talk) 23:39, 28 May 2018 (BST) Overall good. But, it would be helpful if you briefly described the process how you have obtained the r1=r2= 0.908 Å value. Just reporting the numerical value is not enough. You have to show/describe the whole process.

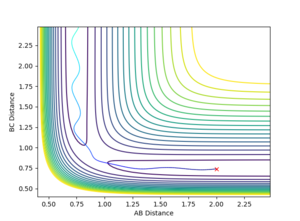
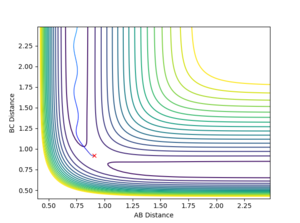
Question 3: Comment on how the mep and the trajectory you just calculated differ.

• The MEP trajectory reflects the reaction trajectory of the dynamics trajectory but occurs at longer time. The momentum of the MEP trajectory is always zero because the velocity is reset to zero in each time step. Therefore the MEP trajectory is smooth.

Mm10114 (talk) 23:39, 28 May 2018 (BST) A good attempt. However, this answer is a little bit scarce. I get what you mean at the beginning, but why MEP requires longer time? Explain. The second part is also correct but lacks a final conclusion. It is smooth why exactly? Some more in-depth analysis and explanation of the difference is needed here.

• Final values of the positions r1(t) r2(t) and the average momenta p1(t) p2(t) at large t :

(500 steps for the dynamics calculation and 100000 steps for the MEP calculation)

	r1 = rts+δ, r2 = rts		r1 = rts+δ, r2 = rts
	MEP	Dynamics	MEP	Dynamics
r1	1.72	8.99	0.74	0.74
r2	0.75	0.74	1.75	8.93
p1	0	1.24	0	2.48
p2	0	2.47	0	1.26

• With the initial conditions of r₁ = r_ts+δ, r₂ = r_ts, the r₂ values under MEP and dynamics calculations eventually convergence as the H-H bond length is 0.74 Å. The r₁ differs because the two trajectories end at different points after the formation of the H-H molecule, in which the hydrogen atom formed is at different positions.

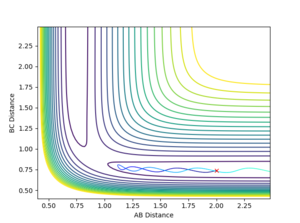
Question 4: Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

p1	p2	total energy / kcal mol-1	reactivity	plot	description
-1.25	-2.5	-99.-018	reactive		trajectory crosses the TS and moves towards the product; r2 decreases in the entrance channel and r1 does not fluctuate; trajectory shows vibration in r2 as r1 increases in the exit channel
-1.5	-2.0	-100.456	unreactive		trajectory does not reach the transition state and moves back towards the initial point in the entrance channel; shows vibration in r1
-1.5	-2.5	-98.956	reactive		trajectory crosses the TS and moves towards the product; slight vibration in r1 as r2 decreases in the entrance channel; vibration in r2 as r1 increases in the exit channel
-2.5	-5.0	-84.956	unreactive		trajectory crosses the transition state region but reverts back to the reactants
-2.5	-5.2	-83.416	reactive		trajectory crosses the transition state and reverts back to the entrance channel and eventually moves towards the products

Mm10114 (talk) 23:39, 28 May 2018 (BST) Overall ok. You have a typo in the first total energy. Also, for the 4th and 5th case, what is the appropriate term for this TS 'crossing' forth and backwards mechanism? Some additional reading would be helpful. Also, from the perspective of the initial momenta in 4th and 5th case, in comparison with 1-3, what conclusions could be made?

Question 5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

• There are three main assumptions made in the transition state theory:[1]

1.The quantum-tunneling effects and the Born-Oppenheimer approximation are ignored.

2.The atoms in the reactant state have energies that are Boltzmann distributed.

3.At the transition state, with a velocity towards the product configuration, it will not re-enter the initial state region again.

• The limitation of the transition state theory is that the quantum-tunneling effect is assumed to be negligible. However, quantum mechanics shows that particles can tunnel through the energy barrier created by the transition state, allowing the reaction to occur. So the experimental values of the reaction rate would be higher than the theoretical values.

Mm10114 (talk) 23:39, 28 May 2018 (BST) That is correct. However, you only mention tunneling. What about the second and third postulates? Especially the third in relation to the previous exercise where in 4th and 5th case you observe TS re-crossing?

EXERCISE 2: F - H - H system

PES inspection

Question 6: Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

• H + HF :

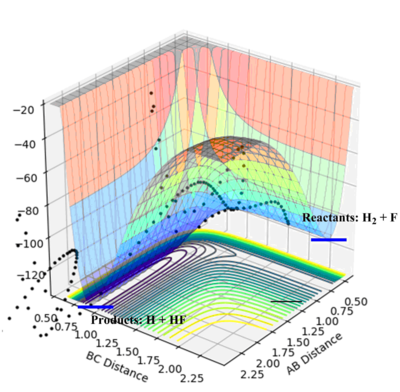
It can be seen from the PES plot of this reaction that the products have higher energy than the reactants, indicating an endothermic reaction. H-F bond is strongly polarisd and has a large ionic component with strong bond strength. The energy required for breaking the H-F bond can not be compensated by the energy gain from the formation of a H-H bond. So overall the reaction is endothermic.

• F + H₂:

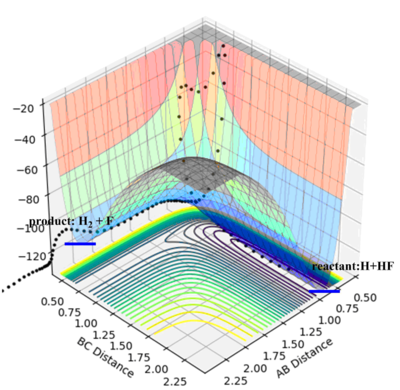
The PES plot of F + H₂ shows that the reactants have higher energy than the products. This reaction is exothermic. As discussed above, the formation of H-F bond would gain a large enthalpy due to strong bond strength and this energy gain compensates the energy lose for breaking the H-H bond. The overall reaction is exothermic.

Question 7: Locate the approximate position of the transition state.

• For H+HF, the reaction is endothermic and the transition state would resemble the product; for the other reaction which is exothermic, the transition state would resemble the reactants which is the products for the first reaction. These two reactions would have the same transition state H--H--F. And the approximate position can be located on the PES plot.

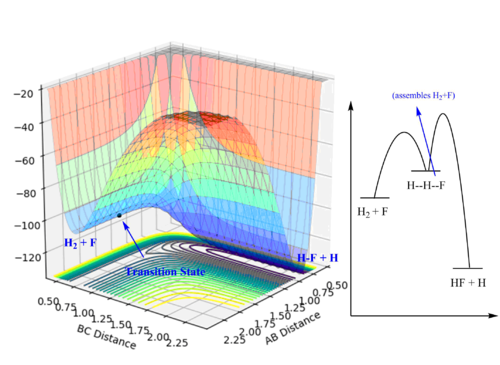
• The distance between H and H is determined to be 0.745 Å and the distance between H and F is determined to be 1.810 Å. The “Internuclear Distances vs Time” plot confirmed this position. The activation energy for the endothermic reaction is much higher than the exothermic reaction. Because the transition state resembles the H₂+F species and they have similar energies.

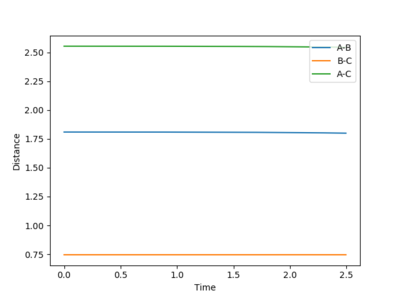
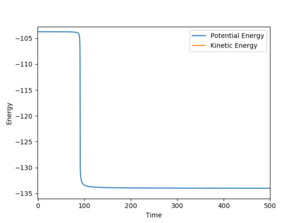
Question 8: Report the activation energy for both reactions.

H+HF	H2+F
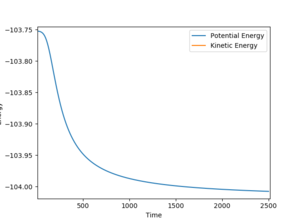Ea = (-103.785)-(-134.016) = 30.231 kcal/mol	Ea = (-103.752)-(-104.007) = 0.255 kcal/mol

Mm10114 (talk) 23:41, 28 May 2018 (BST) I can see you've obtained the values from these plots, however, an explanation in form of 1-2 sentences would be nice. You need to show an understanding of what you're doing and help me follow your reasoning.

Reaction Dynamics

Question 9: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The initial conditions have been set to be r_H-H=0.74 Å , r_H-F=2.00 Å and momentum_H-F=-10. The potential energy released is converted into the kinetic energy of the hydrogen atom. It can be seen from the Momenta vs Time plot that p_HH increases after the collision. The kinetic energy would be further convert into thermal energy as the product hydrogen atoms collide with each other. There would be an temperature increase for this exothermic reaction which can be measured experimentally.

Questin 10: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

• F+H₂

With a small momentum of -0.5 for the coming H atom, the reaction would be mostly unsuccessful even the H-H bond has a vibration energy which is significantly larger than the activation energy (0.255 kcal/mol) except for a few values of momenta such as +2.6 and -2.4. The feasibility of the reaction is not solely dependent on the energy distribution, but might also rely on the proceeding of the trajectory which would be very sensitive to specific conditions.

pHH	Contour Plot	pHH	Contour Plot	pHH	Contour Plot	pHH	! Contour Plot
-3.0		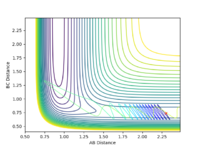-2.9		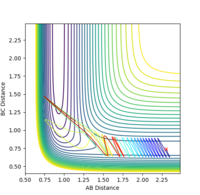-2.0		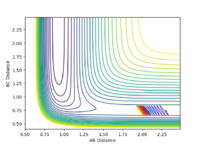-2.4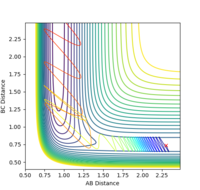
-1.0		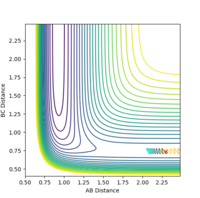0.0		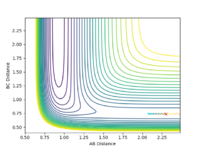1.0		2.6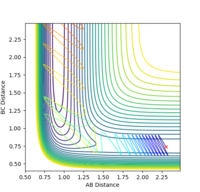
2.0		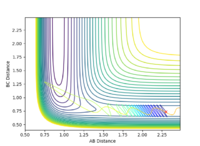2.9		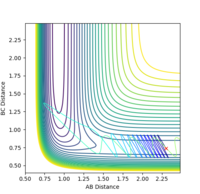3.0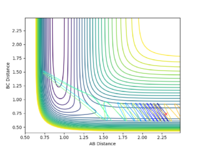

When the momentum p_FH is increased slightly from -0.5 to -0.8 with p_HH being only 0.1, the reaction now becomes successful. It indicates that the F-H vibration energy has a larger contribution for the feasibility of this reaction compared to the translational energy which is the kinetic energy of the hydrogen atom which is defined by the momentum p_HH

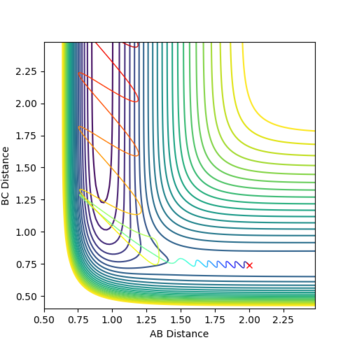
• H+HF

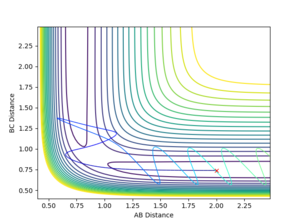
When the p_HH has a large value above the activation energy (30.231 kcal/mol), which was set to be -20. The hydrogen atom collides with the HF molecule and breaks the H-F bond. However, two hydrogen atoms moves apart and do not form a H₂ molecule. The procedure described is illustrated in the following animation snapshots. After the collision, the large momentum that the reactant hydrogen atom contains is still large.As a result, even if an H-H bond can be formed, it would immediately be broken due to an excess vibrational energy between two atoms.

One reactive trajectory has the conditions of r_FH = 0.91 Å, r_HH = 2.0 Å, p_HF = -0.5 and p_HH = -10. The trajectory recrosses the transition state region twice and eventually moves into exit channel, forming products. By comparing this condition to the initial condition, the momentum p_HH, which is the translational kinetic energy of the H atom, is reduced by a half; and the p_HF, the vibrational energy of the H-F bond is increased to -0.5. This indicates that the vibrational energy has a greater contribution to the feasibility of the reaction than the translational energy. This is the opposite situation of the H₂+F reaction.

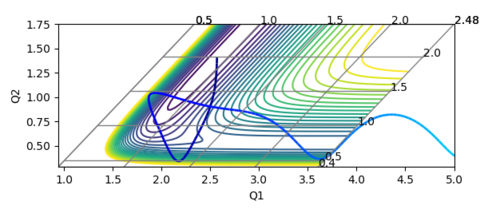
• Conclusion: The results agree with the Polanyi's empirical rules[2], which state that the vibrational energy is more efficient in promoting late-transition-state reactions and the translational energy is more efficient in promoting early-transition-state reactions.

Mm10114 (talk) 23:44, 28 May 2018 (BST) This section is really nice. You make good observations, relate to the Polanyi's rules (and reference them).

Reference

1.Zhang, Z., Zhou, Y., Zhang, D., Czakó, G. & Bowman, J. Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD 3 Reaction. The Journal of Physical Chemistry Letters 3, 3416-3419 (2012).

2.Bligaard, T. & Nørskov, J. Heterogeneous Catalysis. Chemical Bonding at Surfaces and Interfaces 255-321 (2008). doi:10.1016/b978-044452837-7.50005-8