MRD:zwl115
1. What value does the total gradient of the potential energy surface have at a minimum and at a transition structure?
The gradients at the minimum and at the transition state are the same and are both 0.
Briefly explain how minima and transition states can be distinguished using the curvature of the potential energy surface.
For the minima, the second derivative is positive. For the transition state, the second derivative can be positive or negative depending on the direction and it is the maximum of the minimum energy path of the potential energy surface.
I see what you mean. But you need to be more precise using terms like second partial derivatives, not just THE second derivative. Je714 (talk) 14:49, 31 May 2017 (BST)
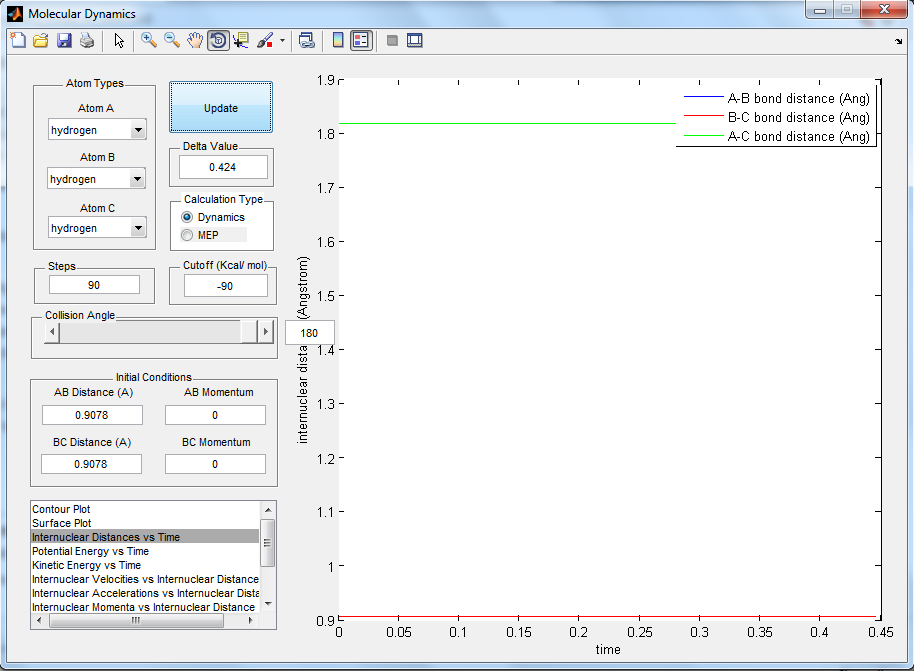
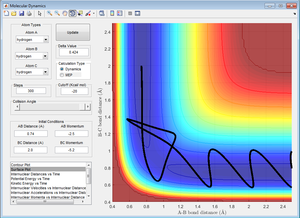
2. Report your best estimate of the transition state position and explain your reasoning illustrating it with a 'Internuclear Distances vs Time' screenshot for a relevant trajectory
The best estimate of the transition state position is 0.9078 Å between the H atoms. At this position, the internuclear distances does not change over time. If the intial position is at the transition state and there is no initial momentum, it will remain there forever. Hence, if the initial position is at the transition state, the internuclear distances will not change over time.
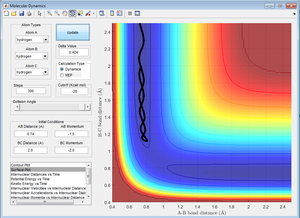
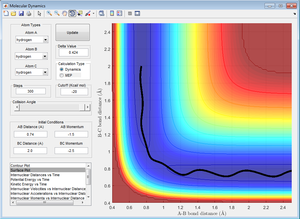
3. Comment on how the mep and the trajectory calculated using Dynamics differ.
The trajectory calculated using the mep follows the valley floor as a straight line whereas the trajectory calculated using dynamics follows a wavy line. That's just a simple observation. We're looking for more in-depth explanation here. Why is this so? What's the MEP calculation doing differently than an MD simulation? Have you looked at what the Kinetic Energy is over time for the MEP calculation? What does that tell you about the velocities? Je714 (talk) 14:49, 31 May 2017 (BST)
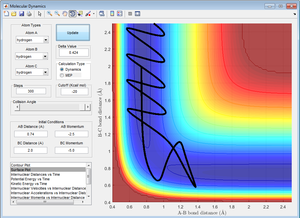
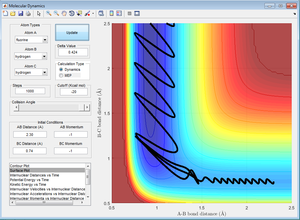
4. Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of intial conditions, provide a screenshot of the trajectory and a small description of what happens in the trajectory.
| p1 | p2 | Trajectory | Description |
|---|---|---|---|
| -1.25 | -2.5 |  |
As C approaches molecule A-B, the distance between B and C decreases while the distance between A and B remains constant. They have sufficient momenta and kinetic energy to overcome the activation barrier, hence the trajectory passes through the transition state. Past the transition state, A moves away from the new molecule B-C. |
| -1.5 | -2.0 |  |
As C approaches molecule A-B, the distance between B and C decreases while the distance between A and B oscillates due to the molecule's vibrational energy. With the decrease in initial values of p1 and p2 from the first run, the reactants have insufficient momenta and kinetic energy to overcome the activation barrier, hence the unreactive trajectory bounces off the barrier and regenerates the reactants, A-B and C. |
| -1.5 | -2.5 |  |
As C approaches molecule A-B, the distance between B and C decreases while the distance between A and B oscillates slightly due to the molecule's vibrational energy. With an increase in the intial value of p2, this increases the vibrational energy of the hydrogen molecule and the reactants now have sufficient momenta and kinetic energy to overcome the activation barrier, hence the reactive trajectory passes through the transition state and forms the products as the distances between C and B oscillates slightly due to its vibrational energy while A moves away from the new molecule, B-C, formed. |
| -2.5 | -5.0 |  |
As C approaches molecule A-B, the distance between B and C decreases while the distance between A and B remains relatively constant due to vibrational energy. They have sufficient momenta and kinetic energy to reach the transition state, but does not pass through the transition state and momentarily forms the products. However, A and C both move away from B for a brief moment, before C approaches B while A continues to move away from B. A finally approaches B-C again and C moves away from the molecule A-B, regenerating the reactants again. Therefore, the trajectory is unreactive. Hence, even though the reactants had sufficient kinetic energy to reach the transition state, the reaction was not reactive. This illustrates the importance of the reactants having the right balance of vibrational and translational energy and that reaching the transition state does not mean the reaction is going to be reactive. |
| -2.5 | -5.2 |  |
As C approaches molecule A-B, the distance between B and C decreases while the distance between A and B remains constant. They do not pass through the transition state even though they have sufficient kinetic energy and momentarily regenerates the reactants. However, the reactants still have sufficient kinetic energy and approach again to form the products as the distances between C and B oscillates strongly due to its large vibrational energy while A moves away from the new molecule, B-C, formed, without passing directly through the transition state which illustrates that the reaction trajectory does not have to pass through the transition state directly for the reaction to be reactive. |
5. State what are the main assumptions of the Transition State Theory. Given the results you have obtained, how will Transition state Theory predictions for reaction rate values compare with experimental values.
According to collision theory, if the reactants have sufficient energy and collide at a particular orientation, and the transition state theory states that this will lead to the formation of an activated complex at the transition state. Once the activated complex is formed, transition state theory states that it is in equilibrium with the reactants and the products. This transition state occurs at the lowest energy saddle point on the potential energy surface. Hence, successful reactions occur when reactants have sufficient energy to overcome the activation barrier and pass through the transition state before forming the products. This can be seen from the first 3 results obtained in part 4, where only reactions which had sufficient energy reached the transition state and are reactive.
However, based on the results obtained from runs 4 and 5, this is not always the case. For example, from the table in part 4, when p1 = -2.5 and p2 = -5.2, the reaction trajectory is reactive even though it does not pass through the lowest energy saddle point on the potential energy surface (transition state). Hence, this shows that when molecules have more momenta and occupy higher energy vibrational modes, the collisions for the reactants may not pass through the lowest energy saddle point (transition state), but the reaction trajectory is still reactive and the products are formed. Furthermore, when p1 = -2.5 and p2 = -5.0, even though the molecule had enough energy to reach the transition state, due to its higher vibrational and translational energy, its motion is more complex and its reaction trajectory does not pass through the transition state and is unreactive. Thus, this assumption for the transition state theory may not be applicable when temperatures are high as molecules will have higher vibrational energy as reaction rates are not dependent solely on the transition state.
This is called re-crossing of the TS Je714 (talk) 14:49, 31 May 2017 (BST)
The Transition state theory also assumes classical mechanics such that only reactants which collide with sufficient energy are able to overcome the activation barrier and react to form products. However, according to quantum mechanics, there is a possibility that particles are able to tunnel through barriers of finite energy. Hence, this means that reactions can occur even if the reactants collide with insufficient energy to overcome the activation barrier. For reactions which have a low activation barrier, the possibility for such tunneling increases, resulting in a rate of reaction larger than what would be predicted using the Transition state theory.
Exercise 2:
1. Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 is more destabilised as compared to H + HF (Relate this to the Potential Energy Surface that you observe) Je714 (talk) 14:49, 31 May 2017 (BST) . Hence the formation of H + HF from F + H2 is exothermic. The bond strength of HF is 568 kJ/mol which is larger than that of H-H which is 436 kJ/mol. Hence the energy released from the formation of the H-F bond is more than the energy required to break the bond, H-H.
2. Locate the approximate position of the transition state.
The approximate position of the transition state is when the distance between the H atoms is 0.74Å and the distance between F and H is 1.82Å.
Evidence of this is required (screenshots, explain your reasoning, etc.). Je714 (talk) 14:49, 31 May 2017 (BST)
3. Report the activation energy for both reactions.
The activation energy of F + H2 is 0.1880 kcal/mol and the activation energy of H + HF is 29.9013 kcal/mol.
Same here. We're not that interested in the number per-se, I want to see how and why you've reached these numbers. How did you calculate them is important to show understanding of the subject. Je714 (talk) 14:49, 31 May 2017 (BST)
4. In light of reactive trajectory for the F + H2 and the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
 |
The forward reaction is exothermic and hence, the reactants F + H2 are more destabilised and have a larger potential energy than the products, H +HF. Due to the conservation of energy, the total energy remains constant throughout the reaction. The decrease in potential energy when the products are formed is converted into kinetic energy in the form of translational and vibrational energy. The increase in vibrational energy can be seen from the strong oscillations of the product, HF, as the bond distances of HF fluctuates rapidly. As the number of vibrations per unit distance decreases in the products as compared to the reactants, it can also be seen that there is an increase in the translational energy of the products and H moves rapidly away from HF. However, it must be noted that the F is much larger than H, and hence would move slower. Furthermore, the hydrogen molecule also has a smaller bond distance and hence would be expected to vibrate a smaller distance. Thus, in the case of the reactants, it is possible for the hydrogen molecule to vibrate a larger number of times as the F approaches it and the increase in translational energy is not as easily seen.
This can confirmed experimentally using 2 methods:
|
5. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
 |
 |
 |
 |
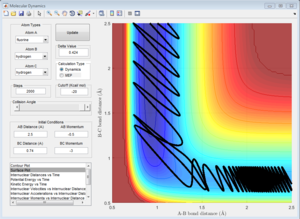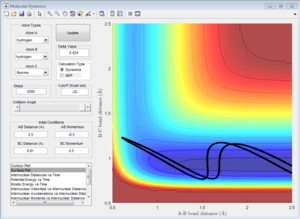
From the 4 examples in the above table, it can be seen that the total translational and vibrational energy of the reactants is not sufficient to determine whether a reaction occurs or not. Even though the last run has less total energy as the second run, the reactive trajectory is reactive. This can be explained using Polanyi's empirical rules. The formation of H + HF from F + H2 is exothermic, hence according to Hammond's Postulate, the structure of the activated complex is similar to that of the reactants and there is an early transition state. Using Polanyi's empirical rules, when there is an early transition state, the relative translational energy of the reactants is more effective in overcoming the activation barrier. This can be seen in the first run, where a large vibrational energy is needed for the reaction to occur. However, only a small increase in translational energy is required for the reaction trajectory to overcome the activation barrier and complete the reaction, as seen in the last example. Hence, the reaction is more efficient by using slightly more translational energy and much less translational energy is used.
 |
 |
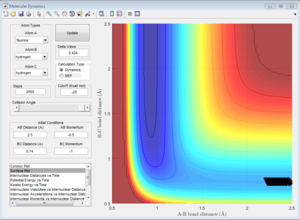
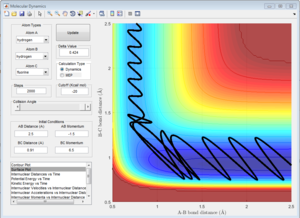The formation of F + H2 from H + HF is endothermic, hence according to Hammond's Postulate, the structure of the activated complex is similar to that of the products and there is a late transition state. Using Polanyi's empirical rules, for such reactions, the relative vibrational energy has a larger effect than the relative translational energy in determining if the reactants are able to overcome the activation barrier. This can be seen from the 2 examples in the table. Even though both examples have similar total energies, only the reaction which has a larger vibrational component of energy is able to overcome the activation barrier and the reaction completes. Hence, the reaction is more efficient when there is a larger vibrational component as compared to translational energy.
Good discussion using examples. Je714 (talk) 14:49, 31 May 2017 (BST)