MRD:zg916

Exercise one

Q1: What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

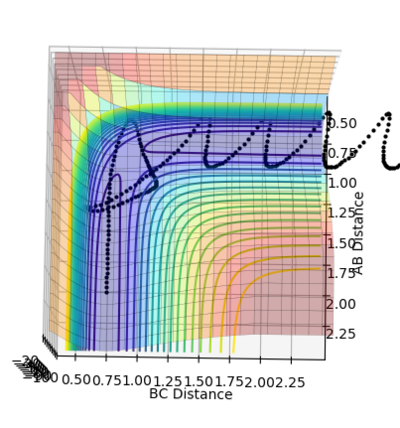
A: The gradient of the potential energy surface has two components: the partial derivative with respect to r₁ and r₂ respectively: V_r1 = $\frac{\partial V(r_1,r_2)}{\partial r_1}$ and V_r2 = $\frac{\partial V(r_1,r_2)}{\partial r_2}$. At minimum, both V_r1 and V_r2 are equal to zero. Transition state is defined as the maximum on the minimum energy path, which means it's a minimum point on potential energy curve. So, both V_r1 and V_r2 are equal to zero as well at a transition structure.

To distinguish between minima and transition structures, curvature should be used. Curvature is the second partial derivative with respect to r₁ and r₂. For minima and transition structures, V_r1r2 > 0. When V_r1r1•V_r2r2 - V²_r1r2 > 0, it's a minimum; when V_r1r1•V_r2r2 - V²_r1r2 < 0, it's a saddle point, i.e, a transition structure.

Q2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

A:

Figure 1. Internuclear Distance vs. Time

Figure 2. zoomed in at T.S.

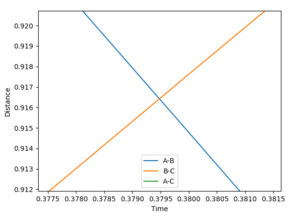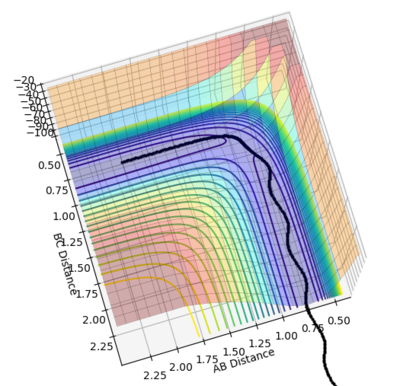
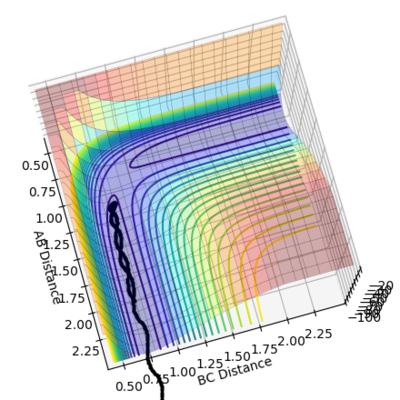
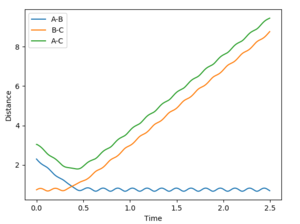
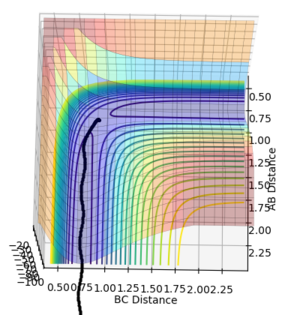
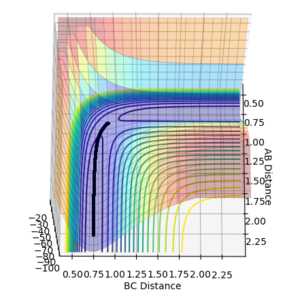
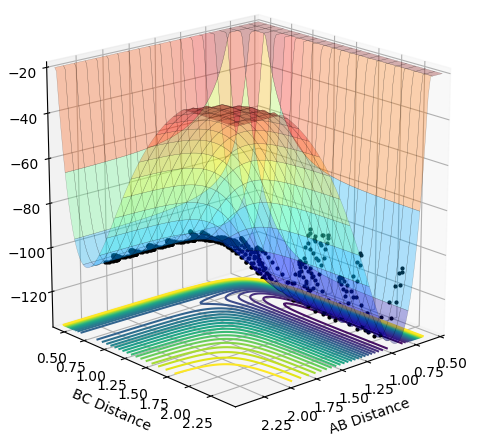
•Figure1 and figure1 shows the change in distance between H_A, H_B and H_C. The intercept as shown in figure 2 should indicate the position of transition state. When the initial momenta is set to be and the structure remains on transition state , H_A, H_B and H_C should remain stationary,i.e, the distance should be constant. This means that there should be no vibrations of the distance between H_A, H_B and H_C. By testing different initial distance,the position of transition state can be obtained when there are two straight line as shown in figure 3.

Figure 3. Internuclear Distance vs. Time when the initial distance is 0.90774 Å

•Position of transition state : 0.90774 Å

Q3: Comment on how the mep and the trajectory you just calculated differ.

A:

Figure 4. Dynamic surface plot(552 steps)

Figure 5. MEP surface plot(10000 steps)

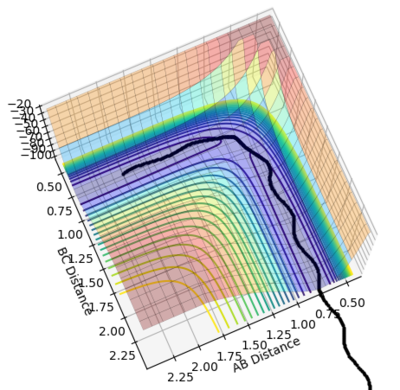
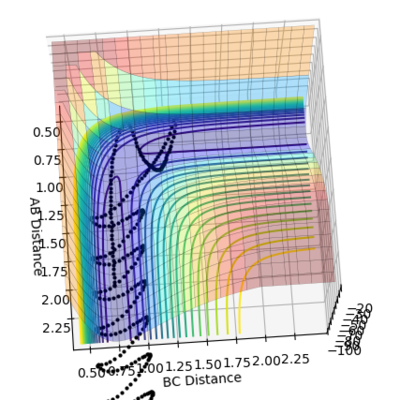
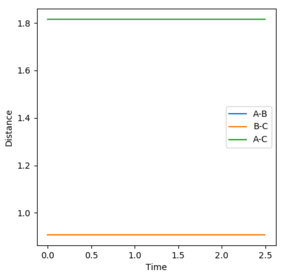
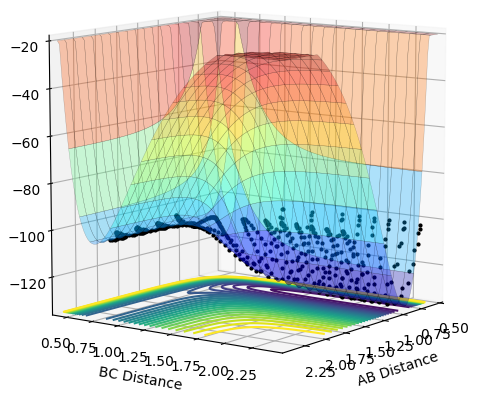
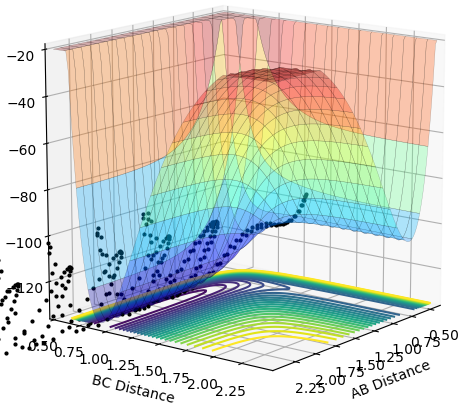
•As shown in figure 4 and 5, MEP gives a smooth trajectory without observable oscillations because it follows only the lowest energy path, ignoring the oscillations as the momenta is reset to zero for each step. In dynamic method, the trajectory follows the actual reaction pathway, showing the vibrations between atoms. To obtain a full trajectory, MEP needs a lot more steps than Dynamic(10000 vs 552). Because MEP measures the motion in infinitesimal fractions, and the velocity, thus the momentum is set to zero at each fraction.

Q3:Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

A:

Effect of momenta on reactivity

Set	p1	p2	Total energy	Type of trajectory	contour plot	Description
1	-1.25	-2.5	-99.119	Reactive	Figure 6. SET 1	The trajectory starts from reactants, passing through the transition state and reach product. This shows the initial energy is enough to overcome the energy barrier.
2	-1.5	-2.0	-100.456	Unreactive	Figure 7. SET 2	The trajectory starts from reactants, after reaching the transition state, it falls back to the reactants side. This indicates the initial energy is not enough.
3	-1.5	-2.5	-98.956	Reactive	Figure 8. SET 3	The trajectory starts from reactants, passing through the transition state and reach product. This shows the initial energy is enough to overcome the energy barrier.
4	-2.5	-5.0	-84.956	Unreactive	Figure 9. SET 4	The trajectory starts from reactants, after reaching the transition state, it falls back to the reactants side with an oscillating path. This indicates the initial energy is not enough.
5	-2.5	-5.2	-83.416	Reactive	Figure 10. SET 5	The trajectory starts from reactants and reaches the transition state. After falling back towards the reactants side, it recross the energy barrier and reach product with an oscillating path eventually. This shows the initial energy is enough to overcome the energy barrier.

Q5:State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

A:

Main Assumptions

•Chemical equilibrium between reactants and activated transition state complex

•Atoms have Boltzmann distributed energy in reactant state

•When applying TST, quantum-tunneling effects are assumed negligible and Born-Oppenheimer approximation is invoked

•Once the system attains the transition state, with a velocity towards the product configuration, it will not reenter the initial state region again

As shown in set4 and set5, it is possible for the system to fall back towards the reactant side and recross the energy barrier. This situation is ignored in TST, which means the predicted rate of reaction using TST should be higher than experiment. Also, it is possible for quantum tunneling to occur during reaction. Particles that tunnel through the potential barrier should have a lower energy because it undergoes exponential decay inside the barrier. This means that the actual energy may be lower than the predicted one.

Ng611 (talk) 23:20, 7 June 2018 (BST) A pretty good first section, although your discussion here is a little confused. I'm not sure what you're getting at with your penultimate sentence...

Exercise two

Q6: Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

A:F+H₂:

Figure 11. PES of F approaching H₂

This is an exothermic reaction. The energy of reactants is higher than that of products as shown in Fig11.

The bond strength of H-F is higher than H-H. This is in consistent with the experiment results, because the energy need to break the H-H bond is less that the energy released forming H-F bond.

H+HF:

Figure 12. PES of H approaching HF

This is an endothermic reaction.The energy of reactants is lower than that of products as shown in Fig12.(this particular graph shows an unreactive scenario due to insufficient initial conditions)

The bond strength of H-F is higher than H-H. This is in consistent with the experiment results, because the energy need to break the H-F bond is larger that the energy released forming H-H bond.

Q7:Locate the approximate position of the transition state.

A:F+H₂:

According to Hammond postulate, the transition state resembles the reactant in an exothermic reaction. This means that in the transition state, H-H should be much smaller than H-F. As shown in Fig11, the transition state should have a H-H bond length around 0.75 Å. By testing different value of H-H and H-F, the approximate position of the transition state can be obtained when the intermolecular distance is closest to constant given 0 initial momenta.

The approximate position should be d_HH=0.751 Å, d_HF=1.808 Å

H+HF:

According to Hammond postulate, the transition state resembles the product in an endothermic reaction. This means that in the transition state, H-H should be larger than H-F.As shown in Fig12, the transition state should have a H-F bond length around 1.810 Å.By testing different value of H-H and H-F, the approximate position of the transition state can be obtained when the intermolecular distance is closest to constant given 0 initial momenta.

The approximate position should be d_HH=0.746 Å, d_HF=1.810 Å

Q8: Report the activation energy for both reactions.

A: When the system has 0 initial momenta starts from a structure slightly deviated from the transition state towards the reactants, the system can automatically fall back to reactant side along the potential well.

F+H₂:

The initial conditions were set to be d_HH=0.761 Å, d_HF=1.818 Å with 0 initial momenta. The activation energy can be obtained from the energy vs time graph as shown in fig13.

Figure 13. Energy vs Time

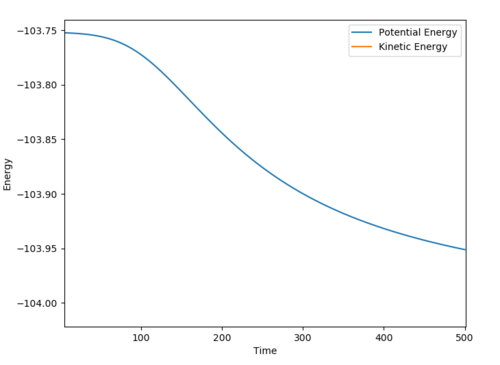
The activation energy = 0.105 kJ/mol

Ng611 (talk) 23:21, 7 June 2018 (BST) This is a little too low. It seems that you've not run your simulation for long enough!

H+HF:

The initial conditions were set to be d_HH=0.736 Å, d_HF=1.80 Å with 0 initial momenta. The activation energy can be obtained from the energy vs time graph as shown in fig14.

Figure 14. Energy vs Time

The activation energy = 30.116 kJ/mol

Q9: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

A:

Initial Conditions

FH distance	2.3
HH distance	0.74
FH momentum	-2.0
HH momentum	0

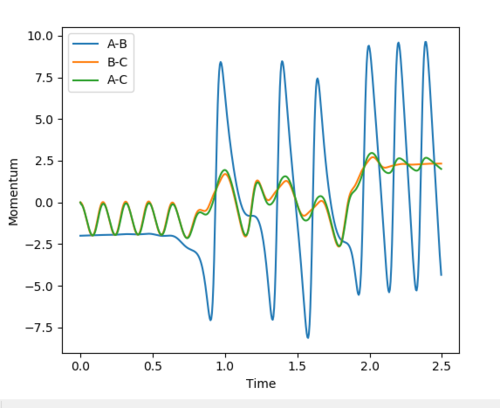
As shown in fig 15, the trajectory shows the reaction reaches product side so it is reactive.

Figure 15. reaction trajectory for F+H₂

As shown in fig16 below, the increase in the momenta proves that the vibrational energy of the product is much larger than reactants. In this exothermic reaction, the translational energy of H-H is converted to the vibrational energy of H-F.

The energy transfer can be confirmed by using IR spectroscopy, as the signal reflects the vibrational bond energy in molecules. To monitor the reaction process, flow method can used to show the different components in the reaction mixture: pure H₂ at first, mixture of H₂ and HF in the middle of the reaction, and pure HF at last.

Ng611 (talk) 23:24, 7 June 2018 (BST) IR spectroscopy is a good choice -- what would you expect to see? Not sure how the flow method fits in though.

Figure 16. internuclear momenta vs time for F+H₂

Q10: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state. In an exothermic reaction, the transition state resembles the reactants, i.e. early transition state. The initial momenta of the reactants must be large enough to provide sufficient translational energy to overcome the energy barrier.

A: In most chemical reactions, an energy barrier must be overcome in order for the reaction to occur.Usually, vibrational energy is more efficient in promoting a late-barrier reaction (i.e. a transition state resembles the products and is endothermic) than translational energy, and vice versa for an early barrier reaction which is exothermic.

In an exothermic reaction, the transition state resembles the reactants, i.e. early transition state. The initial momenta of the reactants must be large enough to provide sufficient translational energy to overcome the energy barrier. Otherwise, the reaction trajectory may fall back to reactants region and the reaction is unsuccessful.

In an endothermic reaction,the transition state resembles the products, i.e. late transition state. Enough vibrational energy is needed to overcome the energy barrier.

Ng611 (talk) 23:24, 7 June 2018 (BST) Good explanation, although you needed to back this up with example simulations.

Reference

Ng611 (talk) 23:25, 7 June 2018 (BST) Some really good bits in this report, although you let yourself down by not including examples in the second section -- this was a significant part of the report.