MRD:ytl115report

(Fv611 (talk) 11:49, 25 May 2017 (BST) Very good wiki overall - good job!)

Exercise 1: H + H₂ system

Minimum and Transition States

Gas phase collision and reaction between an atom and diatomic molecule in a linear configuration

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

At both the minimum and transition structures, the total gradient of the potential energy surface will be zero. In order to distinguish between a minima and transition structure, the second derivative of the potential energy surface against displacement can be found. A positive value will indicate a minimum while a negative value indicates a maximum, or transition structure.

Dynamics from the Transition State region

Locating the transition state

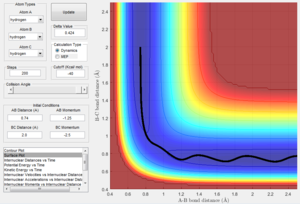
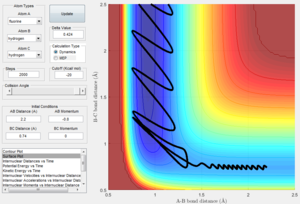
Report your best estimate of the transition state position (r_ts) and explain your reasoning.

r_ts = 0.908 Å

Looking at figure 1, it can be seen that the vibrations of the atoms are at a minimum at this distance from each other, suggesting that this is an equilibrium position since the gradient of the potential energy surface would be zero.

Also, with minimal vibration, the kinetic energy of the molecules would be at a minimum and hence the potential energy of the molecules would be at a maximum. This would indicate a transition state as in a transition state, the gradient (first derivative) of the PES is zero but its second derivative would be a negative value (concave downward).

Trajectories

Table 1. PES plots of reaction trajectories from transition state
MEP PES plot of reaction trajectory from transition state	Dynamic PES plot of reaction trajectory from the transition state

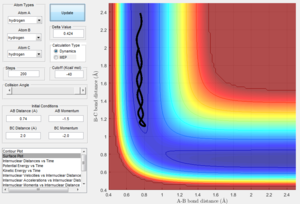
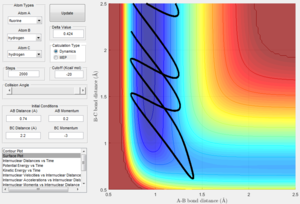
Comment on how the mep reaction path and the dynamic trajectory differ.

In the minimum energy path shown in Table 1, the velocity is reset to zero after every time step. As such, the trajectory will only follow a path where the energy is at a minimum i.e. the bottom of the potential energy surface. The direction of movement of the particles is thus disregarded as the velocity is not considered.

In a dynamic calculation, however, the velocity of the particles is not ignored. Also, because the particles possess an initial velocity, the trajectory will show an oscillation from the minimum position.

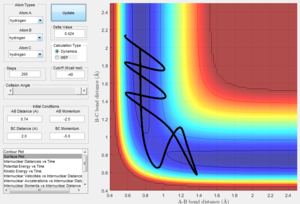
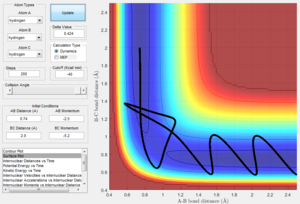
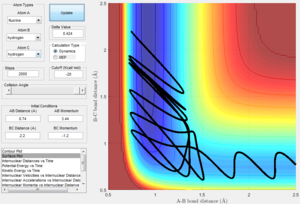
Reactive and Unreactive Trajectories

Changing the initial distances between atoms (r₁, r₂) and their momenta (p₁, p₂) will result in a change in the reaction trajectory. Table 2 below shows 5 different trajectories calculated for a system with r₁ = 0.74 and r₂ = 2.0.

Table 2. Reaction trajectories for different input momenta
#	p₁	p₂	Reactivity	Notes
1	-1.25	-2.5	Reactive	H_c approaches H_a-H_b. There is sufficient energy to pass through the transition state and the reactants react to form H_b-H_cand H_a. H_a moves further away from H_b-H_cand the H_b-H_c bond oscillates due to vibrational energy.
2	-1.5	-2.0	Unreactive	H_c approaches H_a-H_b. There is insufficient energy to pass through the transition state and the reactants rebound from the barrier. H_c moves further away from H_a-H_b.
3	-1.5	-2.5	Reactive	H_c approaches H_a-H_b. There is sufficient energy to pass through the transition state and the reactants react to form H_b-H_cand H_a. H_a moves further away from H_b-H_cand the H_b-H_c bond oscillates due to vibrational energy. However, along the approach coordinate, H_a-H_boscillates with vibrational energy as well. This is possibly due to a larger input momentum cf. case 1, where there was a lower input momentum for H_a-H_band the reactant did not oscillate.
4	-2.5	-5.0	Unreactive	H_c approaches H_a-H_b. There is sufficient energy to pass through the transition state and the reactants react to form H_b-H_cand H_a. However, the products pass through the transition state again to re-form the reactants, in a phenomenon known as barrier recrossing. This is possibly due to an excess amount of input momentum, and the re-formed reactants are clearly seen to vibrate with a large amount of vibrational energy.
5	-2.5	-5.2	Reactive	H_c approaches H_a-H_b. There is sufficient energy to pass through the transition state and the reactants react to form H_b-H_cand H_a. However, the products pass through the transition state again to re-form the reactants, and then once more to form the products, crossing the transition state a total of three times. This is possibly due to there being sufficient vibrational energy, as the input energy for the H_b-H_c is greater than that of case 4. The products thus re-form with a large amount of vibrational energy, which is reflected in the large amplitudes of their oscillation.

Transition State Theory

State what the main assumptions of Transition State Theory are.

Transition State theory is used to qualitatively understand how chemical reactions take place. The basis of this theory is that it is possible to define a surface in coordinate space and to calculate the flux of trajectories that pass through this surface from the reactants to the products without turning back, of which the flux is known as the reactive flux.^[1] However, there are several assumptions made in this theory, which are outlined below. It is assumed that:

A special type of chemical equilibrium (quasi-equilibrium) exists between reactants and activated transition state complexes

This assumes that even when the reactants and products are not in equilibrium with each other, the activated complexes are in quasi-equilibrium with the reactants. By doing so, this allows for a rate constant to be calculated as the rate is then directly proportional to the concentration of these complexes multiplied by the frequency with which they are converted into products.

Molecules are distributed amongst their states according to the Boltzmann distribution
Atomic nuclei behave according to classical mechanics

This means that sufficient energy must be provided in order to cross the transition state and tunnelling does not occur

The reaction system will pass over the lowest energy saddle point on the potential energy surface

While this assumption holds true and works for reactions at low temperatures, it starts to break down at higher temperatures, where higher vibrational states are accessible and become populated. The motion of particles becomes more complex and collisions may lead to transition states far away from the lowest energy saddle point.

How will Transition State Theory predictions for reaction rate values compare with experimental values?

The transition state theory predicts higher reaction rate values compared with experimental values as a result of its assumptions. As it does not take into account the phenomena of barrier recrossing, it will assume that the reaction will proceed once the barrier is crossed once. However, this is not always the case, as seen from examples above, where the reaction may only proceed after the barrier is crossed several times.

Also, the theory assumes that the reaction system will pass through the lowest energy saddle point on the PES in a reactive trajectory. This means that the input energy for a reaction to occur would be equal to the activation energy. This is not always true, especially at higher temperatures where higher energy saddle points are accessed instead, resulting in a larger energy required for the reaction to proceed. It is also not considered in this theory the distribution of energy - more energy than simply the activation energy might be required if it is not distributed to the appropriate form (translational, vibrational etc). Since the rate constant is proportional to the negative exponential of energy, this would result in a lower rate constant for the reaction compared to what is predicted by TS theory.

Furthermore, in the transition state theory, only three states are considered - the reactant, activated complex and product. In reality, there may be more states than these and the entire potential energy surface of the reaction system must be taken into account.

(Fv611 (talk) 11:49, 25 May 2017 (BST) Very good answer.)

Exercise 2: F-H-H system

PES inspection

Reaction Energetics

Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

As seen in Figure 4, the energy is lower along the A-B axis, which means that the H-F system has lower energy compared to H-H. A reaction between a fluorine atom and hydrogen gas would be exothermic and a reaction between hydrogen fluoride and a hydrogen atom would thus be endothermic. This is in line with the bond energies of the compounds, as the bond dissociation energy of H-H is 436 kJ mol^-1 while for H-F it is 570 kJ mol^-1.^[2]

Table 3. Energetics of F-H-H system
Reaction	Energetics
F + H₂ --> HF + H	Exothermic
H + HF --> H₂ + F	Endothermic

Transition State

Locate the approximate position of the transition state.

Transition state is located at r_HF = 1.81 Å and r_HH = 0.745 Å

The position of the transition state can first be approximated by considering Hammond's Postulate, which states that the transition state will resemble either the reactants of the products, depending on which it is closer in energy to. In this case, the transition state would lie closer to the F + H₂ side, and is thus found by first setting the B-C distance to be similar to the actual H-H bond length of 74 pm and adjusting the positions of the atoms from there. In figure 5, which shows the plot of internuclear distances against time at the transition state, the oscillation of the atoms at the point is close to zero, which indicates a saddle point and thus the transition state.

Activation energy

Report the activation energy for both reactions.

Table 4. Activation energies for F-H-H system
Reactants	TS --> F + H₂	TS --> H + HF
Plot of potential energy against time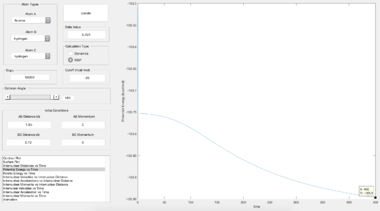
Energy of products / kcal mol^-1	-103.9	-133.9
Energy of TS / kcal mol^-1	-103.3
Activation energy / kcal mol^-1	0.6	30.6
Lit. activation energy / kcal mol^-1^[3]	1.6	31.9

Reaction Dynamics

Release of reaction energy

Identify a set of initial conditions that results in a reactive trajectory for the F + H₂. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

Table 5. Reaction dynamics for F + H₂ --> HF + H
	PES reactive trajectory	Internuclear Momenta against Time
F + H₂ --> HF + H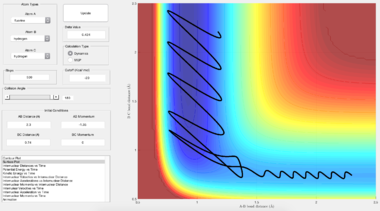

Looking at the plot of internuclear momenta against time for a reactive trajectory, it can be seen that the products have much greater vibrational energy compared to the reactants. This shows that one form of the energy that comes from the release of reaction energy is vibrational energy (periodic oscillation between potential and kinetic energy) in the products. This form of energy lies in the infra-red spectrum of light and can hence be detected through spectroscopic techniques such as IR chemiluminescence.^[4] This technique was first reported by J. C. Polanyi (who also proposed the Polanyi rules for reaction dynamics below) and involves the measurement of infrared emission of the a reaction in order to determine its chemical rate constant.

Another form of release of reaction energy could also be in the form of heat, which can be measured by isolating the reaction system and monitoring the temperature of the reaction.

Influence of distribution of energy on reactivity

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Table 6. Illustration of Polanyi's rules
	Translation	Vibration	Notes on Reactivity
Early Barrier			Early barrier: Barrier lies along approach (reagent) coordinate Translational motion along approach coordinate gives rise to reactive trajectory.
Late Barrier			Late barrier: Barrier lies along the coordinate of separation (products) Vibrational motion along approach coordinate gives rise to reactive trajectory.

As seen from Table 6 above showing four different examples, for a reaction to occur, it must not only possess sufficient energy, but the correct distribution of the various forms of energy as well. For example, the energy distribution between translation and vibration will influence the efficiency of the reaction. In order for the reactant molecules to overcome the energy barrier, they need to approach the point with the correct orientation, leading to a successful reaction. Looking at the examples above, for an exothermic reaction such as F + H₂ --> HF + H which has a early barrier, translational motion is required in order to pass the saddle point where the transition state is located. For the reverse reaction, however, which is endothermic, because the transition state is located closer towards the product (a late barrier), vibrational motion would be more effective towards surmounting the barrier due to the motion along the axis of the products.

Stated still more simply, a barrier along the approach coordinate is most efficiently surmounted by motion along the approach coordinate (reagent translation), whereas a barrier along the coordinate of separation is most efficiently surmounted by motion along that coordinate (reagent vibration).^[5] A early or late barrier can simply be determined by considering the energetics of the reaction - according to Hammond's postulate, if a reaction is exothermic, the transition state will resemble the reactants and hence the barrier will be an early or reactant-like one. Conversely, for an endothermic reaction, the transition state will resemble the products more closely and the barrier is more likely to be a late, or product-like one.

(Fv611 (talk) Great discussion. Well done!)

References

↑ R. Silbey, R. Alberty, M. Bawendi, Physical Chemistry, John Wiley & Sons, 4th edn, 2005, pp. 687.
↑ Luo, Y. R., Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, FL, 2007
↑ J. C. Polanyi, J. L. Schreiber, Faraday Discuss. Chem. Soc., 1977, 62, 267-290
↑ L.T. Cowley, D.S. Horne, J.C. Polanyi, Chem. Phys. Lett., 2013, 589, 3-6
↑ J. C. Polanyi, Acc. Chem. Res, 1972, 5, pp 161–168

[1] R. Silbey, R. Alberty, M. Bawendi, Physical Chemistry, John Wiley & Sons, 4th edn, 2005, pp. 687.

[2] Luo, Y. R., Comprehensive Handbook of Chemical Bond Energies, CRC Press, Boca Raton, FL, 2007

[3] J. C. Polanyi, J. L. Schreiber, Faraday Discuss. Chem. Soc., 1977, 62, 267-290

[4] L.T. Cowley, D.S. Horne, J.C. Polanyi, Chem. Phys. Lett., 2013, 589, 3-6

[5] J. C. Polanyi, Acc. Chem. Res, 1972, 5, pp 161–168

[1]

[2]

[3]

[4]

[5]

Exercise 1: H + H2 system