MRD:yrt13
EXERCISE 1: H + H2 system
Value of gradient at minimum and at transition state.
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The total gradient of the potential energy surface at a minimum is zero. The total gradient of the potential energy surface at a transition structure is also zero.
However, they can be distinguished when the curvature of the potential energy surface is observed[1]. At the minima, the curvature has a positive second derivative (U-shaped or concave). This means that the gradient of the potential energy surface changes from negative to zero, and then from zero to positive after. In the potential energy surface, this is the lowest point in the region where a 'hole' is observed.
At the transition state, the curvature is a saddle point[1] and its second derivative also has a value of zero. This means that the gradient of the potential energy surface changes from negative (or positive) to zero, and then from zero to negative again (or positive again). The sign of the gradient remains the same before and after the saddle point. The transition state saddle point is also known as the maximum of the minimum energy path and it links the reactants and products.
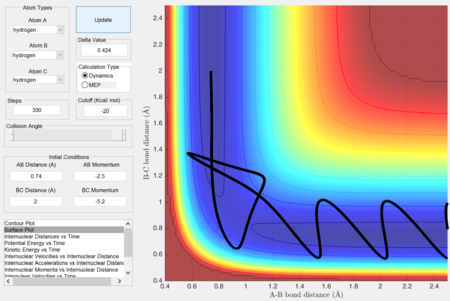
Estimate of transition state position (rts).
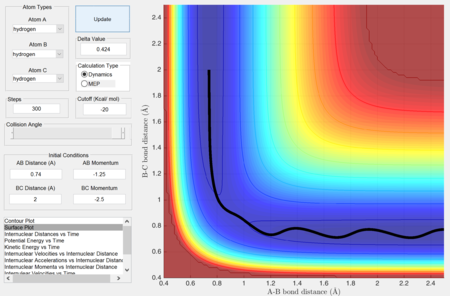
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
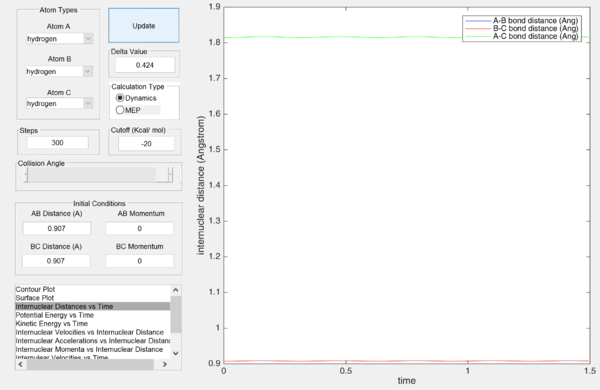
rts = 0.907 Å (Angstrom)
As seen from the "Internuclear Distances vs Time" graph, the oscillations (of the atoms) are minimal, suggesting that they are near their equilibrium position. Furthermore, this also shows that this state has minimum (potential) energy and hence corresponds to the minimum of the potential energy surface, which is the transition state.
Moving away from this state will result in oscillations.
Dynamics vs mep.
Comment on how the mep and the trajectory you just calculated differ.
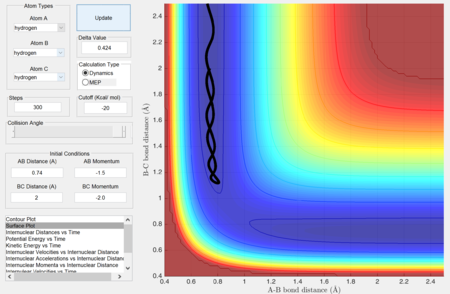
In mep, the trajectory produced is a straight line and it follows the the valley floor to the final product without oscillation.
This is because in mep, the velocity resets to zero after each step. Hence, the trajectory will only follow and move in the direction of steepest descent in each time step. Therefore, the trajectory corresponds to the minima of the potential surface (valley floor).
However, when the calculation type is changed back to dynamics, an oscillatory trajectory is observed and the trajectory becomes a wave. This is because the atom has an initial velocity, which influences its motion and path.
Reactive or unreactive trajectory?
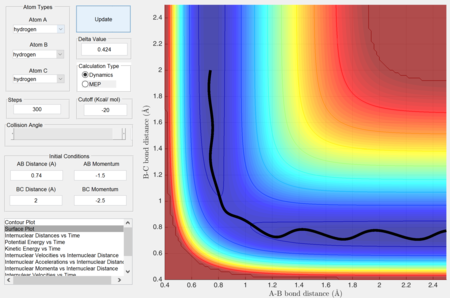
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | Reactive/Unreactive | Screenshot of Trajectory | Description |
|---|---|---|---|---|
| -1.25 | -2.5 | Reactive |  |
C approaches A-B. There is sufficient energy to pass through the transition state and the reactants react to form B-C + A. A moves further away from B-C.
The B-C bond oscillates due to vibrational energy. |
| -1.5 | -2.0 | Unreactive |  |
C approaches A-B but does not react as there is insufficient energy (and possibly inappropriate levels of vibrational motion) to cross the transition state. Thus, the trajectory bounced off the barrier. C rebounds and moves further away from A-B. |
| -1.5 | -2.5 | Reactive |  |
C approaches A-B. There is sufficient energy to pass through the transition state and the reactants react to form B-C + A. A moves further away from B-C.
The B-C bond oscillates due to vibrational energy. The initial trajectory also seem to oscillate, unlike in the first case. This could be due to the larger initial momentum of A-B, leading to higher kinetic and vibrational energy. However, the products still have more vibrational excitation than the reactants. |
| -2.5 | -5.0 | Unreactive |  |
C approaches A-B but does not react. In this case, the system has sufficient energy and crosses the transition state, however, the system then reverts back to the reactants as seen from the trajectory. This is known as Barrier Recrossing.
The reactants are reformed with large amounts of vibrational excitation. |
| -2.5 | -5.2 | Reactive |  |
C approaches A-B. There is sufficient energy to pass through the transition barrier thrice (including one barrier recrossing) and hence, the reactants react to form B-C + A. A then moves further away from B-C.
The products have large amounts of vibrational excitation. |
Main assumptions of Transition State Theory.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The transition state theory is used to qualitatively understand how chemical reactions take place. There are a few assumptions[2][3] made in this theory.
1. The quasi equilibrium assumption is made. Basically, this theory assumes that a special chemical equilibrium (known as the quasi equilibrium) exists between the activated transition state complex and the reactants. Even when the products and reactants are not in equilibrium with each other, the reactants are in quasi-equilibrium with the activated transition state complex.
2. This theory assumes that the lifetime of each intermediate is long enough to reach a Boltzmann distribution of energies before moving on to the next step.
3. This theory assumes that atomic nuclei behave according to classic mechanics. This also means that this theory assumes that sufficient energy must be provided for the system to cross the activation barrier and to react. Tunneling does not occur.
4. This theory assumes that the reaction system will cross/pass through the (lowest energy) saddle point on the potential energy surface.
5. This theory only considers 3 states/geometries - the reactants, the activated complex (at the saddle point) and the products. All other states and geometries are not considered.
6. This theory assumes that barrier recrossing is not possible.
The Transition State Theory predictions for reaction rate values are different from experimental values. This is because the various assumptions made above do not hold true in a real situation. For example, the quasi-equilibrium does not always hold true and the lifetime of intermediates/activated transition state complexes are not long enough, since they are about 10−13 seconds (almost zero!). Also, atomic nuclei can behave according to quantum mechanics and it is possible for tunneling and barrier recrossing to occur. Also, in reality, the entire potential energy surface is considered and there are other possible states/geometries other than the reactant, product and activated complex state.
Overall, the Transition State Theory predictions for reaction rate values may be higher than experimental values. This is because it does not account for barrier recrossing and it assumes that the amount of energy required for the reaction to occur is the activation energy. However, it does not consider the energy distribution (across various vibrational modes, for example) and thus predict a higher value. This can be corrected by considering the translational and vibrational partition functions. Furthermore, the probability of the system passing through the saddle point, a small point on the entire potential energy surface, is very small and hence this assumption causes inaccurate predictions.
EXERCISE 2: F - H - H system
Reaction Energetics
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
F + H2 -> HF + H is an exothermic reaction, as seen from the potential energy surface.
H + HF -> H2 + F is an endothermic reaction, as seen from the potential energy surface.
| No. | Reaction | Energetics |
|---|---|---|
| 1 | F + H2 -> HF + H | Exothermic |
| 2 | H + HF -> H2 + F | Endothermic |
The bond energy of H-F is larger than the bond energy of H-H. The H-F bond strength is stronger than the H-H bond strength. This is supported by literature value[4] where BE(H-H) = 432 kJ mol-1 and BE(H-F) = 565 kJ mol-1
Approximate Position of Transition State.
Locate the approximate position of the transition state.
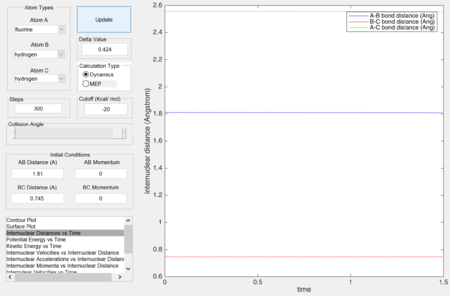
The approximate position of the transition state is where
rHF = 1.81 Å and
rHH = 0.745 Å
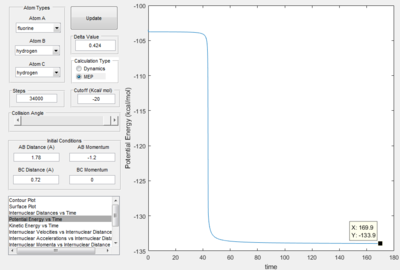
Activation Energy of reactions.
Report the activation energy for both reactions.
 |
 |
| Transition state -> H-F + H | Transition state -> H-H + F |
Energy of transition state = -103.3 kcal mol-1
Energy of H-F and H = -133.9 kcal mol-1
Energy of H-H and F = -103.9 kcal mol-1
Therefore, Activation energy of the F + H2 -> HF + H reaction is 0.6 kcal mol-1
Activation energy of H + HF -> H2 + F reaction is 30.6 kcal mol-1
| Energy of transition state / kcal mol-1 | Energy of H-F + H / kcal mol-1 | Energy of H-H + F / kcal mol-1 |
|---|---|---|
| -103.3 | -133.9 | -103.9 |
| No. | Reaction | Activation Energy / kcal mol-1 | Literature Value[5] / kcal mol-1 |
|---|---|---|---|
| 1 | F + H2 -> HF + H | 0.6 | -1.6 |
| 2 | H + HF -> H2 + F | 30.6 | -31.9 |
Release of reaction energy.
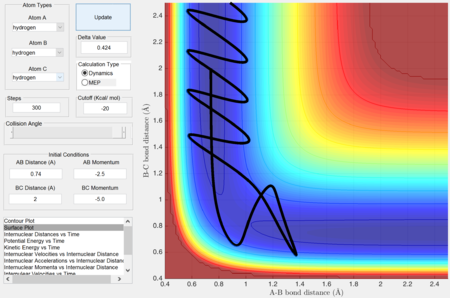
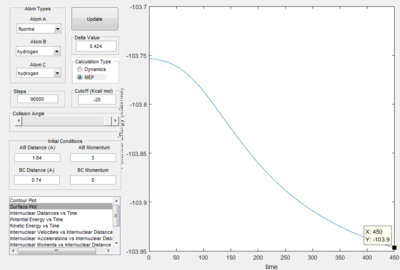
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
 |
 |
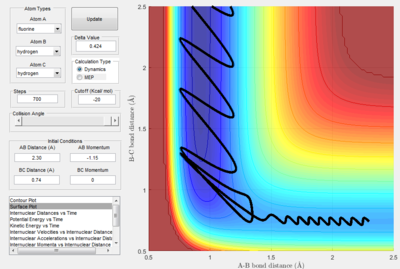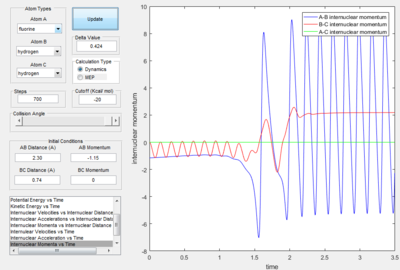As seen from the "Internuclear Momenta vs Time" plot, the H-F bond oscillates with great vibrational energy.
The reaction energy is released as vibrational energy (inter-converting between potential energy and kinetic energy). As the products possess vibrational energy, it is possible to use spectroscopic techniques that involve infra-red (IR) waves such as infra-red chemiluminescence[6] to measure the vibrational energy (and distribution) of the product.
The reaction energy could also be lost and released as heat. This can be confirmed by monitoring the temperature of the reaction in a closed system.
Distribution of energy vs Efficiency of reaction.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
For a reaction to occur, the reactants must not only possess sufficient energy, but the energy must also be distributed in the right manner. For example, the energy distribution between various modes, such as translational and vibrational modes, will affect the efficiency of the reaction. This is because reactant molecules must approach at the right orientation with the right energy distribution in order to react successfully.
According to Polanyi's empirical rules[7], the most effective way to overcome a barrier along the coordinate of approach (an 'early' or 'reactant-like' barrier) is by motion along the reactant translational degree of freedom. On the other hand, the most effective way to overcome a barrier along the coordinate of separation (a 'late' or 'product-like' barrier) is by the motion along the reactant vibrational degree of freedom. In other words, if we want to overcome an 'early' or 'reactant-like' barrier, it is not very effective to increase the vibrational energy of the reactants.
Therefore, to maximize the efficiency of the reaction, one must consider the nature and properties of the barrier and provide sufficient translational and vibrational energy in an appropriate distribution. The transition state must also be considered. The position of the transition state influences and determines the position and height of the barriers. For example, in an exothermic reaction, the transition state resembles the reactants more according to Hammond's Postulate, and hence the barrier will be an 'early' or 'reactant-like' one. Also, in an endothermic reaction, the transition state resembles the products more according to Hammond's Postulate, and hence the barrier will be a 'late' or 'product-like' one. This is how the distribution of energy and efficiency of the reaction is influenced by the position of the transition states.
References
- ↑ 1.0 1.1 F. Bernardi, M. Olivucci and M. A. Robb, Chem. Soc. Rev., 1996, 25, 321–328.
- ↑ K. J. Laldler and M. C. King, J. Phys. Chem., 1983, 87, 2657–2664.
- ↑ H. Eyring, J. Chem. Phys., 2010, 107.
- ↑ Y. R. Luo, Comprehensive handbook of chemical bond energies. CRC press., 2007.
- ↑ Polanyi, J.C. and Schreiber, J.L., 1977. The reaction of F+ H 2→ HF+ H. A case study in reaction dynamics. Faraday Discussions of the Chemical Society, 62, pp.267-290.
- ↑ The Journal of Chemical Physics 64, 586 (1976); doi: 10.1063/1.432249
- ↑ B. Jiang and H. Guo, J. Chem. Phys., 2013, 138.