MRD:yht17
On a potential energy surface for a reaction, the transition point is a saddle point, a type of stationary point. Since in this case, the potential energy surface is well defined as a function of two parameters (E(r1,r2)), a stationary point can be found where Er1 = Er2 = 0. In this potential energy surface, the only stationary point should be the saddle point, but this can be confirmed by checking that Er1r1Er2r2 - Er1r2Er2r1 < 0.
How could one distinguish between Saddle point and a local minimum? Fdp18 (talk) 19:27, 28 May 2019 (BST)
H + H2
The transition state of this system should lie along the line r1 = r2.
By choosing points along this line and looking at the internuclear distances versus time graph, the transition point can be found to a high precision.
A precise estimate of the transition state is at r1 = r2 = 0.9077424979.
The words 'precise' and 'estimate' are usually not used together. Also, think about the precision to which you reported the value and whether it is sensible (in terms of heisenberg's uncertainty principle) Fdp18 (talk) 19:26, 28 May 2019 (BST)
Starting from a point near the transition state (r1 = 0.9077424980 ,r2 = 0.9077424979), a minimum energy path and reaction dynamics trajectory was calculated.
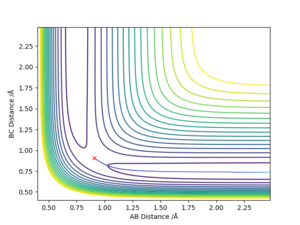
The MEP does not have any vibrations as it follows the bottom of the valley at all times. The dynamics trajectory results in the molecule ending up with vibrations.
If instead of r1 being changed from the transition state, r2 was increased a bit, the trajectories would follow the mirror image of the trajectories above.
Halfway through the dynamics trajectory above, we have the following values:
| AB distance | 2.27252926913964 |
| BC distance | 0.730339007221138 |
| AB momentum | 2.44110927644702 |
| BC momentum | 1.42865247530777 |
If a calculation were run starting with these values but with reversed momenta, we would expect the trajectory to go very close to the transition state, then return along the same trajectory.
We see that the trajectory does indeed go very close to the transition state, and in fact stays near there for a while, before returning along the same trajectory.
That is actually very nice, and it shows that you understand what you are doing here. Fdp18 (talk) 19:29, 28 May 2019 (BST)
A few calculations were performed with different starting momenta but with the same starting distances (r1 = 0.74, r2 = 2.0):
| p1 | p2 | Etot | Reactive? | Trajectory | Quick description |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.108 | Yes | 
|
Trajectory passes near transition state |
| -1.5 | -2.0 | -100.456 | No | 
|
Trajectory doesn't reach near transition state |
| -1.5 | -2.5 | -98.956 | Yes | 
|
Trajectory passes near transition state |
| -2.5 | -5.0 | -84.956 | No | 
|
Trajectory goes around transition state to the other side but goes back around the transition state to reform reactants |
| -2.5 | -5.2 | -83.416 | Yes | 
|
Trajectory goes past transition state three times |
This suggests that it is very difficult to predict whether a set of starting conditions results in a reaction.
A main assumption of transition state theory is that once the system passes the transition state into the products, it does not return to the reactants. From the above results, we see that when the transition state is passed, the system can pass over the transition state again to return to the products, and can in fact pass over the transition state multiple times before settling into reactants of products. This means that reaction rates obtained using transition state theory would be higher than experimental values.
At this point, it would be good to actually state the main assumptions and then put them into context, together with a proper reference to the theory. Fdp18 (talk) 19:31, 28 May 2019 (BST)
F - H - H system
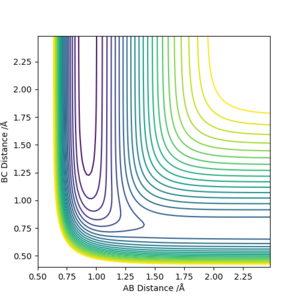
From this contour, we can see that F + H2 -> HF + H is exothermic and HF + H -> F + H2 is endothermic. This means that the H-F bond is stronger than the H-H bond.
A good estimate of the transition state is at rFH = 1.810753, rHH = 0.744879. This was done by choosing a point visually near near the saddle point on the potential surface and amending it based on the trajectory from that point.
The activation energy starting on both sides on the transition state can be find by calculating the MEP down both sides, then taking the difference between the starting and ending energies.
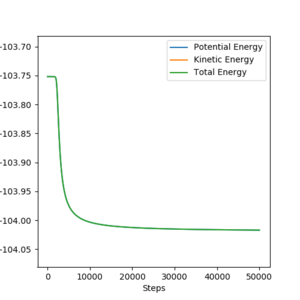
| Reactants | Starting energy | Ending energy | Activation energy |
|---|---|---|---|
| HF + H | -103.752 | -133.978 | 30.226 |
| F + H2 | -103.752 | -104.017 | 0.255 |
Reasonable estimate, especially since you've used sufficient time steps. Fdp18 (talk) 19:34, 28 May 2019 (BST)
Starting from F and H2, one set of starting conditions that results in a reaction is as follows:
| F-H distance | 2.4 |
| H-H distance | 0.7 |
| F-H momentum | -2 |
| H-H momentum | 1 |
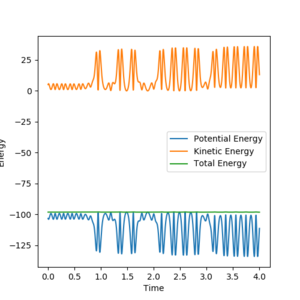
This calculation shows that over the course of the reaction, potential energy is converted to vibrational energy. This could be confirmed experimentally by reacting F2 with H2. Although energy would be used to break the F-F bonds, the reaction should still release energy. When this reaction happens, the vibrational energy manifests as heat energy.
Several calculations were performed with rFH = 2.4, rHH = 0.74, pFH = -0.5 and pHH between -3 and 3.
| pHH | Etot | Reactive? | Quick description |
|---|---|---|---|
| -3 | -96.279 | No | The central H atom moves to the F atom once then moves back and stays |
| -2.95 | -96.552 | No | The central H atom moves between the F atom and the H atom 10 times before staying with the H atom |
| -2.9 | -96.819 | No | The central H atom moves between the F atom and the H atom 4 times before staying with the H atom |
| -2.85 | -97.082 | No | The central H atom moves between the F atom and the H atom 6 times before staying with the H atom |
| -2.8 | -97.339 | Yes | The central H atom moves between the F atom and the H atom 3 times before staying with the F atom |
| -2.7 | -97.839 | No | The central H atom moves to the F atom once then moves back and stays |
| -2.6 | -98.319 | No | The central H atom moves to the F atom once then moves back and stays |
| -2.5 | -98.779 | No | The central H atom moves between the F atom and the H atom 4 times before staying with the H atom |
| -2.3 | -99.639 | No | The trajectory does not pass the transition state |
| -2 | -100.779 | No | The trajectory does not pass the transition state |
| -1 | -103.279 | No | The trajectory does not pass the transition state |
| 0 | -103.779 | No | The trajectory does not pass the transition state |
| 1 | -102.279 | No | The trajectory does not pass the transition state |
| 2 | -98.779 | No | The central H atom moves between the F atom and the H atom 4 times before staying with the H atom |
| 2.3 | -97.339 | Yes | The central H atom moves between the F atom and the H atom 7 times before staying with the F atom |
| 2.5 | -96.279 | No | The central H atom moves to the F atom once then moves back and stays |
| 2.6 | -95.719 | No | The central H atom moves to the F atom once then moves back and stays |
| 2.7 | -95.139 | No | The central H atom moves to the F atom once then moves back and stays |
| 2.8 | -94.539 | No | The central H atom moves between the F atom and the H atom 4 times before staying with the H atom |
| 2.85 | -94.232 | No | The central H atom moves between the F atom and the H atom 6 times before staying with the H atom |
| 2.9 | -93.919 | No | The central H atom moves to the F atom once then moves back and stays |
| 2.95 | -93.602 | No | The central H atom moves to the F atom once then moves back and stays |
| 3 | -93.279 | Yes | The central H atom moves between the F atom and the H atom 11 times before staying with the F atom |
We can see that having enough vibrational energy is not sufficient to result in a reaction. Even if the vibrational energy is in excess of the activation energy, the trajectory may not pass the transition state, and even if it does, it usually results in no reaction.
A calculation was performed with rFH = 2.4, rHH = 0.74, pFH = -0.8 and pHH = 0.1. The total energy is -103.484, just enough to go over the transition state. The energy is mostly kinetic, there is very little vibrational energy. This results in a reaction.
A calculation was performed with rFH = 0.92, rHH = 2.4, pFH = -14 and pHH = -15, representing the reaction with the reactants HF + H with very little HF vibrational energy but colliding into H at a high speed. The total energy is -15.754, far in excess of the transition state.
We can see that this results in no reaction, but it is possible to use similar conditions that result in a reaction: rFH = 0.92, rHH = 2.4, pFH = -19 and pHH = -20. The total energy is +76.088, which is enough for complete dissociation, but that does not occur in this case.
This is reactive, but it is possible for starting conditions with less total energy to react.
A setup was found by reducing the collision speed and increasing the vibrational energy that also results in a reaction: rFH = 0.92, rHH = 2.4, pFH = -14.3 and pHH = -7.15. The total energy is -77.408, above the transition state but much lower than with the above conditions.
Polanyi's rules say that for an exothermic reaction (transition state near reactants), kinetic energy is more effective than vibrational energy at passing the transition state, and that for an endothermic reaction (transition state near products), vibrational energy is more effective than kinetic energy at passing the transition state.
Please provide references for external information. Fdp18 (talk) 19:39, 28 May 2019 (BST)
For the reaction F + H2, we can see that having vibrational energy in excess of the transition state does not necessarily result in passing the transition state, but having just enough kinetic energy to be above the transition state can cause the reaction.
For the reaction HF + H, we can see that without vibrational energy, an extremely large amount of kinetic energy is needed to cause the system to pass the transition state, but with more vibrational energy, a much lower total energy is required.