MRD:yh13018
Explanations and possible answers to the questions
Ng611 (talk) 19:03, 22 May 2020 (BST) Overall: 4/5 - Generally correct, but with one or two bits missing. I'd maybe also consider making your answers more succinct.
EXERCISE 1: H + H2 system
Question 1: On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
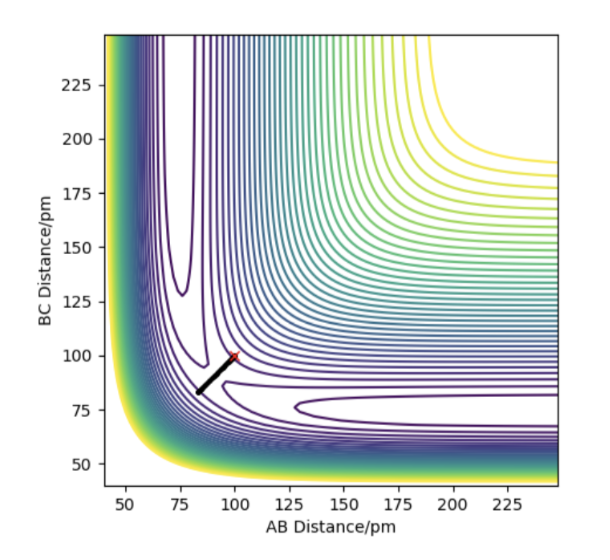
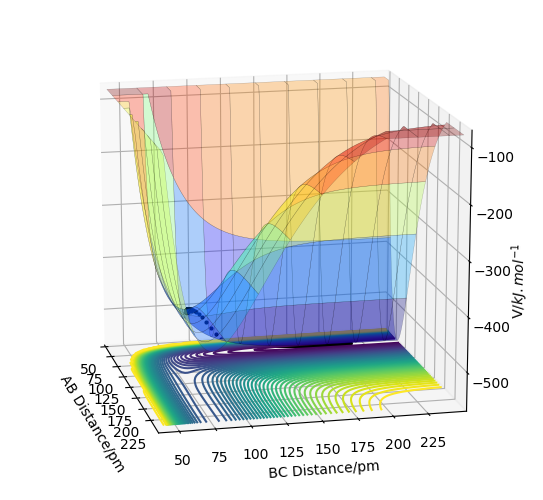
The potential energy surface (PES) above shows that when the reactant molecules are closer, the energy of the system increases, and the structure of maximum energy is the transition state. The energy then decreases until the product is formed. The transition state is the first-order saddle point on PES. It shows that the energy is maximum in one direction in this configuration space but in other directions, the energy is minimum. In this case, the gradient of the function is set to zero and the stationary point of the function might be regarded as the transition state (∂V(ri)/∂ri=0).
Firstly, saddle points generally appear in a multivariable function.In one direction, if the slope of the function is zero, (∂V(ri)/∂rAB)rBC=0 and (∂V(ri)/∂rBC)rAB=0. At the minima, both (∂^2V(ri)/∂rAB^2)rBC=>0 and (∂^2V(ri)/∂rBC^2)rAB=>0 due to the positive curvature. However, at the saddle point, (∂^2V(ri)/∂rAB^2)rBC=>0 but (∂V^2(ri)/∂rBC^2)rAB=<0 because one of the curvature is negative. Therefore, the function is differentiated first to obtain the minima and then it undergoes partial differentiation to check the curvature in different directions. If one is positive and one is negative, the saddle point is found and it is the transition state. Or if f(r1r1)-f^2(r2r2)<0, there will be a saddle point; if it is bigger than zero and f(r1r1)<0, there will be a local minimum, but if f(r1r1)>0, there will be local maximum.
All in all, minima has only positive curvature and it shows a positive partial differentiation while saddle point has both positive and negative curvature. The energy goes down along the minimum energy pathway, and if a trajectory stays on transition state with zero initial momentum, it will never fall off.
Ng611 (talk) 18:50, 22 May 2020 (BST) Your answer, whilst absolutely correct, is a bit muddled. Think about how you could distill your answer further into something a bit more concise. Otherwise, this is a good response, well done!
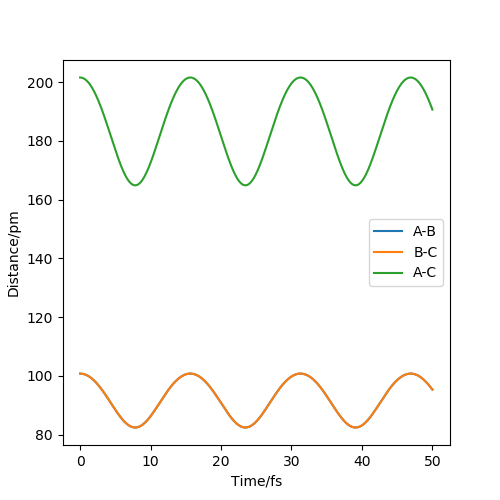
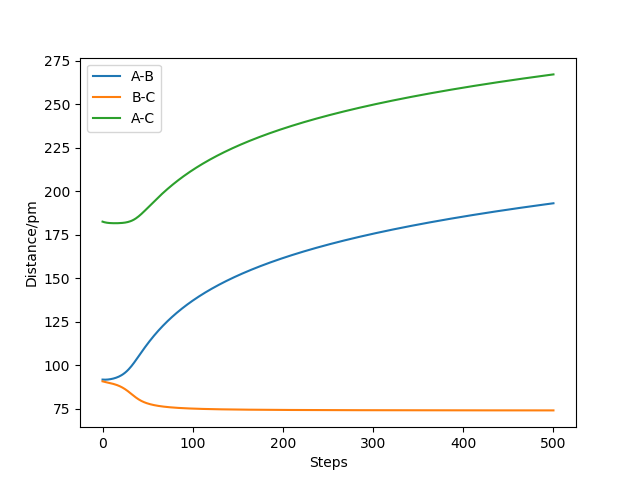
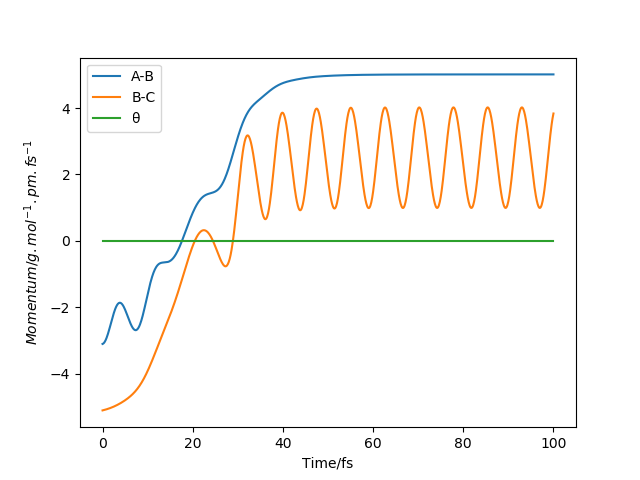
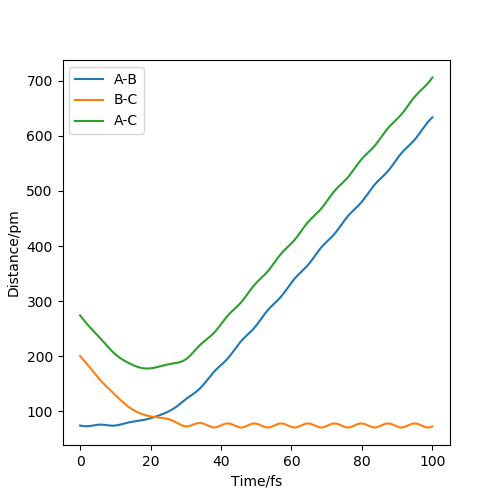
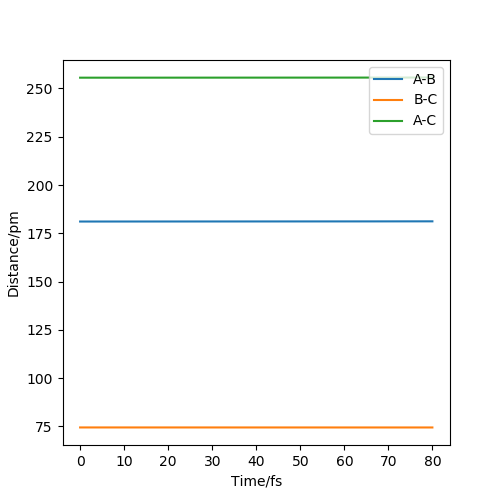
Question 2: Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
The estimate of the transition state position is about 90.8pm. The triatomic molecule is the transition state because it shows the highest energy, and in this reaction, it should be H-H-H. The trajectory which stays on the ridge is always keeping oscillating, but if it moves slightly, it will fall off. As can be seen from the three plots, when r=90.8pm, the three atoms do not move while when r=100.8pm or r=80.8pm, the largest distance that the three atoms move and the time they use is almost the same. If the distance increases slightly, the atoms will be closer first, while the atoms move further first when the distance decreases. It shows that the triatomic molecule is formed at about 90.8pm and the trajectory formed at transition state will not fall off because the gradient there is zero and it is a stationary point.
Ng611 (talk) 18:51, 22 May 2020 (BST) Excellent reasoning, and a sensible answer for the TS position. Well done!
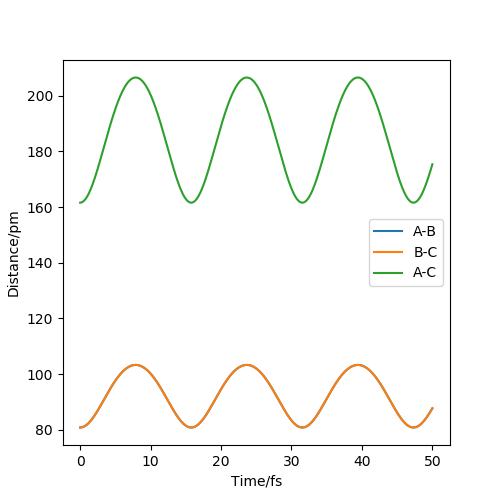
Question 3: Comment on how the mep and the trajectory you just calculated differ.
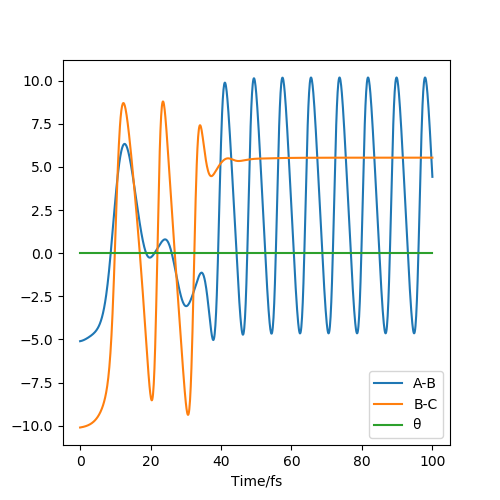
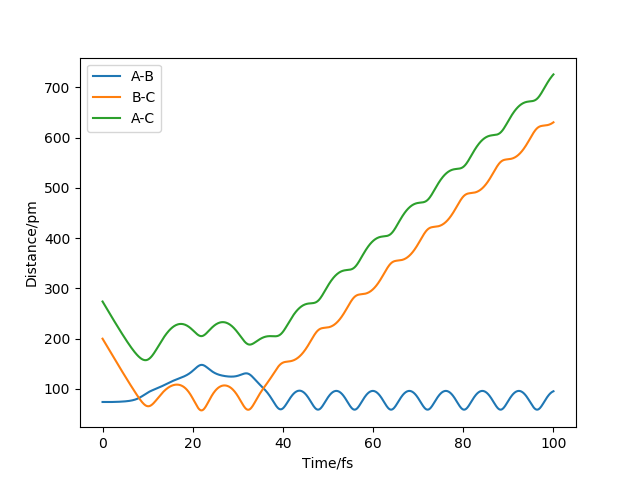
The two graphs show a dynamic trajectory and a minimum energy pathway (MEP) with the same condition which are the positions r1 = 91.8pm, r2 = 90.8pm and the momenta p1 = p2 = 0 g.mol-1.pm.fs-1. Any point on MEP is at the energy minimum in all directions perpendicular to the path. An infinitely slow motion can be achieved. From the graph above, MEP one shows that atom B and atom C become slightly closer, while atom A and atom B separate from each other and reach a relatively constant separation and zero velocity. Dynamic one shows that atom A and atom B stay reasonably stable first and then continue moving further away from each other. In this case, as we reach the zero velocity in MEP, the kinetic energy and momentum always keep zero according to KE=1/2mv^2 and p=mv. Moreover, as the distance between atom B and atom C increases compared with the transition state, the reaction pathway is prone to the product, which is BC. The dynamic graph also shows that the atoms continue vibrating because the distance between B and C is changing. However, if we use r2=91.8, the pathway will be prone to the reactant, which is AB. Other properties do not change too much. If the momenta have a different sign, the velocity will be in the opposite direction. The atoms move in different directions can determine which product is formed.
Ng611 (talk) 18:52, 22 May 2020 (BST) Good!
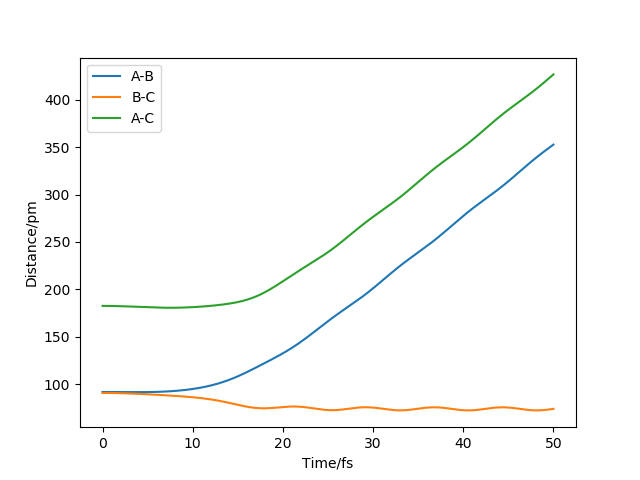
Question 4: Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?
Ng611 (talk) 18:54, 22 May 2020 (BST) These all look sensible, but a contour or surface plot would have been better as it would enable you to observe the position of the atoms relative to the TS you found?
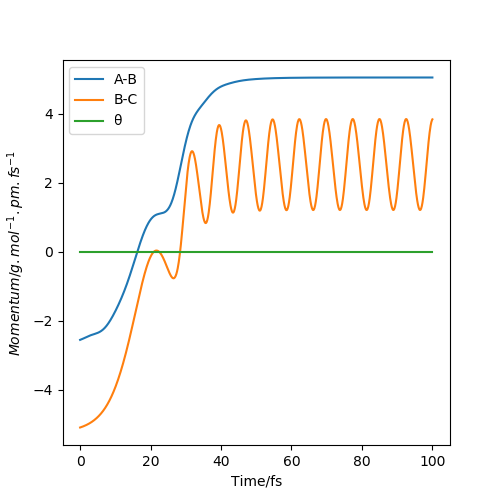
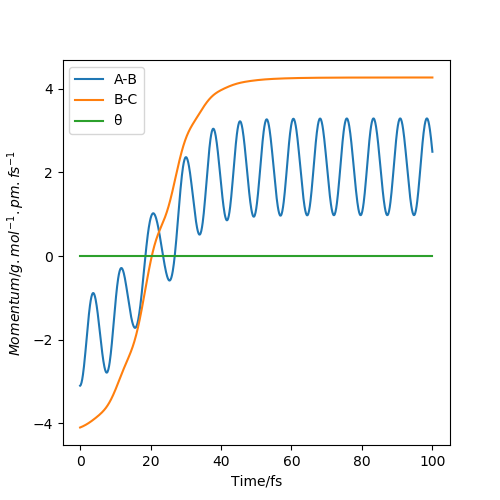
The momentum graphs show the relative momentum between atoms and the gradient is the force that the atoms experience.
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot/KJ mol-1 | Reactive? | Description of the dynamics | Illustration of the trajectory | |
|---|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.28 | Reactive |  From the graph, we can see that atom A experiences large force because it is close to B, which allows attraction present. However, the force continues decreasing because atom moves further away from both B and C, and finally the force becomes zero and the momentum is constant. The change in sign means that atom A moves to the opposite direction. The atom C experiences low force at first as it is further away from AB, but the interaction goes up later. When BC is formed, the momentum is always changing because the two atoms are vibrating. They undergo attraction if they move slightly further away and they experience repulsion if they are too close. The change in sign also shows that atom C moves to opposite directions. The velocity can also be analysed. When BC is formed at about 30fs, atom A moves faster than both atom B and atom C which both have similar velocity. The positive sign of the relative velocity means that atom A and atom B move in different directions, while atom B and atom C are oscillating so the direction of movement keeps changing.
|
Initially, A and B are closer together while B and C are further. A and B move to C, which allows BC to form and A to continue moving away. All atoms are vibrating.|| | |
| -3.1 | -4.1 | -420.077 | Uneactive |  The reaction do not happen thus no BC is formed. The atom C moves closer to AB first but the KE and the attraction are not high enough to allow the interaction between B and C to form. In this case, atom C moves further away from AB after about 20fs. The force between atom C and AB continues going down until disappearing, thus the momentum is constant after about 40fs. The force between atom A and atom B is always changing from repulsion to attraction and changing back so there is an oscillation. The atom C has the largest velocity when they move further away, and the positive relative velocity shows that the distance between atom C and AB increases, vice versa. |
 It is unreactive so no product is formed. The separation between A and B is reasonably constant but C continue moving further away from both A and B. |
|
| -3.1 | -5.1 | -413.977 | Reactive |  The situation is similar to the first one. The difference is the initial momentum used, which causes the atom A and atom B to oscillate slightly before they approach atom C. Because the higher KE contributes to the higher energy of the atoms. In this case, the velocity varies as well. |
 A and B are closer initially and they move together closer to C. The product BC is formed, which shows that A keeps moving away. It shows a smooth motion. |
|
| -5.1 | -10.1 | -357.277 | Reactive |  The much higher momentum means that more KE is provided for atoms to oscillate. In this case, when three atoms are close together, the oscillation happens between all of them. The force between atom A and atom B goes down initially thus the force between atom B and atom C is higher. However, the KE does not allow the stable force to exist between atom B and atom C. The atom C moves away from AB. The force between atom A and atom B varies significantly and the distance between them changes a lot during oscillation. Because the KE is relatively large, which causes distablisation of the atoms. Finally, the reactant is reverted back. |
 The final product is AB but before about 40fs, the distance between B and C is smaller and BC is formed. However, B and C are vibrating relatively vigorously and finally A and B approach to each other |
|
| -5.1 | -10.6 | -349.477 | Reactive |  It has the similar situation as the one above. The system crosses the transition state region, thus once the product BC is formed, the reactant AB is prone to form again because the force between atom A and atom B increases, and the energy is not stable. The product BC is formed in this case. The oscillation is relatively large and the atom which is far away experience zero force. |
 It has a similar situation with the one above but finally BC is formed. B vibrates between A and C so it approaches C first and after one oscillation, B and C move away from A.
|
Conclusion: 1. When two atoms are close together, they are oscillating. If they are too close, there will be a repulsion; if they are slightly further away, there will be an attraction. The higher the KE, the stronger the oscillation. 2. A reaction can not happen without enough energy. However, if the KE is out of a specific range, the products and reactants will be unstable, which may contribute to the barrier recrossing. 3. The atom which is far away from the other two atoms experience zero forces, which leads to constant momentum. 4. The lower value of kinetic energy is still able to overcome the potential energy.
Question 5: Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Compared with experimental result, transition state theory might overestimate rate values. Transition state theory assumes that the transition state structure does not go back to the reactants once the transition state is formed and an equilibrium is present between reactant and transition state. In this case, it ignores the effect from barrier recrossing.
However, the theory is treated classically, and thus the tunneling effect, which is the quantum mechanical phenomenon, is ignored. In this case, particle with lower kinetic energy is able to overcome the higher potential energy in experimental values. Transition state theory may underestimate the rate because it requires more energy and higher barrier.
Ng611 (talk) 18:55, 22 May 2020 (BST) Both tunelling and TS recrossing both represent deficiencies of TS theory, however, TS recrossin is far more significant than tunelling.
EXERCISE 2: F - H - H system
Question 6: By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The initial conditions of the PES are rFH=150 pm and rHH=80pm at minimum energy pathway. It clearly shows that when the distance between H and F decreases and the distance between H and H increases, the energy is lower, which is more negative. In order to form HF in the F+H2 reaction, the energy is released, which is exothermic. If the distance between F and H decreases and the distance between H atoms goes up, relatively higher energy is needed to absorb, thus HF + H reaction is endothermic. An exothermic means that the energy of bond-forming is higher than that of bond breaking, in this case, the energy needed to form HF is higher than the energy to break H2. For another reaction which is endothermic, the energy of the formation of H2 is lower than the energy of breaking HF. In conclusion, the bond strength of H2 is higher than that of HF.
Ng611 (talk) 18:55, 22 May 2020 (BST) Excellent!
question 7: Locate the approximate position of the transition state
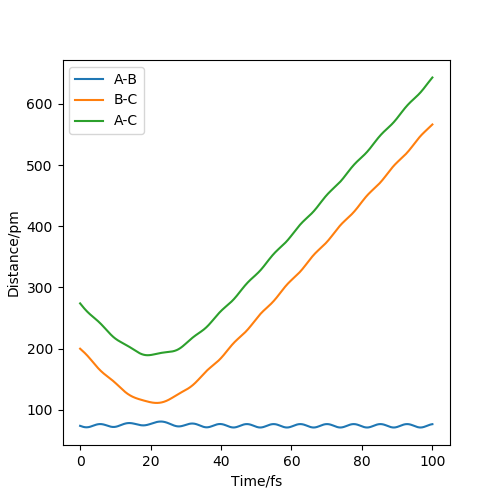
The transition state estimated is at about rFH=74.5pm and rHH=181.1pm. Hammond postulate implies that the transition state is closer to the reactants than to the products in energy In an exothermic reaction, and vice versa. Therefore the transition state is prone to the H2 and F, thus the distance between H atoms is relatively small. From the graph, we can see that the three atomic molecule is formed and no product or reactant is present. When potential energy goes up, the product (HF) is formed and vice versa.
Ng611 (talk) 18:56, 22 May 2020 (BST) A good estimate and a sensible piece of evidence provided, well done! How did you confirm this was a TS and not an energetic minimum?
question 8: Report the activation energy for both reactions.
The activation of F+H2 reaction is about 1.12 KJ mol-1 and the activation energy of HF+H reaction is about 126.424KJ mol-1. The first plot of energy shows the potential energy as well as the total energy of the reactant(F+H2), and the second plot shows the one of the product(HF+H). The activation energy is the energy that the reactant needed to overcome so that the reaction can happen. It is the difference between the potential energy of transition state and their initial state.
Ng611 (talk) 18:57, 22 May 2020 (BST) Excellent responses and correct estimates, well done!
question 9: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
The initial condition set is rHF=190pm and rHH=74 for F+H2 reaction. It is an exothermic reaction thus the energy released for foming HF. From the first graph, the momentum is set at pHF=-0.1g.mol-1.pm.fs-1 and pHH=-1.1g.mol-1.pm.fs-1. It is obvious that the HF is not formed and the kinetic energy is only about +1.105KJ mol-1, which shows that not so much potential energy is transfered to kinetic energy. However, in the second graph, the activation energy is overcomed and HF is formed. The momentum now is pHF=-0.1g.mol-1.pm.fs-1 and pHH=-20g.mol-1.pm.fs-1. More potential energy is transfered to kinetic energy, which is about +398.005KJ mol-1. In conclusion, when the HF bond is formed, the energy released shows that potential energe is transfered to kinetic energy. Moreover, temperature is the average kinetic energy, in this case, the increase in kinetic energy can be proved by the increase in temperature. We can use calorimetry to investigate the change in temperature during reaction.
Ng611 (talk) 18:59, 22 May 2020 (BST) Calorimetry is insensitive to whether energy is released as translational or vibrational energy though. Can you think of a method that is sensitive to this difference?
question 10: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Translational energy is due to the change in the locations of atoms or molecules and vibrational energy is from the change in the shape of molecule, like stretching and bending. The rate of reaction can sometimes be detemined by the properties of transition state. Transition state is always located close to the top of a potential barrier, which requires high energy to overcome it. Translational energy and vibrational energy have the influence on the rate of the reaction, which often depends on the position of transition state. The translational energy is more effective than vibrational energy when there is a reactant-like transition state, while the vibrational energy will be more effective if a transtion state is closer to the product. Generally, an exothermic reaction gives the reactant-like transition state and thus higher kinetic energy, which can comes from the energy chaning in position or location. Moreover, symmetric vibration sometimes has higher rate and reactivity than antisymmetry vibration.
Ng611 (talk) 19:01, 22 May 2020 (BST) Again, correct answer but somewhat unclear in your explanation. You also needed to provide some examples to back up your assertions here as well.