Reaction of H + H-H

Examining the Potential Energy Surface

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The total gradient is zero at the minima and at the transition state. This is because at a minimum point the gradient should be zero. The transition state is the maximum value on the minimum energy path, therefore it should also have a gradient of zero (gradient at a maximum point is zero). We can distinguish the minimum structure from the transition structure by examining the value of the minimum point. At the minimum energy structure, the potential energy is at its lowest, for a fixed distance r₁or r₂,but there exists higher values than the minimum energy value, of which the transition structure has the highest energy value.

(This paragraph is quite hard to follow... Tam10 (talk) 15:20, 1 June 2017 (BST))

As seen from the above images, by viewing the potential surface from another angle, we can see where the transition state is located. The PES has the shape of a "mountain pass" ^[1], with the channel representing the transition from reactants to products. The leftmost and bottom edges represent the potential energy when two or three of the particles become very close to each other, and the flat surface to the top right of the PES shows the potential energy when the three particles have dissociated.^[2]

The point where the transition state is located is known as a saddle point. If a point is a saddle point, it satisfies the conditions that: $\frac{\partial E}{\partial {r_{A}}_{B}} = 0$ , $\frac{\partial E}{\partial {r_{B}}_{C}} = 0$ and $\frac{\partial^{2} E}{\partial^{2} {r_{A}}_{B}} \frac{\partial^{2} E}{\partial^{2} {r_{B}}_{C}} - \frac{\partial^{2} E}{\partial {r_{A}}_{B} \partial {r_{B}}_{C}} < 0$ .

Locating the transition state

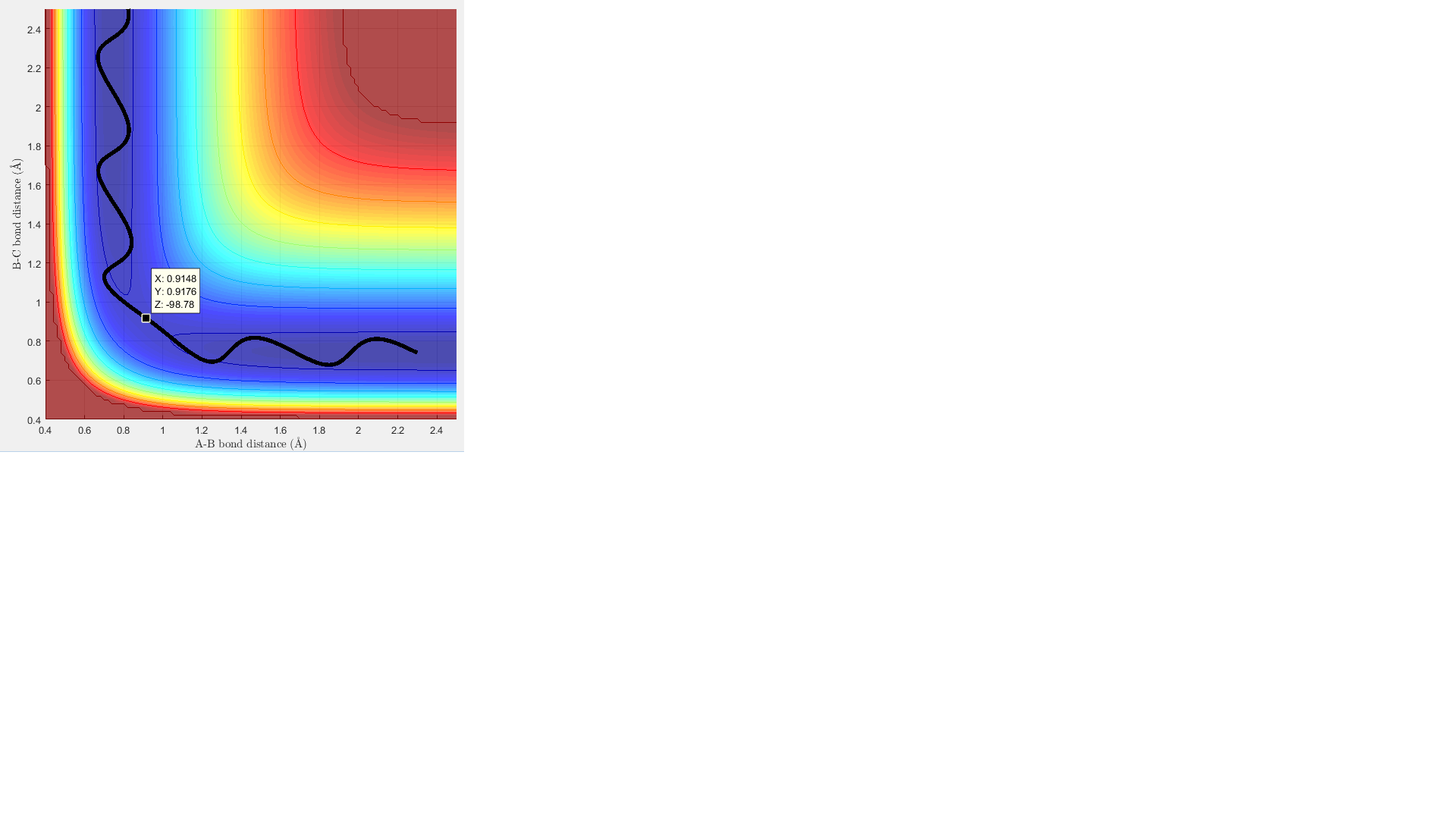
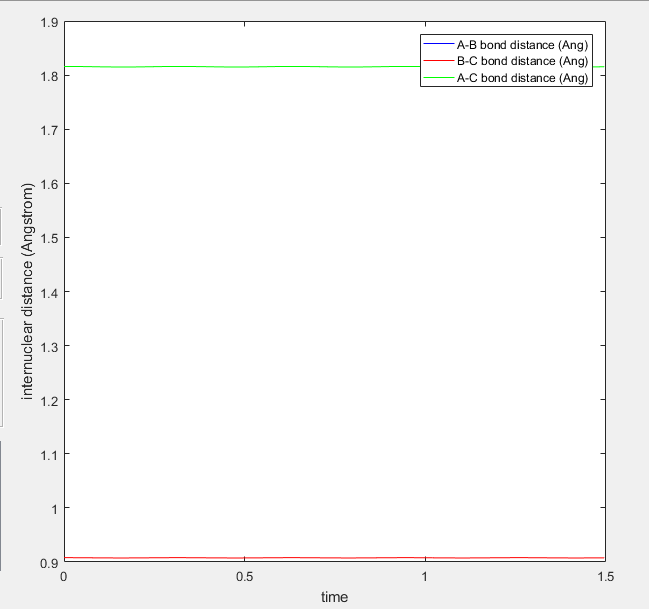
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

The transition state energy value is estimated to be r= 0.908 Å. Since the transition state is a path maximum, the internuclear distances should not oscillate. This is shown by the lines on the internuclear distance over time plot, which are nearly flat.

Examining the MEP

Comment on how the mep and the trajectory you just calculated differ.

The mep shows the particle to have only travelled a short distance. There is no vibration of the newly formed hydrogen molecule. The dynamics trajectory shows both the escape of particle A and vibration of the newly formed particle BC. This is because the mep sets the momentum of the particles to zero after each iteration. This means the reaction will always take the lowest energy path. In the case of the dynamics calculation, the particles gain energy as the reaction proceeds, this allows it to travel up the slope of the potential surface, and therefore to oscillate.

When the bond distances and momentum is swapped, the same reaction path appears, but this time it is rotated, as the reacting particles will collide and travel in the opposite direction compared to before.

Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory

Reaction No.	p₁	p₂	outcome
1	-1.25	-2.5	reactive
2	-1.5	-2.0	not reactive
3	-1.5	-2.5	reactive
4	-2.5	-5.0	not reactive
5	-2.5	-5.2	reactive

(This does NOT match what you have below... You must report what you see, not what other people have said. Tam10 (talk) 15:20, 1 June 2017 (BST))

We can deduce the outcome of a reaction by looking at the contour plot for the PES. If the reaction occurs, the path traveled goes through the blue channel. If the reaction does not occur, it will travel some distance into the blue channel, and then move back. The images below show the path taken by the reactions with different momenta in the order presented.

(You have started in the wrong place, but worse, you have swapped P_AB and P_BC. There is no discussion or mention of Transition State Theory Tam10 (talk) 15:20, 1 June 2017 (BST))

Reaction of F + H-H

Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

F+H₂ is exothermic, because the bond enthalpy for the H-H bond is lower than that for the H-F bond. The reaction H+HF is endothermic, because the H-F bond is broken this time, so less energy is released than is taken in. The H-F bond is stronger than the H-H bond.

Finding the transition state

Locate the approximate position of the transition state. For the reaction F+H-H, the transition state occurs at a position with the following bond distances.

F-H: 1.82 Å

H-H: 0.74 Å

For H+H-F,

H-H:0.74 Å

H-F:1.82 Å

The transition state (TS) can be located with the help of Hammond's postulate, which states that for an early transition state the appearance of the TS resembles that of the reactants, whereas a late transition state would resemble more the products. An exothermic reaction will have an early TS, an endothermic reaction will have a late TS. Therefore, we would expect the bond distances for the FH₂ reaction to have bond lengths similar to that of a separated fluorine atom and H-H bond, whilst the bond distances for the HFH reaction to be similar to that of two FH bonds.

Report the activation energy for both reactions.

in kcal/mol

F+H-H: 103.3

H+F-H: 103.3

(No, this is the TS energy. Tam10 (talk) 15:20, 1 June 2017 (BST))

Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

A set of conditions which results in a reaction are as follows.

Atoms	Distance (Å)	Momenta
F, H	2	-3
H, H	0.74	2

The animation shows a new bond being formed between the F and H atoms, and the H-H bond being broken. In this reaction energy can be either kinetic energy, or potential energy. The total amount of energy should remain constant. Looking at the animation, the fluorine atom approaches the hydrogen molecule. As it moves closer the hydrogen at at the end moves away, whilst fluorine approaches. The F-H atom eventually ends up oscillating, at which point we can be sure a new bond has formed. The internuclear momenta vs time graph shows the momentum between F and H to go through a dip, before oscillating at a constant frequency, whilst the momentum between the two hydrogen atoms remain constant after a change of sign at the beginning. In order to go through a change of sign in the momentum, there must be a point at which the momentum is zero. Therefore the kinetic energy will also be zero at that time. There is no movement at that point in time, which suggests the presence of a force which decelerates the atoms. This implies the energy is likely to have been converted to the form of potential energy. A further graph of kinetic energy over time demonstrates the loss of kinetic energy.

Overall what happens is as the molecules approach each other, kinetic energy is converted into potential energy as the atoms interact and repel each other. The kinetic energy decreases as the molecule travels through the transition state. However, once the new bond is formed, the newly made molecule oscillates at a different frequeny, and we see a reconversion of potential energy to kinetic energy. The trajectory across the PES also supports this, since in order to arrive at the transition state the atoms have to reach the reaction path maximum, representing a gain in potential energy.

Experimentally, we can use the technique of IR spectroscopy to confirm the release of reaction energy. Since initially the H-H molecule is IR-inactive, the absorption which appears will be due to the H-F bond vibration. This confirms the formation of a new bond.

(This doesn't demonstrate a change in energy however. Tam10 (talk) 15:20, 1 June 2017 (BST))

Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well r_HH = 0.74, with a momentum p_FH = -0.5, and explore several values of p_HH in the range -3 to 3 (explore values also close to these limits). What do you observe?

The initial conditions used were

FH distance: 2Å, HH distance: 0.74Å. p_FH: -0.5

There is no simple relationship between the momentum and whether or not a particle will react. The path travelled by the reaction changes with incremental change in momentum. When the momentum value is close to zero, the corresponding path also decreases in amplitude of oscillation. This can be explained by the lower kinetic energy possessed by the particle in the beginning.

For the same initial position, increase slightly the momentum p_FH = -0.8, and considerably reduce the overall energy of the system by reducing the momentum p_HH = 0.1. What do you observe now?

What happens now is the reactant travels down the product channel, but due to the high amplitude of bond vibration after the products are formed, it reacts again in reverse and ends up in the product channel again.

Polanyi's rule

Setup initial conditions starting at the bottom of the entry channel, with very low vibrational motion on on the H - F bond, and an arbitrarily high value of p_HH above the activation energy (an H atom colliding with a high kinetic energy). Try to obtain a reactive trajectory by decreasing the momentum of the incoming H atom and increasing the energy of the H - F vibration. The cases studied are an illustration of Polanyi's empirical rules. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's rule state that: For a late transition state reaction vibrational energy is more efficient in promoting the reaction than translational energy. For a early transition state reaction translational energy is more efficient in promoting the reaction than vibrational energy. ^[3] Since the reaction concerned has a late transition state, we do not expect the initial conditions will allow the reaction to occur. As we gradually increase the momentum of the F-H molecule and decrease that of the H atom, the colliding atom's translational energy is decreased, whilst the vibrational energy of the molecule is increased. This ensures we will eventually reach a point where the conditions are favourable for the reaction to proceed.

References

↑ R.D.Levine, "Molecular Reaction Dynamics", Cambridge University Press, 2005
↑ R.D.Levine, "Molecular Reaction Dynamics", Cambridge University Press, 2005
↑ Zhang Z. et al, "Theoretical Study of the Validity of the Polanyi Rules for the Late Barrier Cl + CHD3 Reaction", J. Phys. Chem. Letters, 6/11/2012

[1] R.D.Levine, "Molecular Reaction Dynamics", Cambridge University Press, 2005

[2] R.D.Levine, "Molecular Reaction Dynamics", Cambridge University Press, 2005

[3] Zhang Z. et al, "Theoretical Study of the Validity of the Polanyi Rules for the Late Barrier Cl + CHD3 Reaction", J. Phys. Chem. Letters, 6/11/2012

[1]

[2]

[3]