(Fv611 (talk) 15:00, 14 June 2017 (BST) Be careful, there are many typos in your work)

Introduction

In this lab, the reactivity of triatomics systems where the linear collisions between a diatomic molecule and an atom was investigated through calculating Molecular Dynamics trajectories. Assumption was made that the motions of all atoms researched in the lab period obeyed the classical mechanics. Concepts like transition states, reaction coordinates and potential energy surfaces were studied and was employed to explain the behavior of the systems. With the variation in the atomic types, internuclear distances between the atoms and the corresponding internuclear momentum, the dynamic trajectories of the molecules and the reaction path with the lowest energy were monitored using the potential surface energy graphs, which were obtained using Matlab.

Investigated systems

1) H + H₂ system

In this collision, an atom of H (H_A) hits a molecule of hydrogen (H_B-H_C) to produce a new H_A-H_B molecule, leaving the H_C atom separated.

Dynamics from the transition state region

As the reaction proceeds, the gradient of the potential energy against the bond distance reaches zero at two points, one the minimum and the other the transition state structure, which by definition is the maximum on the minimum energy path linking reactants and the products. Although the first derivation (i.e. the gradient of the plot) is the same for the two points, the second derivation can be used to distiguish the minima and the transition state structures. As the minimum is the lowest point on the potential energy surface and is in a stable equalibrium, the second derivative of potential energy (V(r_i)) against the bond distance (r_i) would be positive. The transition state, on the other hand, possesses the highest energy and is in an unstable equalibrium. The second derivative of the trasition state structure is therefore a negative value.

(Fv611 (talk) 15:00, 14 June 2017 (BST) Ok, but (as you've stated) the TS is only a maximum in the reaction coordinate, therefore it's second derivative will be negative only in that direction)

Best estimate of the transition state position (r_ts)

The The positions of the transition state always land in the most symmetrical structurepo of the system. As the three atoms in this system are all identical, it is assumed that the transition state is located to at the point where the two internuclear distances share the same value. (i.e. r_AB=r_BC).

Since the transition state is in an equalibrium, the internuclear distance of the system stays constant when the momentum is given as zero. Also, by applying the bond length of H-H bond (0.74A) to the internuclear distances, the maximum of the path with lowest energy shows that the internuclear distance at transition state is 0.9076A.

(Fv611 (talk) 15:00, 14 June 2017 (BST) "Most symmetrical structure of the system" doesn't mean anything. The TS is only symmetrical if reactants and products are the same.)

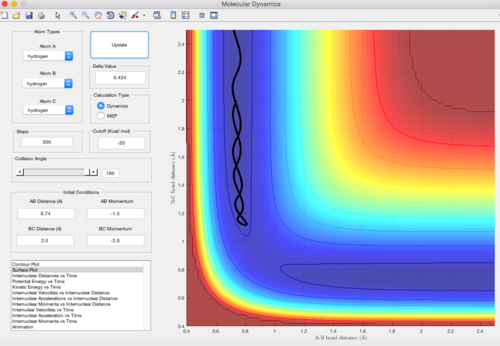
Calculation of the reaction path

The initial conditions are set as that the system is slightly displaced from the transition state and zero initial momenta (i.e. the positions r_BC = r_ts+0.01, r_AB = r_ts and the momenta p_AB = p_BC = 0). The reaction trajectories are run in both MEP and Dynamic modes.

The surface plot of H+H2 System under dynaimcs mode	The surface plot of H+H2 System under MEP mode

As shown in the two graphs above, the MEP mode gives a smooth line and the dynamic mode gives a wavy curve. This is because the dynamic mode accounts for both the transitional and vibrational motion and gives a more realistic oscillating curve. However, the MEP mode does not include the vibration inbetween the atoms, for the velocity is always reset back to zero in each time step.

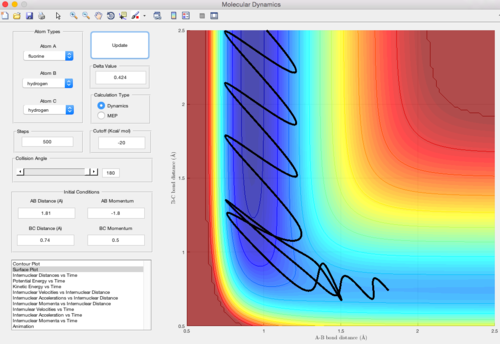
The surface plot where r_AB = r_ts+0.01, r_BC = r_ts using dynamic mode calculation is shown below. It is clear that the y=x line is the symmetric axis for the r_AB = r_ts+0.01 plot and the r_BC = r_ts+0.01 plot. The difference between the two plots is only to exchange the value of the internuclear distances (the momentum stays zero). Consequencely, the trajectory goes in the direction of the reactants and the two plots share the identical shape with inverted axises.

The surface plot of H+H2 System under dynaimcs mode with r_AB = r_ts+0.01

Reactive and Unreactive Trajectories

From the previous calculations it can be concluded that trajectories with initial conditions in the range r_AB = 0.74, r_BC = 2.0, with -1.5 < p_AB < -0.8 and p_BC = -2.5 are reactive. It would seem fair to assume that all trajectories starting with the same positions but with higher values of momenta (higher kinetic energy) would be reactive, as they have enough kinetic energy to overcome the activation barrier. Several trajectories with different momenta combinations are run to test the hypothesis. The initial positions r_AB=0.74 and r_BC=2.0.

Trajectory 1


p_AB = -1.25 p_BC = -2.5	Reactive
The internuclear dis of H+H2 System under dynamics mode with p_AB=-1.25 p_BC=-2.5	The surface plot of H+H2 System under dynamics mode with p_AB=-1.25 p_BC=-2.5

In this trajectory, p_BC is large enough to provide enough kinetic energy to overcome the reaction activation energy, so the H_A atom approaches properly and a new H_A - H_B bond is formed.

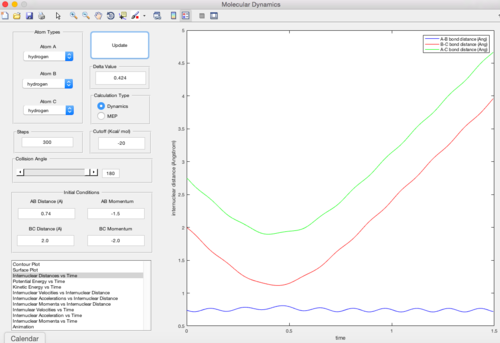
Trajectory 2


p_AB = -1.5 p_BC = -2.0	Unreactive
The internuclear dis of H+H2 System under dynamics mode with p_AB=-1.5 p_BC=-2.0	The surface plot of H+H2 System under dynamics mode with p_AB=-1.5 p_BC=-2.0

In this trajectory, p_BC is not large enough to provide enough kinetic energy to overcome the reaction activation energy, so the H_A atom approaches the transition state but reverts vack before the formation of product.

Trajectory 3


p_AB = -1.5 p_BC = -2.5	Reactive
The internuclear dis of H+H2 System under dynamics mode with p_AB=-1.5 p_BC=-2.5	The surface plot of H+H2 System under dynamics mode with p_AB=-1.5 p_BC=-2.5

In this trajectory, p_BC is large enough to provide enough kinetic energy to overcome the reaction activation energy, breaking the H_B - H_C bond and forming a new bond. It has the similar pattern as in trajectory 1.

Trajectory 4


p_AB = -2.5 p_BC = -5	Unreactive
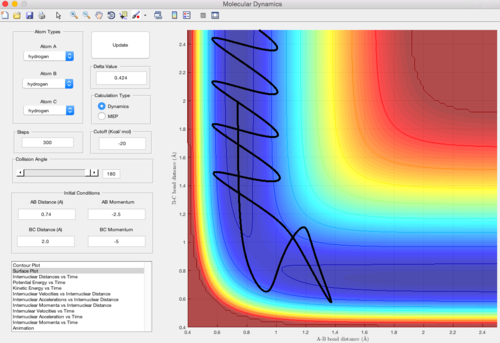The internuclear dis of H+H2 System under dynamics mode with p_AB=-2.5 p_BC=-5	The surface plot of H+H2 System under dynamics mode with p_AB=-2.5 p_BC=-5

In this trajectory, p_BC is large enough to overcome the reaction activation energy but barrier recrossing occurs. The energy is not enough to overcome the reaction activation energy once more to form the product. Therefore, the reactans are reformed.

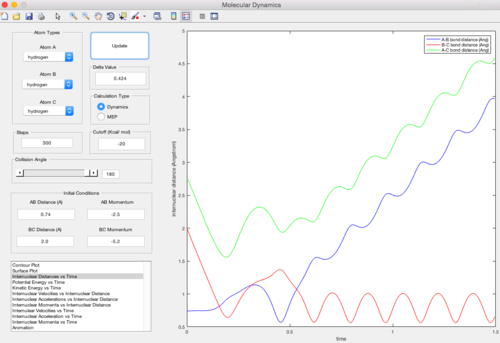
Trajectory 5


p_AB = -2.5 p_BC = -5.2	Reactive
The internuclear dis of H+H2 System under dynamics mode with p_AB=-2.5 p_BC=-5.2	The surface plot of H+H2 System under dynamics mode with p_AB=-2.5 p_BC=-5.2

In this trajectory, p_BC is large enough to overcome the reaction activation energy twice. Barrier recrossing occurs and the system overcomes the reaction activation energy again to form the final product.

(Fv611 (talk) 15:00, 14 June 2017 (BST) Ok, but you could have discussed more. For example, how are trajectory 1 and 3 different?)

Transition state theory

In the transition state theory, assumption is made that in the reaction equilibrium, the reaction can only proceed in the direaction of the product once the activated transition state complex is formed, which means it is not possible for the reaction complex to recross or revert back to the reactants, let alone regenerating the products. However, this have been proved to be actually possible in trajectory 5, where the predicted minimum energy path is replaced by another experimental path. The transition state theory, in other words, is not supported by the experimental data.

(Fv611 (talk) 15:00, 14 June 2017 (BST) This is a good point, but you are overlooking a huge detail of TST: how does it deal with describing quantum effects? Also, you do not discuss how the rates predicted by TST would compare to experimental ones.)

2) F - H - H system

There are two types of possible collisions in this system. One is that an atom of F hits a molecule of hydrogen (H_A - H_B) to produce a new F-H_A molecule, leaving the H_B atom separated. The other is that an atom of H_B hits a molecule of H_AF to produce a new H_A - H_B molecule, leaving the F atom separated. The bond strength of H-F bond is significantly large, for the electronegativity difference between H and F is large and bond is fairly polar with the large ionic character. As the H-H bond is much weaker than the H-F bond, the energy required when the H-H breaks is much less than that released when the new H-F bond forms. Consequently, the F + H₂ reaction is exothermic. As the HF + H reaction can be seen as the reserve reaction of F + H₂, it is endothermic.

(Fv611 (talk) 15:00, 14 June 2017 (BST) Would have been better to relate the energy of reaction to the shape of the potential energy surface.)

According to Hammond's Postulate, if a transition state and an unstable intermediate, occur consecutively during a reaction process and have nearly the same energy content, their interconversion will involve only a small reorganization of the molecular structures. In other word, the transition state would resemble the one of the reactant and product with a smaller energy gap. In the exothermic F + H₂ reaction, the transition state complex will resemble the reactants, which leads to a relatively small reaction activation energy; while in the endothermic HF + H reaction, the transition state complex will resemble the products, resulting in a larger reaction activation energy.

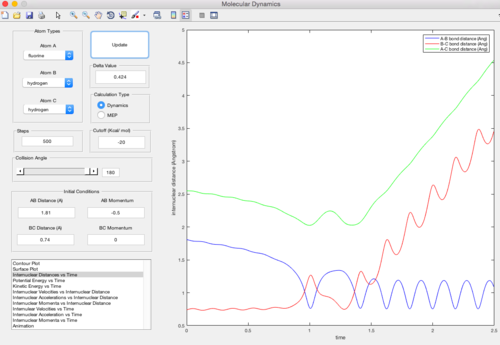
F + H₂ : As illustrated above, the transition state resembles the reactants both in energy and in structure and will be located at the position where if no momentum is given, it will remain at the position and the internuclear position will remain constant.

The internuclear distance stays constant at transition state with 0 momentum.

The transition state is discovered at the position where the distance between H atoms as 0.745 A and the distance between H and F as 1.81 A. The H-H distance is slightly longer than the H-H bond distance (0.74) A.

The point on the potential energy curve represents the transition state.	coordinates of the transition state

The activation energy is determined by the energy difference of the transition state and the reactants, which in this case was very small of around 0.2 kcal/mol.

The energy for the reactants.	The energy for the transition state

H + HF : The transition state resemble the product and will be located near the position of products on the potential energy curve.

The point on the potential energy curve represents the transition state.	coordinates of the transition state

The transition state is located at the position where the internuclear distance of H and H AB=1.81 Å and the internuclear distance of H-F BC=0.7465 Å.

The energy for the reactants.	The energy for the transition state

The activation energy in this endothermix reaction is 30.1 kcal/mol.

Reaction dynamics

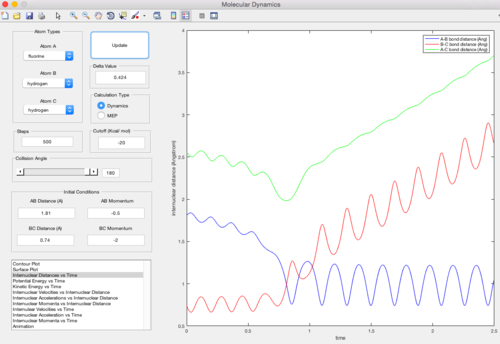
Mechanism for the F+ H2 system. The set of initial conditions that results in a reactive trajectory is set as: r_FH=1.81 Å, r_HH=0.74 Å, p_FH=-1.8 kgms^-1, p_HH=0.5 kgms^-1

The surfance plot for a reactive trajectory of F+ H₂	The internuclear momentua vs time plot for a reactive trajectory of F+ H₂.
The potential energy vs time plot for a reactive trajectory of F+ H₂	The kinetic energy vs time plot for a reactive trajectory of F+ H₂.

The mechanism of the reaction can be divided into two steps. Initially the F atom (negative momentum) approaches the vibrating H₂, attacking the H_A atom in the middle, which is shown by the oscillating values of the internuclear momentum. The second step is the dissociation of the H-H bond and the generation of H-F bond. The increasing extent of oscillation fo B-C internuclear momenta indicates that the bond is elongated and the fluctuation decreases afterwords, which indicates that the H-H bond breaks thoroughly and the H_B atom goes away from the newly formed H_AF molecule. The oscillation of A-B internuclear momentum is the direct proof of the formation and the vibration of H_AF molecule. As the energy is always conserved, the potential energy is converted to kinetic erengy in this reaction. The sligtly fluctuated curve in both kinetic energy vs time plot and potential energy vs time plot indicates that there are minor vibrations of the reactants. The energy is converted between the two types of energy and is mainly potential energy. With the exothermic nature of the reaction, the reactantshas much larger potential energy than that of the products, which results in the massive convertion from potential energy to kinetic energy during the reaction process. The vibration of H-F bond is more significant than the H-H bond. As an experimental confirming method, IR spectroscopy is suggested to check the reaction as it monitors the vibration of the bonds in the molecules.

Momentum and Trajectory

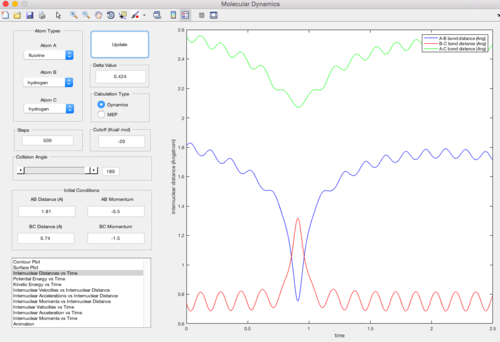
The internuclear momentum of H-H is set as the variation, the range is inbetween -3-3 kg m s^-1. The two internuclear distances and the internuclear momentum of F-H remains constant with the values of: r_FH=1.81 Å, r_HH=0.74 Å, p_FH=-0.5 kgms^-1.

Internuclear distance vs time with p_HH= -3kgms^-1. UNREACTIVE.	Internuclear distance vs time with p_HH= 3kgms^-1. UNREACTIVE.
Internuclear distance vs time with p_HH= -2.5kgms^-1.UNREACTIVE.	Internuclear distance vs time with p_HH=2.5kgms^-1. REACTIVE.
Internuclear distance vs time with p_HH=-2kgms^-1. REACTIVE.	Internuclear distance vs time with p_HH= 2kgms^-1. UNREACTIVE.
Internuclear distance vs time with p_HH= -1.5kgms^-1. UNREACTIVE.	Internuclear distance vs time with p_HH= 1.5kgms^-1. UNREACTIVE.
Internuclear distance vs time with p_HH= -1kgms^-1. UNREACTIVE.	Internuclear distance vs time with p_HH=1kgms^-1. UNREACTIVE.
Internuclear distance vs time with p_HH=-0.5kgms^-1. UNREACTIVE.	Internuclear distance vs time with p_HH= 0.5kgms^-1. UNREACTIVE.

Internuclear distance vs time with p_HH= 0. REACTIVE.

Only the ones with p_HH = -2, 0, 2.5kgms^-1 are reactive. Since the reaction activation energy of F + H₂ is relatively small, the activation barrier is expected to be easy to overcome and the trajectories should always be reactive. However, the experimental data gives the different answer: only certain values of p_HH can give a reactive trajectory. In this reaction, it could be observed that in the reactive trajectory,the reactants have low vibrational kinetic energy which react in a exothermic reaction to give product with high vibrational kinetic energy.

H + HF system

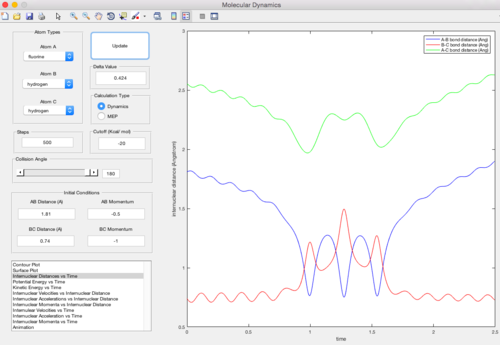
A reactive trajectory for the H + HF system.	An unreactive trajectory for the H + HF system.

It is stated in the Polyanyi's empirical rule that the vibrational energy is more effective in promoting the late barrier than the translational energy. As an endothermic reaction, the H+HF system has a late barrier and it is expected to obey the Polyanyi's empirical rule. When the vibrational energy is low in the above trajectory, it does not react as according to the rules. The reaction proceeds only with high intermolecular momenta and high vibrational energy. In the surface plot of reactive trajectory, the momentum of HF bond is set as much larger than the momentum of HH bond, which gives rise to the large vibrational energy for the HF molecule. Therefore, the reacion trajectories obey the Polanyi's rules.

Referrence

[1] P. W. Atkins, Atkins physical chemistry, Oxford University Press, Oxford, 2014.

[2] I. N. Levine, Physical Chemistry, McGraw-Hill, Auckland, 1978.

[3] ROBERT J. SILBEY, ROBERT A. ALBERTY, MOUNGI G. BAWENDI, PHYSICAL CHEMISTRY, JOHN WILEY & SONS INC, S.l., 2004.

[4] R. D. Levine, Molecular reaction dynamics, Cambridge University Press, New York, 2005.