MRD:xlt15
Molecular Reaction Dynamics: Applications to Triatomic Systems
Reaction 1: H + H2 Atom-Diatomic System
The system studied are composed of diatomic H2 molecule, HBHC and a hydrogen atom, HA. The distance in molecule HBHC is denoted by r1 or rBC. The inter-fragment distance between HA atom and HBHC molecule is denoted by r2 or rAB.
The conditions are initially set as below to run and visualize a trajectory:
rBC = 0.74 Å, rAB = 2.30 Å
p1 or pBC = 0, p2 or pBC = -2.7 Ns
Dynamics from Transition State Region
The total gradients (first derivative) of the potential energy surface are both 0 at minimum and at a transition state. Since transition state is defined as the maximum on the minimum energy path linking reactants and products, the second derivative for transition state will be negative and the second derivative for a minimum point will be positive.
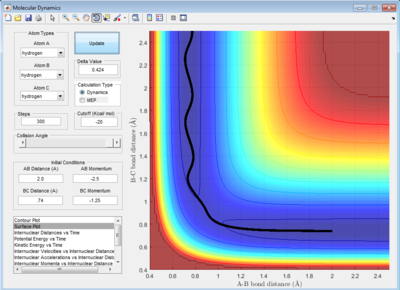
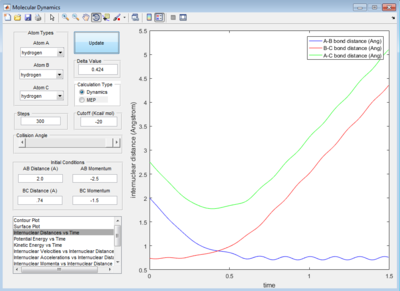
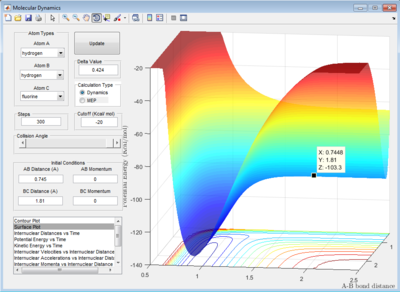
Trajectories from r1=r2: Locating the Transition State
The best estimate of the transition state position, rts is obtained by trial-and-error method with different initial conditions of r1 = r2 and p1 = p2 = 0 until it showed a least oscillation curve in internuclear distance vs time plot. The rts obtained is 0.908 Å. Because the internuclear distance vs time graph showed straight lines indicating that the molecule is almost not vibrating and atom is almost at stationary. The internuclear distance changes only by ± 0.0005 Å because the system undergoes a periodic symmetric vibration. The deviation is obtained from the fluctuation of the internuclear distances in the animation mode.
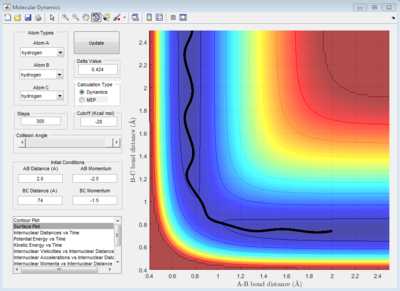
Trajectories from r1 = rts+δ, r2 = rts
The initial condition is set such that the system is slightly displaced from the transition state and zero initial momenta:
rBC = r1 = rts+0.01 = 0.918 Å
rAB = r2 = rts = 0.908 Å
p1 = p2 = 0
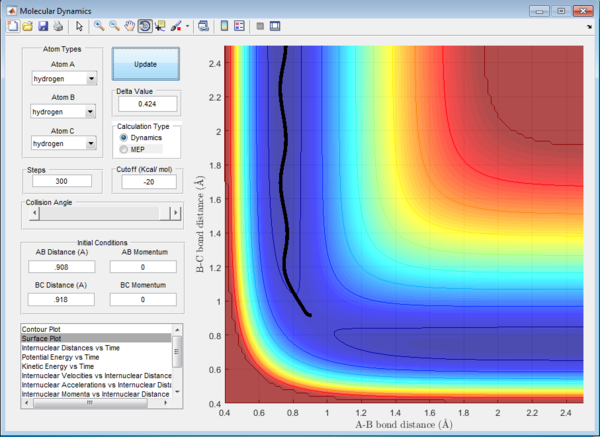
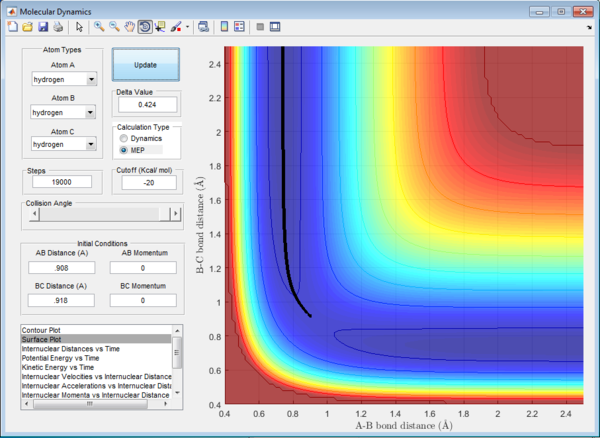
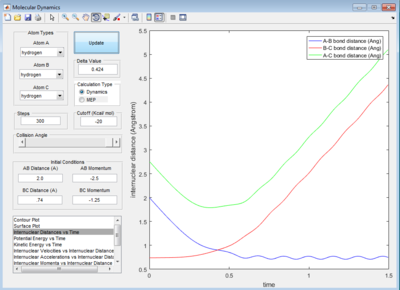
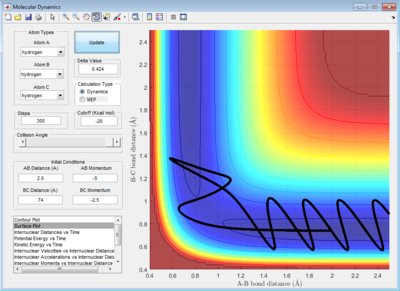
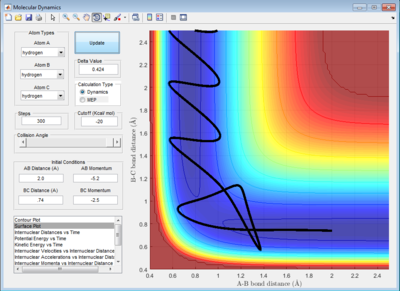
The trajectory in PES (potential energy surface) calculated by mep (minimum energy path) is rather smooth whereas the one calculated by dynamics is wavy and showing an oscillating behaviour. This is because mep is a very special trajectory that corresponds to infinitely slow motion (velocity is always reset to 0) and hence it doesn't provide a realistic picture of the motion of atoms during reaction. The oscillating behaviour in the product channel shows that the bond between HA and HB has formed and it is vibrating in the trajectory calculated by Dynamics.
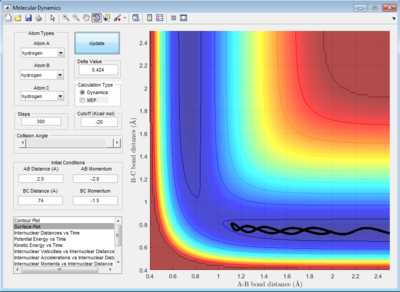
Reactive and Unreactive Trajectory
For initial positions of r1 = 0.74 Å and r2 = 2.0 Å, different momenta combinations had run to determine the reactivity of trajectories.
| Combination | p1/ Ns | p2/ Ns | Diagram | Reactivity | Description |
|---|---|---|---|---|---|
| a | -1.25 | -2.5 |   |
Reactive | As shown in the surface plot, rAB decreased in the entrance channel, showing that they are coming closer to each other and bond between HA and HB started to form. HBHC is not vibrating as rBC is not oscillating in the initial trajectory. After passing the transition state, the trajectory shown involves vibration in rAB (molecule HAB has vibrational energy) and rBC increased in the exit channel as atom HC leaves. This reaction can occur because both reactants have kinetic energies equal to or greater than activation barrier to pass through the transition state and hence forming the product.
In the internuclear distance vs time plot, there is a crossing point in the lines corresponding to rAB and rBC. At this particular time, rAB = rBC, indicating the formation of transition structure in this reaction. |
| b | -1.5 | -2.0 |   |
Unreactive | As shown in the surface plot, rAB decreased in the entrance channel, showing that molecule HBC and atom HA approach each other and bond between them might start to form. But, they have insufficient kinetic energy to overcome activation barrier hence not reaching the transition structure. This is supported by the internuclear distance vs time plot in which there is no crossing point in the lines corresponding to rAB and rBC. Hence, transition state is not reached. |
| c | -1.5 | -2.5 |   |
Reactive | The explanation is essentially the same as momenta combination 1 above except that there is oscillation in the entrance channel for rBC. The molecule HAB now has higher kinetic energy to vibrate as they has higher initial momentum, p1 than momenta combination 1. |
| d | -2.5 | -5.0 |   |
Unreactive | The molecule and atom have sufficient kinetic energy to overcome activation barrier and form the transition structure. Also, they have enough energy to recrossed that barrier and returns to reactants as indicated in the trajectory above. This is supported by the internuclear distance vs time plot in which there are 2 crossing points. This indicates that at these 2 particular times, rAB = rBC, and the transition structure formed twice in this reaction. |
| e | -2.5 | -5.2 |   |
Reactive | The molecule and atom have sufficiently high energy (momentum) to overcome the activation barrier thrice and eventually resulting in the formation of products. This is supported by the internuclear distance vs time plot in which there are 3 crossing points. This indicates that at these 3 particular times, rAB = rBC, and the transition structure formed thrice in this reaction. This trajectory shows that in exit channel is highly oscillating because this reaction has the highest momenta among all other combinations. |
Transition State Theory
Assumptions
1) The reactants and activated complex are in quasi-equilibrium. [1]
2) The rates of reaction can be calculated by focusing on activated complex or transition state which lies along a particular 'reaction coordinate' or a saddle point. [1]
3) The population of chemical species in various energy states follow Boltzmann distribution.[2]
4) The motion of chemical species along the reaction coordinate obey classical mechanics. [2]
- However, this assumption fails for reactions involving low molecular weight species. Quantum-mechanical tunneling must be applied to account for their motions.
5) Any activated complex that crosses the activation barrier must go on to form products of reaction, i.e. no recrossing of the activation barrier. [2]
- This is not entirely true as there is possibility that some trajectory may cross the barrier more than once, as illustrated in momenta combinations (d) and (e). Also, there is trajectory that being reflected back to reactant side although it had crossed that barrier and formed the transition state. This is illustrated in momenta combination (c).
Reaction 2: F-H-F system
PES Inspection
Energetics of Reaction
The enthalpy of reaction, ΔH can be determined from bond strengths by using the formula below:
ΔH = (Energy required in bond breaking)-(Energy released during bond formation)
The literature H-H and H-F bond strengths [3] are 436 and 570 kJmol-1 respectively.
| System | Chemical Reaction | ΔH/ kmol-1 | Energetics |
|---|---|---|---|
| F + H2 | F + H2 -> HF + H | 436-570= -134 | Exothermic |
| HF + H | HF + H -> F + H2 | 570-436= 134 | Endothermic |
Approximate Position of Transition State
| System | Diagram | Distance/ Å |
|---|---|---|
| F + H2 |  |
H-H = 0.745; H-F = 1.81 |
| H+ HF |  |
H-H = 0.745; H-F = 1.81 |
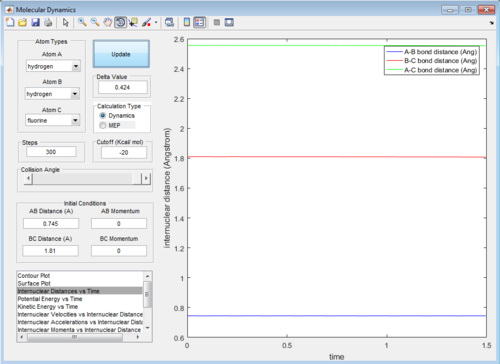
The approximate position of transitions were obtained by trial-and-error method, using different combination of distances with 0 momenta. By looking at the fluctuation of internuclear distance in animation mode, the H-H and H-F distances changed by 0.0002 and 0.002 Å respectively. Since the second system (H + HF) is just the reverse reaction of the first system (F + H2),hence the H-H and H-F bond distances are the same.
Activation Energy, Ea
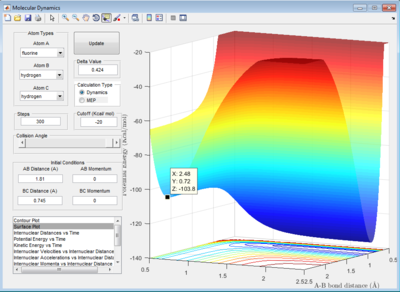
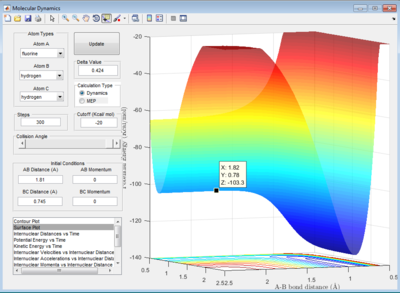
Activation energy is defined as the minimum kinetic energy that the reactants must have in order to form products. It is the potential energy difference between the reactants and transition state. The respective energies are determined from the surface plot as shown below.
| System | Diagram | Energy/ kcalmol-1 & Comment |
|---|---|---|
| F + H2 |   |
Reactant energy= -103.8
Transition state energy= 103.3 Ea= -103.3+ 103.8= 0.5 As shown in the surface plot, the products have lower energy than reactants, indicating that heat energy is released during the reaction. Hence, reaction between a F atom and H2 is an exothermic reaction. |
| H+ HF |   |
Reactant energy= -133.9
Transition state energy= -103.3 Ea= -103.3+ 133.9 = 30.6 As shown in the surface plot, the products have higher energy than reactants, indicating that heat energy is gained during the reaction. Hence, reaction between a H atom and HF molecule is an endothermic reaction. |
As seen from the surface plots above, The activation energy of H + HF system is greater than that of F + H2 system because H-F bond (570 kJmol-1) is stronger than H-H bond (436 kJmol-1). Hence, more heat energy is required to break the H-F bond.
Reaction Dynamics
Mechanism of Release of Reaction Energy
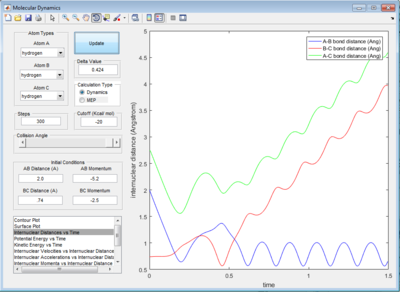
For the F + H2 system, the initial conditions are set as below:
rHH = 0.74 Å , rHF = 2.3 Å
pHF = -1.2 Ns , pHF = -1.3 Ns
The principle of conservation of energy [3] states that energy can neither be created nor destroyed. The total energy of an isolated system remains constant. So, it can only change from one form into another form.
As seen in the internuclear momenta vs time graph, it can be seen that the internuclear momenta between H initially oscillate with a small amplitude (vibration) then it became a straight line (translation). The internuclear momenta between H remains constant when the products had formed. On the other hand, the momentum between H and F started with a straight line and then it changed to an oscillatory graph with a much greater amplitude than momentum between H.
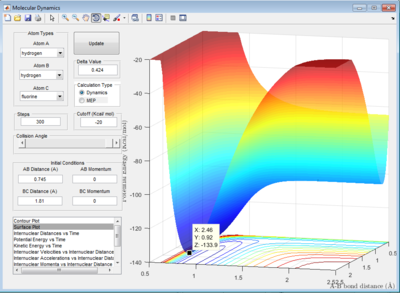
From the surface plot, the trajectory started off with a smaller amplitude and it changed to a much greater amplitude after passing the transition state. Both plot indicated that product HF had greater vibrational energy than reactant. Since the reaction is exothermic, the energy released during the reaction can be absorbed back by HF and stored as vibrational energy.
This can be confirmed experimentally by using infrared chemiluminescence [4] in which the weak infrared emissions product molecules formed in certain chemical reaction is measured and analysed. The energy released during the exothermic reaction is used to vibrationally excite the product, HF. This vibrationally excited product, HF decay to ground vibrational state by emitting a photon in the infrared region.
Also, by assuming the exothermic reaction is in the closed system, the increase in temperature can be measured using thermometer. The heat energy released can be calculated by: Q = mc∆T
where Q is the heat energy absorbed or released, c is specific heat capacity and ∆T is the change in temperature.
Polanyi's Empirical Rules [5][6]
The relationship between the distribution of energy between different modes (translation and vibration), the efficiency of the reaction, and the position of the transition state can be explained by Polanyi's rule. The Polanyi's rule describes how the transition state position affects the energy requirement and the energy disposal in an atom + diatom chemical system.
For an exothermic (early barrier) reaction, the reactant translational energy is more efficient than vibrational energy to overcome the barrier to form products. Hence, the reaction rate of an exothermic reaction with mainly reactant translational energy is higher than the one with mainly reactant vibrational energy. For an endothermic (late barrier) reaction, the reactant vibrational energy is more efficient than translational energy in promoting the formation of products. Hence, the reaction rate of an endothermic reaction with mainly reactant vibrational energy is higher than the one with mainly translational energy.
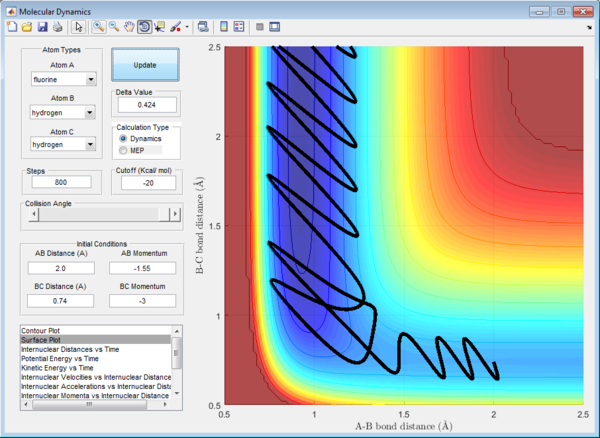
H2 + F -> HF + H Reaction
The initial conditions are set as:
rHH = 0.74 Å , rHF = 2.0 Å
pHH = -3 Ns , pHF = -1.55 Ns
For the exothermic H2 + F -> HF + H reaction, the trajectory shown in the surface plot has a wavy shape in the entrance channel. This indicates that reactants have more of vibrational energy arising from H-H stretch excitation than translational energy. This reaction is classified as inefficient although products formed in the end of reaction. This is because according to Polanyi's rule, for an exothermic reaction to be efficient, the reactants have to have more translational energy than vibrational energy.
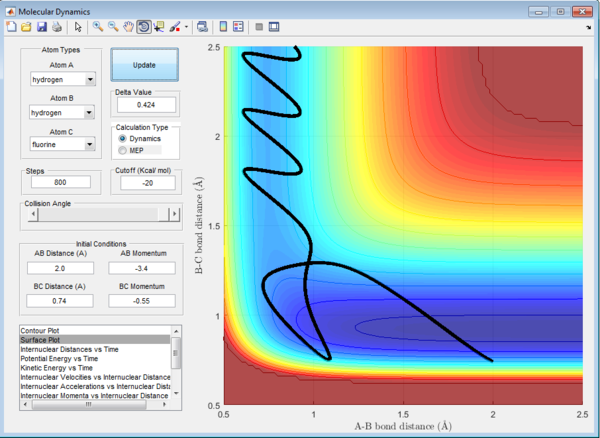
HF + H -> H2 + F Reaction
The initial conditions are set as:
rHF = 0.74 Å , rHH = 2.0 Å
pHF = -0.55 Ns , pHF = -3.4 Ns
For the endothermic HF + H -> H2 + F reaction, the trajectory shown in the entrance channel composed of mainly translational energy which is inefficient in promoting an endothermic reaction although products formed in the end of reaction.
References
- ↑ 1.0 1.1 Laidler, K.J. and King, M.C., 1983. Development of transition-state theory. The Journal of physical chemistry, 87(15), pp.2657-2664.
- ↑ 2.0 2.1 2.2 John W. Moore, Ralph G. Pearson, Kinetics and Mechanism, A Study of Homogenous Chemical Reactions, John Wiley & Sons, Inc, Canada, 1981
- ↑ 3.0 3.1 Richard Myers,The Basics of Chemistry, Greenwood Press, 1951 , 3, pp79. Cite error: Invalid
<ref>tag; name ":2" defined multiple times with different content - ↑ Polanyi, J. C., Infrared chemiluminescence, Journal of Quantitative Spectroscopy and Radiative Transfer, 3(4), 1963, pp 471-496
- ↑ Polanyi, J. C., 1972, Concepts in reaction dynamics, Accounts of Chemical Research, 5, pp. 161−168.
- ↑ Yan S., Wu Y., Liu K., 2008, Tracking the energy flow along the reaction path, PNAS, 105(35), pp. 12667-12672.