MRD:wjb115
Molecular Reaction Dynamics
Exercise 1:H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
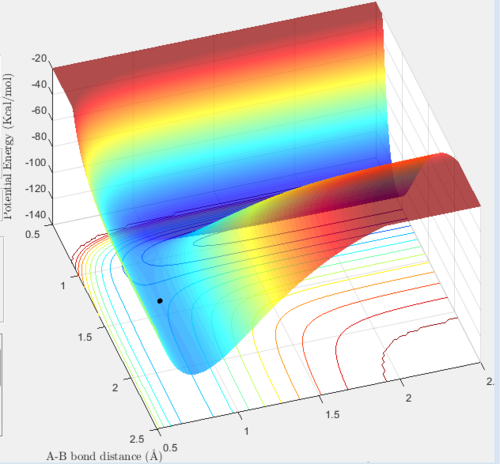
The total gradient of the potential energy surface, at a minimum, is zero, where ∂V(ri)/∂ri=0. At a transition structure ∂V(r1)/∂r1∂,V(r2)/∂r2=0, which means the potential energy is again 0. The transition state is found at the maximum on the minimum energy path, and as a result moving in one direction will give a maxima and the other direction a minima. Consequently, the transition structure can be considered a saddle point. Minima can be used to find the reactants, products and intermediates. In order to determine transition structures, start a trajectory near the transition state and observe whether it "rolls" towards the reactants or products.
The rolling analogy is not wrong but it's just that, an analogy. A more rigorous discussion is needed here, either discussing curvature with words or using second partial derivatives and their signs. Je714 (talk) 17:24, 31 May 2017 (BST)
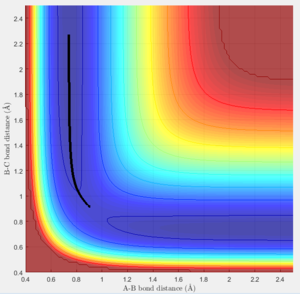
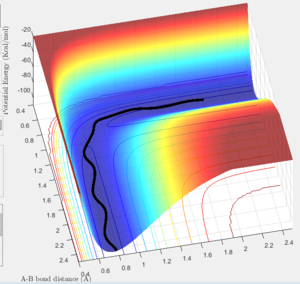
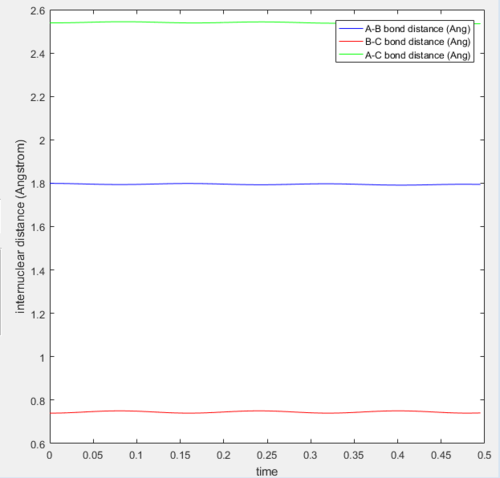
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
The transition state can be found on the maximum of the minimum energy path. By setting the momentum to zero and making r1=r2, it was possible to locate the transition state. Initially the bond lengths were set equal at just under 1.0Å, which was chosen using a plot of internuclear distance vs time. After trial and error with the distance, it was found that at 0.907Å the transition state is most likely to be found, since at this distance the trajectory oscillated and "never fell off". Never is a strong word. You can always run a sufficiently long trajectory and the TS geometry will be lost -- the TS is a mathematical construct which you can only get close to with arbitrary precision in practice. Je714 (talk) 17:24, 31 May 2017 (BST)
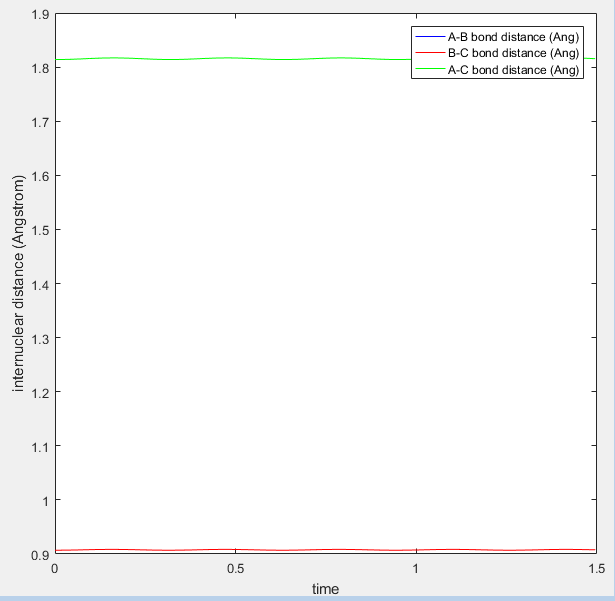
The above plot shows the internuclear distance vs time at a distance of 0.907Å, when the oscillations appeared to be at their lowest. Comment on how the mep and the trajectory you just calculated differ. r1=0.917 r2=0.907
Both the mep and dynamic calculated trajectories follow the minimum energy path in the valley, however, the plotted lines differ in each. In the mep the line is curved, but in dynamic it appears to be oscillating. This is a result of vibrational energy being neglected in the mep how is it neglected? That's what we're asking Je714 (talk) 17:24, 31 May 2017 (BST) , whilst in dynamic these changing vibrational energies are considered, and are responsible for the the wave-like oscillation of the dynamically calculated trajectory.
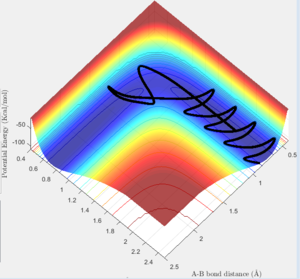
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
The initial positions used were r1 = 0.74 and r2 = 2.0, trajectories were then run with following momenta:
| Reaction Number | P1 | P2 | Reaction? |
|---|---|---|---|
| 1 | -1.25 | -2.5 | Yes |
| 2 | -1.5 | -2.0 | No |
| 3 | -1.5 | -2.5 | Yes |
| 4 | -2.5 | -5.0 | No |
| 5 | -2.5 | -5.2 | Yes |
This trajectory passes through the transition state and then proceeds to the products, making it a reactive process.
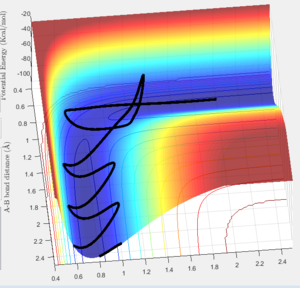
The trajectory is unreactive since when it reaches the transition state it "bounces" back towards the reactants instead of towards the products, as the energy barrier of the transition can not be overcome.
Again, the trajectory passes through the transition state and onto the products, making it a reactive process.
The trajectory shows barrier recrossing where the transition state is crossed twice, and the trajectory reverts back to the reactants. Consequently, this is an unreactive process.
Slightly different to the previous reaction, in this example the transition state appears to be crossed twice but instead of returning to the reactants there is sufficient energy to pass the activation energy of the reaction, so it can proceed towards products. This is therefore a reactive process.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The transition state theory is used to explain the reaction rates of elementary reactions. The theory assumes that the reactants and transition state structures, of a reaction, are in quasi-equilibrium which differs from classical chemical equilibrium. The theory is also based on the assumption that nuclei behave in classical mechanical sense, whereby a reaction can only proceed provided both the colliding molecules have sufficient energy to form the structure. This classical approach ignores the possibility of quantum tunneling, which states that reactions can occur even if the colliding molecules do not have the required energy to pass the energy barrier. At high temperatures the theory is also less useful as for some reactions it can fail. The theory is based on an idea that the reaction will pass through lowest energy saddle point on the potential energy surface, which at low temperatures is always true. However, as higher temperatures are reached molecules can populate vibrational modes. As a result of this, transition states may be far away from the lowest energy saddle point. Lastly, an assumption is made that every intermediate has a long enough lifetime for it reach a boltzmann distribution, before moving on to the next step of the reaction.
The quasi-equilibrium comment is not applicable in this case -- it's a statistical mechanic treatment of TST. We're looking at a triatomic collision in isollation -- we're not simulating an ensemble of particles. Otherwise good! Je714 (talk) 17:24, 31 May 2017 (BST)
Exercise 2: F-H-H system
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
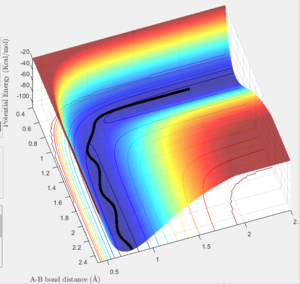
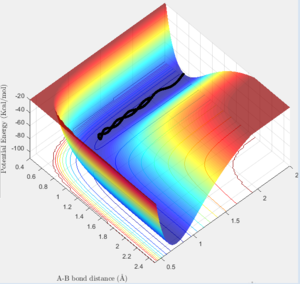
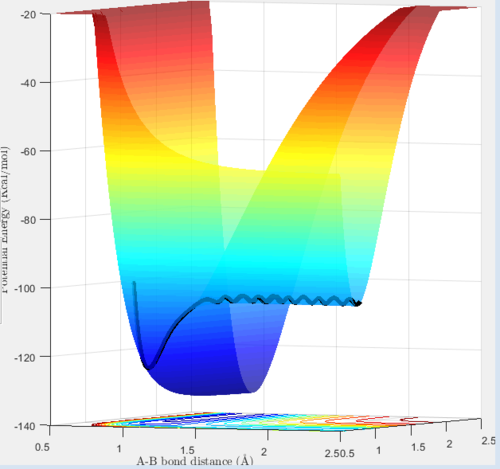
The reaction 'F + H2 ---> FH + H' has its trajectory shown below:
One can see from the graph that the potential energy of the products are below the potential energy of reactants. Consequently, this is an exothermic reaction as energy is being released. The converse can be said for the 'FH + H ---> H2' reaction, since it is simply the prior reaction in the reverse direction. Subsequently, the reactants would therefore site at lower potential energy than the products, so it would be considered an endothermic reaction.
This implies that the H2 molecule has a lower bond enthalpy than HF, since for a reaction to be exothermic 'bonds broken-bonds formed<0'. For this to be the case in 'F + H2 ---> FH + H' the bond dissociation energies of H2 must be lower than those of F-H, otherwise a negative value of bond enthalpy change could not be obtained.
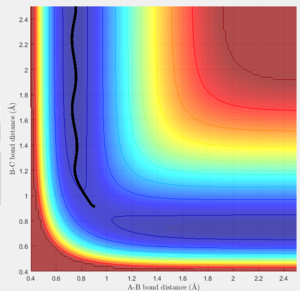
Locate the approximate position of the transition state.
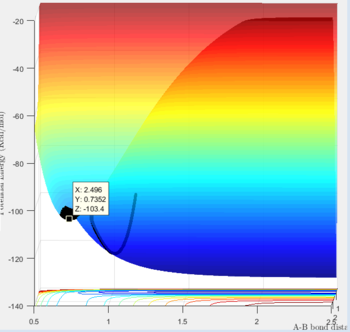
In order to determine the position of the transition state the same method as previously was used, where the momenta p1 and p2 were set to 0. The values of r1 and r2 were found using hammond's postulate. The reaction 'F + H2 ---> FH + H' has an early transition state which means it will resemble the reactants more than the products. With this in mind the transition state could be located using bond distances of r1=1.799 and r2=0.74. r1 was found more accurately using trial and error, after hammond's postulate aided in where to start to looking. Good Je714 (talk) 17:26, 31 May 2017 (BST)
The above graph shows bond distances at the transition state.
The above confirms a transition state as there is minimal oscillation.
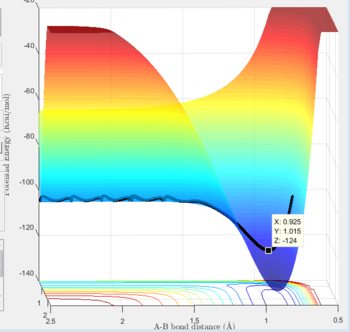
Report the activation energy for both reactions.
Activation energy is the difference between the energy of the reactants and the energy of the transition state.
'F + H2 ---> FH + H': The activation energy for this reaction was found to be (-103.3)-(-103.4)= 0.1 kJ/mol
'FH + H ---> H2': Activation energy = -103.3- -124= 20.7 kJ/mol
Values are a bit off. Je714 (talk) 17:26, 31 May 2017 (BST)
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
In any isolated system the total energy is always conserved. In this reaction potential energy is converted into kinetic and some vibrational energy. Initially, energy is stored as potential energy within the molecules, then as it proceeds towards the tranisiton state the potential energy is converted into kinetic energy. So as the potential energy decreases the kinetic energy increases. If, there is a successful reaction between the molecules, the energy is converted back to potential energy, as a transition structure is a potential energy maximum. Then as the reaction proceeds to make the products this potential energy is converted back into kinetic energy.
IR could be used to determine how much energy is converted into vibrational energy rather than kinetic. How? Give a bit more details. What vibration would you monitor? Any other experimental technique that you can think of? Think about temperature release... Je714 (talk) 17:26, 31 May 2017 (BST)
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The question of different modes of energy can be approached using Polyani's rules, in which he states that vibrational energy is more efficient in promoting a later transition state than kinetic energy. This would imply that in an exothermic reaction, where the transition state is early and resembles the reactants, having more kinetic than vibrational energy is preferable and would make this type of reaction more likely. The converse would be the case in an endothermic reaction, where the transition state is late, whereby vibrational energy would make this type of reaction more likely. The rules also states, however, that if the kinetic in an exothermic or vibrational in endothermic is too high then the reaction may proceed to the products, but then also reverse back to the reactants.
Missing some examples here Je714 (talk) 17:26, 31 May 2017 (BST)
References
1. Eyring, H. (1935). "The Activated Complex in Chemical Reactions". J. Chem. Phys. 3 (2): 107–115.
2. Atkins' Physical Chemistry. Atkins, P. and Paula, J. 10th edition. 2014.
3. Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction Zhaojun Zhang, Yong Zhou, Dong H. Zhang, Gábor Czakó, and Joel M. Bowman The Journal of Physical Chemistry Letters 2012 3 (23), 3416-3419
4.The reaction of F + H2→ HF + H. A case study in reaction dynamics, Faraday Discuss. Chem. Soc., 1977,62, 267-290, John C. Polanyi and Jerry L. Schreiber