MRD:wfbfmicou

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

At both a minimum and at a transition structure, the total gradient of the potential energy surface is zero. The points can be distinguished by their second derivative; the transition state is a saddle point. For a function $f (x, y)$ , at a stationary point $(a, b)$ consider the discriminant $D \equiv f_{x x} f_{y y} - f_{x y}^{2}$ :

If $D > 0$ , and $f_{x x} (a, b) > 0$ , the point (a,b) is a local minimum.

If $D > 0$ , and $f_{x x} (a, b) < 0$ , the point (a,b) is a local maximum.

If $D < 0$ , the point (a,b) is a saddle point.

If $D = 0$ , higher order tests are required.

I assume you've copied this over from wikipedia (https://www.wikiwand.com/en/Second_partial_derivative_test). It's not wrong, but: 1) Cite your sources 2) D is the determinant of the Hessian matrix Je714 (talk) 16:05, 31 May 2017 (BST)

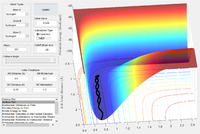
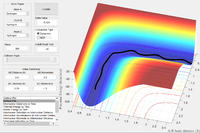
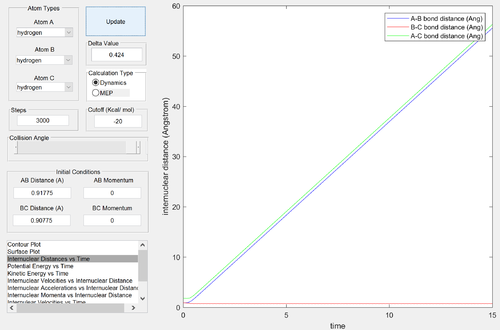
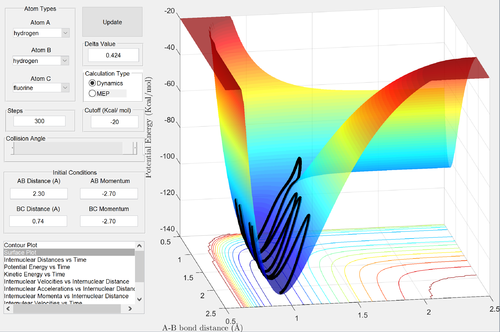
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

r_ts= 0.90775 Å

The internuclear distances remain effectively constant Why? Je714 (talk) 16:06, 31 May 2017 (BST)

this represents the metastable transition state.

Comment on how the mep and the dynamic trajectories differ.

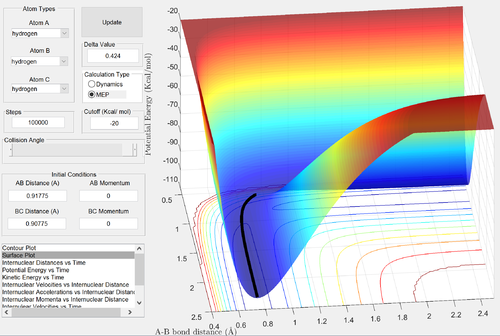
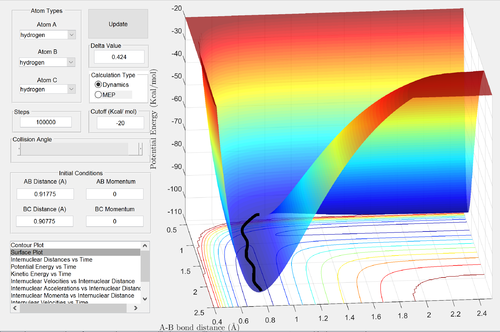
Good description Je714 (talk) 16:07, 31 May 2017 (BST)

In the MEP calculation, the kinetic energy of the particles is reset at each time step. The calculation begins at a structure similar to the transition state, with the H₁-H₂ distance slightly larger than the TS structure. As a result, the trajectory of the reaction in the MEP calculation follows the valley of the potential energy surface, without oscillating, to the reactants: H₁ and H₂-H₃. In the dynamic calculation, the inertia of the particles is taken into account: the velocities are not reset to zero at each step. Hence, vibrations are taken into account: the trajectory of the dynamic calculation also ends at the reactants, but oscillations are observed in this process.

How do internuclear distances and momenta vary with time, when a reaction coordinate on either side of the transition state is chosen?

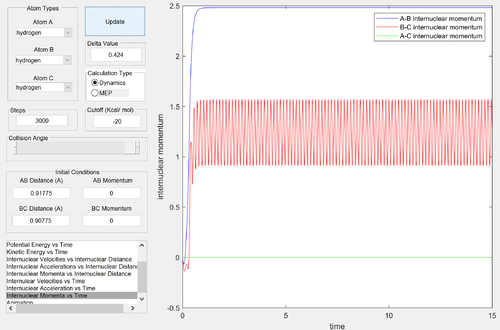
The transition state is symmetrical: changing the initial position from (r₁ = r_ts+δ, r₂ = r_ts) to (r₁ = r_ts, r₂ = r_ts+δ) simply results in the formation of H₁-H₂ + H₃ instead of H₁ + H₂-H₃. The internuclear momenta and distance-time relationships are identical, with labels swapped.

Reactive and unreactive trajectories

p₁	p₂	Outcome	Description
-1.25	-2.5	Reactive	The H₁-H₂ molecule initially has no vibrational energy: the initial kinetic energy is purely translational energy of the approaching H₃ atom. The H₃ atom has sufficient kinetic energy to lead to the formation of the transition state and the products are formed: this is a reactive trajectory. The resulting H₂-H₃ molecule is vibrationally excited.
-1.5	-2.0	Unreactive	The H₁-H₂ molecule is initially vibrating: this causes the oscillations in the A-B (H₃-H₂) distance. H₃ slows down as it approaches H₂, converting kinetic energy to potential energy. For this set of initial conditions, the kinetic energy of H₃ is insufficient to form the transition state and hence the products are not formed. H₃ is eventually expelled by the H₂-H₁ molecule: this trajectory is unreactive.
-1.5	-2.5	Reactive	This reactive trajectory is similar to the first case. The H₁-H₂ molecule is initially vibrating with small amplitudes. H₃ has sufficient kinetic energy to form the transition state and to expel H₁ from the molecule. Following the reaction, the H₃-H₂ molecule is vibrationally excited.
-2.5	-5.0	Unreactive	The H₂-H₁ molecule initially has no vibrational energy. The approaching H₃ atom has sufficient kinetic energy to reach the transition state: however, this particular set of initial conditions leads to barrier recrossing - the trajectory is unreactive. The large energies involved - far larger than required to reach the transition state - lead to a more unpredictable outcome. In this case, the transition state is so vibrationally excited that H₃ is ejected from the activated complex and the system returns to the reactants channel, with the H₂-H₁ molecule vibrationally excited as a result.
-2.5	-5.2	Reactive	This set of initial conditions is similar to the previous example, except in this case the barrier recrossing leads to the ejection of the H₁ atom from activated complex, giving the vibrationally excited H₂-H₃ molecule in the products channel.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for rate values compare with experimental values?

Transition State Theory (TST) is a model that simplifies the computational complexity of calculating trajectories along a potential energy surface. TST requires knowledge of the PES in the reactant and product channels, as well as at the transition state¹. A boundary is chosen - known as the critical dividing surface¹ - which intersects the saddle point of the potential energy surface. The main assumptions of TST of ideal gas reactions are:

- "All supermolecules that cross the critical dividing surface from the reactant side become products."¹

- "During the reaction, the Boltzmann distribution of energy is maintained for the reactant molecules."¹

- "The supermolecules crossing the critical surface from the reactant side have a Boltzmann distribution of energy corresponding to the temperature of the reacting system."¹

The 2nd and 3rd point are from a statistical point of view of TST. Not really applicable here, since you're only looking at a triatomic collision in isolation --- not at an ensemble of molecules Je714 (talk) 16:10, 31 May 2017 (BST)

As seen in the fourth example above, the assumption that all supermolecules with energy greater than the transition state lead to a reaction breaks down. In the fourth and fifth examples, barrier recrossing is observed in the trajectory calculations. Barrier recrossing is a phenomenon that is not accounted for in the transition state model. Therefore, transition state theory would predict larger rates of reaction than observed experimentally.

Good. This is the main point: it's what you're observing with your previous calculations. Je714 (talk) 16:10, 31 May 2017 (BST)

Neither TST nor the model used in this investigation account for a further complication - the effect of quantum tunnelling. For small particles that do not classically have the energy to overcome a potential barrier, there is a certain probability of quantum tunnelling through the barrier (which depends on the energy difference, tunnelling length, and mass). Therefore, in the example of H₃ + H₂-H₁, if the initial conditions lead to a collision which has insufficient energy to reach the transition state, tunnelling through the potential barrier to the other side of the PES and hence to the products is feasible. This phenomenon would lead to a small increase in the expected rate of reaction - however, the barrier recrossing effect dominates overall and hence we would still expect slower rates than calculated in TST.

What is a supermolecule? Good discussion of QM and acknowledging that it's not taking into account in these simulations Je714 (talk) 16:10, 31 May 2017 (BST)

Classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state. Report the activation energy for both reactions.

F + H₂

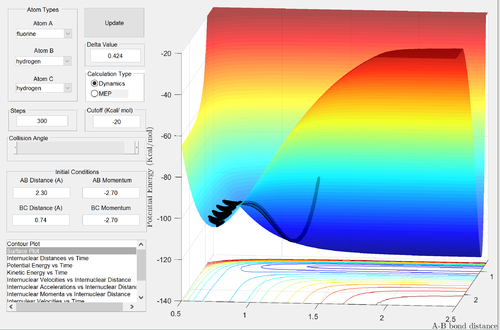
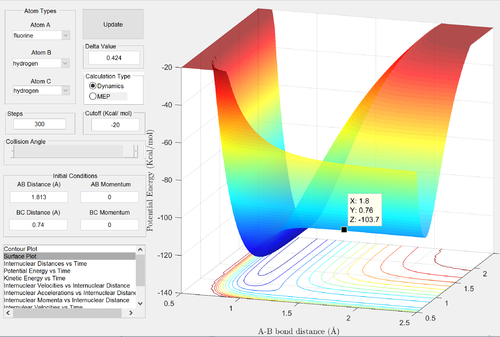
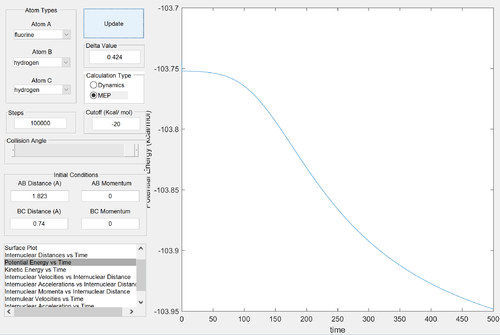
The reactants channel is higher in energy than the products channel: the reaction is clearly exothermic. Formation of a H-F bond releases more energy than the formation of a H-H bond: the H-F bond is stronger. Since the activation energy is small, the energies of the reactants and the transition states are similar: by Hammond's postulate, the transition state will resemble the structure of the reactants. Thus we expect the transition state to be located near the reactants channel: this can be seen above. Good reasoning Je714 (talk) 16:12, 31 May 2017 (BST)

To find the energy of the reactants, an MEP calculation was run from a structure nearing the transition state, with the F-H bond slightly stretched, to produce a potential energy vs. time graph. Similarly. the energy of the products was found from a structure nearing the transition state, with the F-H bond slightly compressed.

Energy of the reactants ≈ -103.95 kcal/mol

Energy of the transition state ≈ -103.75 kcal/mol

Energy of the products ≈ -133.85 kcal/mol

Activation energy ≈ 0.2 kcal/mol

Energy change of reaction ≈ -29.90 kcal/mol (negative because exothermic - release of energy)

Good discussion Je714 (talk) 16:12, 31 May 2017 (BST)

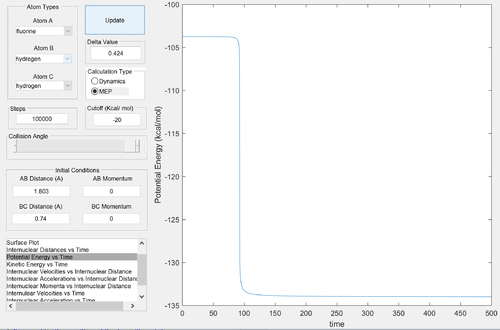
H + HF

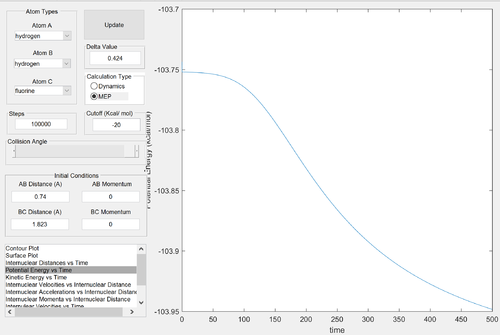
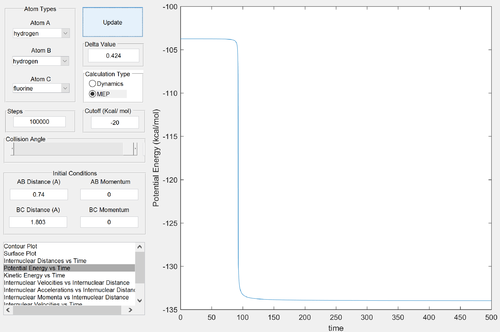
The reactants channel in the reverse reaction is lower in energy than the products channel: the reaction is endothermic. By Hammond's postulate, the transition state should resemble the structure of the products - the location of the transition state is very close to the products channel. Potential energy calculations against time were carried out for completeness - but since it is the reverse reaction of the above situation, it is clear that the energy calculations should be symmetrical.

Energy of the reactants ≈ -133.85 kcal/mol

Energy of the transition state ≈ -103.75 kcal/mol

Energy of the products ≈ -103.85 kcal/mol

Activation energy ≈ 30.0 kcal/mol

Energy change of reaction ≈ +29.90 kcal/mol (positive because endothermic)

F + H₂: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

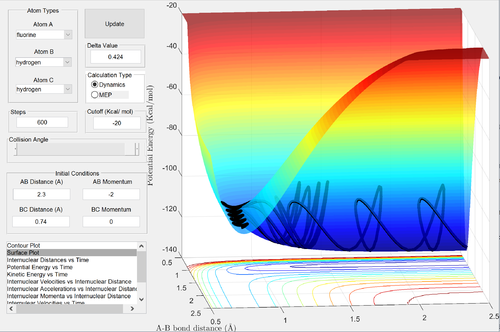
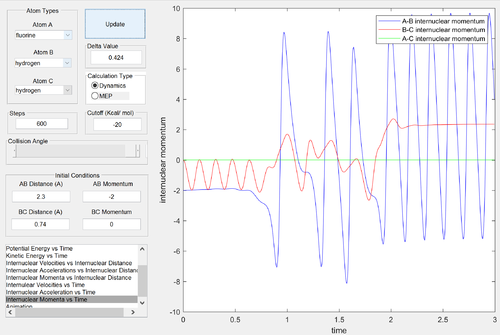
Following the reaction, the H-F molecule formed is vibrationally excited. This can be seen from the very large oscillations in the potential energy diagram and the internuclear momenta vs. time graph. The energy released in the reaction has been converted into vibrational kinetic energy - heat. The amount of heat energy dissipated by the reaction could be measured by calorimetry. The vibrational excitation of the H-F bond could be further confirmed by IR spectroscopy by comparing the IR spectrum obtained from the vibrationally excited products to the IR spectrum of a HF molecule at room temperature. At ambient temperatures, only the ground vibrational state is substantially occupied, as the vibrational temperature of the H-F bond is very large. Therefore, the transitions observed in the infrared spectrum of HF would be from the v = 0 to v = 1 state (and perhaps some v = 1 to v = 2 transitions). The lower vibrational levels closely follow the simple harmonic oscillator model, therefore the transitions occurring at room temperature would all involve the same energy and only a single line would be observed in the spectrum. The simple harmonic oscillator model breaks down at high vibrational levels for diatomic molecules. The energy spacings become progressively smaller until they converge at the dissociation limit, where the bond breaks due to the large vibrational energy. The HF molecule produced in this reaction is vibrationally excited, and its infrared spectrum would involve energy transitions that would match energy spacings in the anharmonic oscillator model. Therefore, in comparing its spectrum to room temperature, there would be a shift to many lower frequency absorptions, that would eventually converge to the dissociation limit (although the convergence point may not be experimentally observed, as the vibrational energy would most likely be dissipated to the environment such that the bond formed in the reaction wouldn't break).

Good discussion! Je714 (talk) 16:13, 31 May 2017 (BST)

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Good job giving examples Je714 (talk) 16:14, 31 May 2017 (BST)

F + H₂

The Polanyi rules refer to how the distribution of kinetic energy in the transition state affects whether a trajectory is reactive or unreactive. A higher proportion of vibrational energy promotes reactions with a late transition state, whereas a higher proportion of translational energy promotes reactions with an early transition state².

p_FH	p_HH	Outcome
-0.5	-2.8	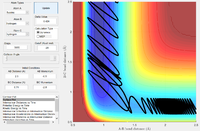Reactive
-0.5	-2.7	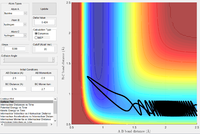Unreactive
-0.5	2.7	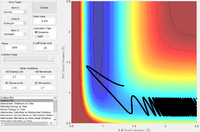Unreactive
-0.5	3.0	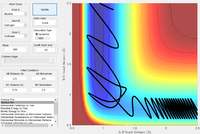Reactive
-0.8	0.1	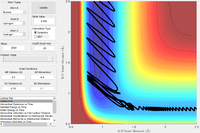Reactive

The F + H₂ reaction is exothermic, with a very early transition state, as shown above. Thus, according to the empirical Polanyi's rules, a higher proportion of translational energy would result in a reactive trajectory. This is clearly seen in the last example, where a significantly lower energy system results in a reactive trajectory: the kinetic energy is largely translational (there are only small oscillations in the reactants channel). In the first four cases, most of the kinetic energy in the system is in the form of bond vibrations. With p_HH = 3.0 and -3.0, the trajectory is reactive; small deviations in p_HH, however, result in unreactive trajectories. The system has a very large amount of energy compared to the activation energy, thus the outcomes of the trajectories become increasingly unpredictable.

H + HF

The H + HF reaction is endothermic, with a very late transition state, as shown above. Thus, according to the empirical Polanyi's rules, a higher proportion of vibrational energy would result in a reactive trajectory. Consider the following initial conditions:

p_FH	p_HH	Description	Outcome
-9.5	-10	High translational, low vibrational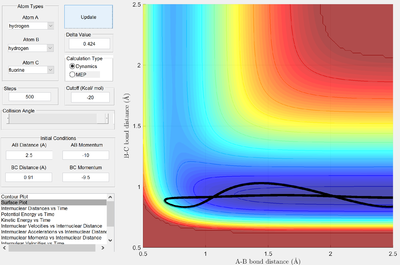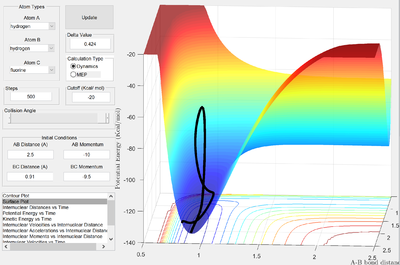
-10	-0.01	High vibrational, low translational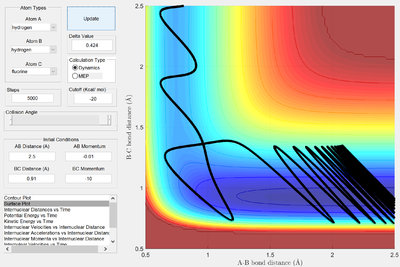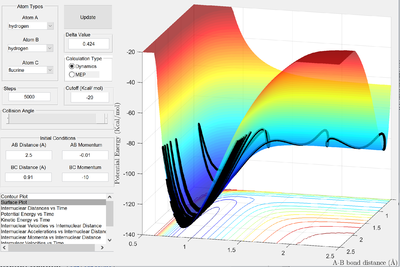

In the first case, where the H atom approaches the transition state with a high ratio of translational:vibrational kinetic energy, the trajectory is unreactive. It is clearly seen from the PES that the transition state will not be reached with purely translational motion: the transition state will just decay back to the reactants channel.

In the second example, there is a high ratio of vibrational:translational kinetic energy resulting in a reactive trajectory. The high vibrational energy result in the bond being closer to breaking, and hence the transition state is both easier to form and more likely to result in the formation of products. This is a demonstration of Polanyi's rules in action - but not a proof. The rules are only empirical and often fail to predict how systems behave².

References

1 I. N. Levine, Physical Chemistry, McGraw-Hill, Boston, Mass., 6th edn, 2009, pp. 893

2 Z. Zhang, Y. Zhou, D. H. Zhang, G. Czakó and J. M. Bowman, J. Phys. Chem. Lett., 2012, 3, 3416–3419.