MRD:vm371701349586

EXERCISE 1: H + H₂ system

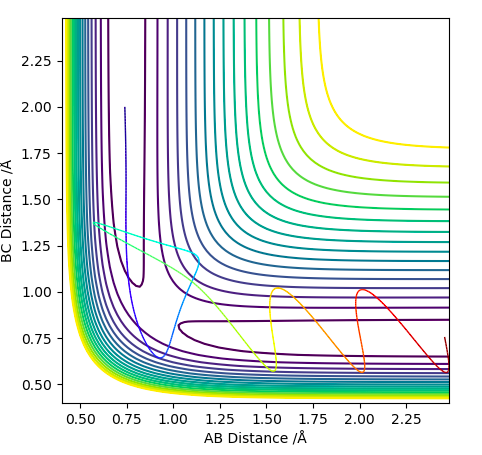
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

It is the maximum on the path representing the minimum energy for both the reactants and the products where the two lines cross. At the transition state, a slight change in geometry towards the reactants or the products will make the reaction favour the reactants or the products pathway.

This is definitely correct however the question is asking you to think about this more mathematically. It is at the minimum of the trough that is the trajectory of the reaction coordinate and therefore what does this mean about the partial derivative and also the second partial derivative of the curve at the transition state? And what of the partial derivative and second partial derivative for the direction in which it is the maximum? Rk2918 (talk) 21:15, 15 May 2019 (BST)

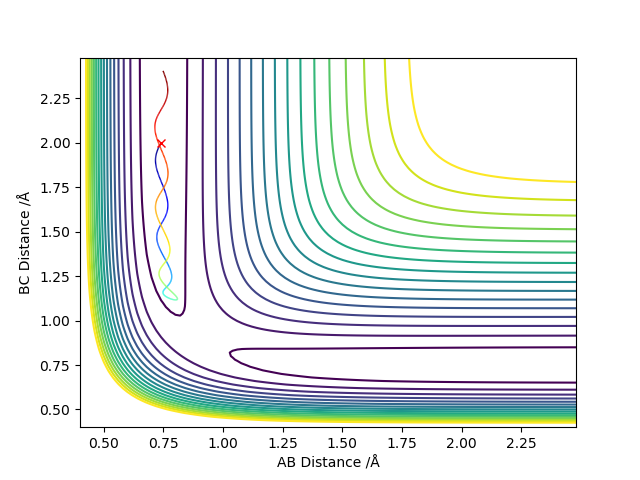
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

When the AB and the BC distances were set to 0.9 Å the atoms in the transition state vibrated the least and all the energy at all times was potential energy. On the "Internuclear Distances vs Time" plot we can see that the amplitude of oscillations is minimal compared to other values of AB distance.

Can you think any deeper about why that might be? What is the meaning of this lessened oscillation? Rk2918 (talk) 21:15, 15 May 2019 (BST)

Comment on how the mep and the trajectory you just calculated differ.

The mep does not account for the fact that after the collision the momentum of a single atom will be greater, because a single atom does not waste energy to vibrate while it travels in a translational mode.

There is more to the difference between mep and dynamics calculations which can be observed directly from the potential energy surface Rk2918 (talk) 21:17, 15 May 2019 (BST)

p1	p2	Etot	Reactive	Description of the Dynamics
-1.25	-2.5	-99	Yes	Fast approach of the atom, after collision the molecule slows down and the atom speeds up.
-1.5	-2	-100.5	No	The atom approaches the molecule slower, but the molecule is vibrating faster.
-1.5	-2.5	-98.95	Yes	The atom approaches the molecule faster, the molecule vibrates at a slower rate.
-2.5	-5	-84.9	No	The atom collides with the molecule very quickly, an H atom from H2 bounces twice on a single H atom, after that it collides back with the initial H it was bonded to and stays there.
-2.5	-5.2	-83.4	Yes	An H atom from H2 collides with the single H atom, bounces back to the initial H it was bonded to and thus bounces back on to the single H atom finally staying there.

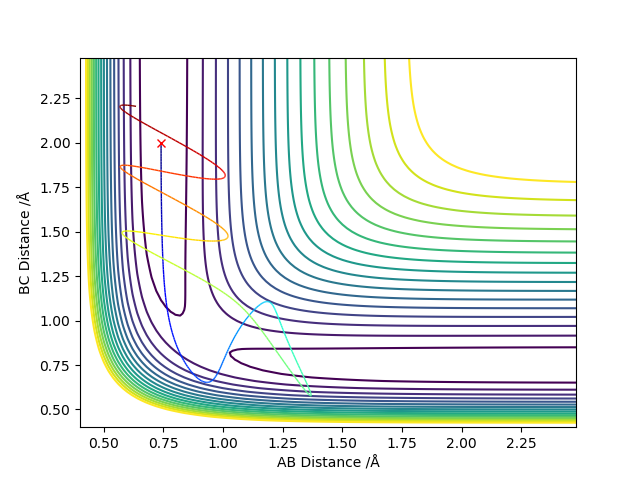
*In all cases, as the molecule and the atom approach each other both slowdown.

From the table above, it can be seen that small changes in the momentum of the atom approaching the molecule could affect whether the reaction occurs.

p1=-1.5, p2=-2

p1=-1.5, p2=-2.5

p1=-1.25, p2=-2.5

p1=-2.5, p2=-5

p1=-2.5, p2=-5.2

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The Quasi-Equilibrium assumption states that the reactants are only in equilibrium with the activated complexes that are about to move into the direction of products at the transition state. The results obtained in the simulations carried out show that even after the collision between one of the moelcule's atoms and the atom occurs, the atom from the molecule can still bounce back off to the original molecule it came from. Therefore, the experimental reaction rate values will be lower, since the activated complex on the graph of potential energy against reaction coordinate can still move into the direction of reactants.

EXERCISE 2: F - H - H system

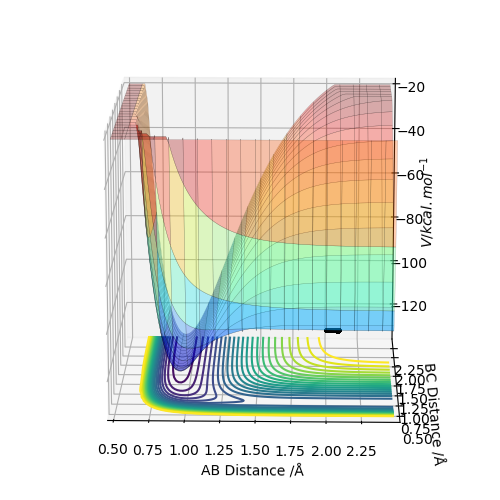
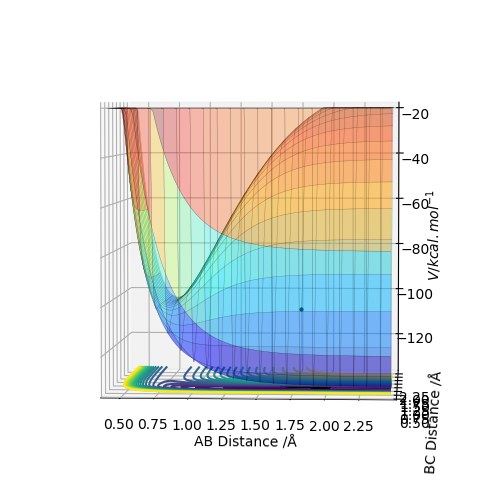
By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

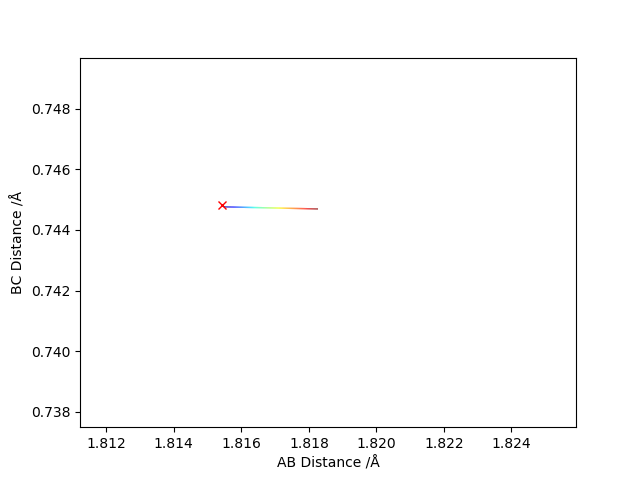
Locate the approximate position of the transition state.

As F approaches H2, the potential energy decreases, meaning that the reaction is exothermic. Thus, the H-F bond must be stronger than the H-H bond. Following from that, the backwards reaction must be endothermic.

This position is approximated as the Transition state, as we move slightly from the initial position the energy level changes only slightly.

As H approaches HF the potential energy increases, thus this reaction is endothermic and the H-H bond is weaker than the HF bond

Activation Energies:

Activation energy for the HF+ H reaction = +30.4 kcal/mol

Activation energy for the H + HF reaction = +0.125 kcal/mol

How did you calculate these activation energies? You need to provide a bit more explanation of how you have used the calculation procedures in order to demonstrate your understanding of them.Rk2918 (talk) 21:21, 15 May 2019 (BST)

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

As the molecule and the atom approach each other they both have potential energy and kinetic energy. In this case, the kinetic energy consists from translational and vibrational energies. After the reaction is complete, the potential energy is converted into kinetic energy of the molecule and the atom. Thus the overall energy is conserved.

This could be seen, if we slightly increase the momentum of the molecule H-H, the vibrational energy of the product molecule increases. Thus, potential energy was converted into kinetic energy.

An experiment to confirm this conservation of energy could be calorimetry.

You need to go into a bit of detail about what calorimetry is and how exactly it can be used to confirm conservation of energy.Rk2918 (talk) 21:21, 15 May 2019 (BST)

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

An exothermic reaction has an early transition state and requires a high translational energy approach, thus the momentum of the atom should be sufficiently high for the chemical reaction to occur. The endothermic reaction has a late transitional state and the reaction is favoured by a high vibrational energy in the molecule. Therefore, different transition states require a different distribution of kinetic energy for the reaction to occur.