Molecular Reaction Dynamics - Samuel Richardson

Exercise 1: H + H₂ system

What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

At a minimum and at a transition state structure, the total gradient of the potential energy surface is 0. These can be distinguished through obtention of second derivatives, as minimum points will give a second derivative which is greater than 0, and a transition state, since it is defined as the maximum of the minimum energy pathway, will have a second derivative which is less than 0.

(Remember, for each direction along the PES or coordinate, there is a derivative and a second derivative. You are implying there is only one coordinate to move along Tam10 (talk) 10:05, 17 May 2017 (BST))

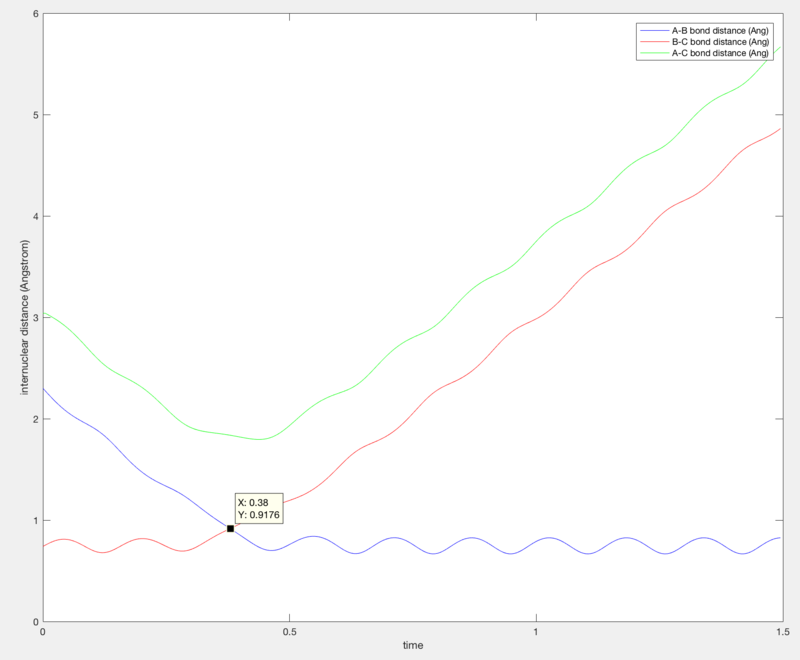
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.

r_ts ≈ 0.9176 Å

(This is only one condition for the TS. Refer back to what you said earlier about the gradient at the TS Tam10 (talk) 10:05, 17 May 2017 (BST))

Since the transition state is going to be symmetric, as all 3 atoms are identical, the transition state can therefore be identified as the point at which r₁ = r₂.

Comment on how the mep and the trajectory you just calculated differ.

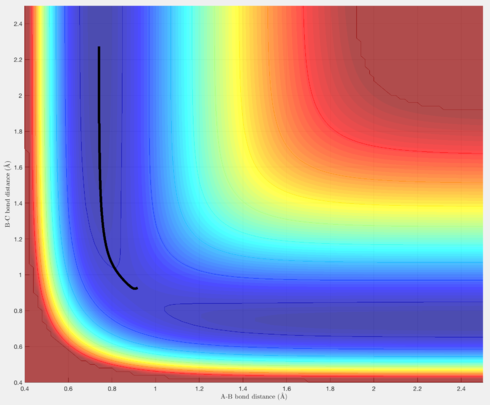
Under the Dynamics setting, vibrational motion is taken into account, and thus the trajectory oscillates, whereas under the MEP setting the trajectory simply travels along the floor of the valley corresponding to reactants.

Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.

p₁	p₂	Reactive/Unreactive?
-1.25	-2.5	Reactive
-1.5	-2.0	Unreactive
-1.5	-2.5	Reactive
-2.5	-5.0	Unreactive
-2.5	-5.2	Reactive

Figure 4: Screenshot of trajectory for p₁ = -1.25; p₂ = -2.5

Figure 5: Screenshot of trajectory for p₁ = -1.5; p₂ = -2.0

Figure 6: Screenshot of trajectory for p₁ = -1.5; p₂ = -2.5

Figure 7: Screenshot of trajectory for p₁ = -2.5; p₂ = -5.0

Figure 8: Screenshot of trajectory for p₁ = -2.5; p₂ = -5.2

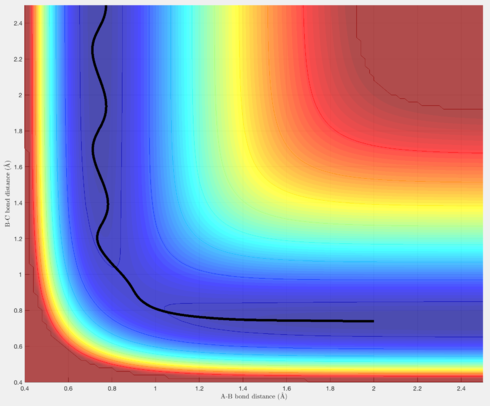
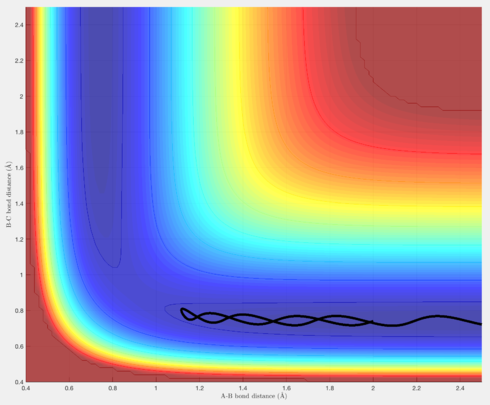
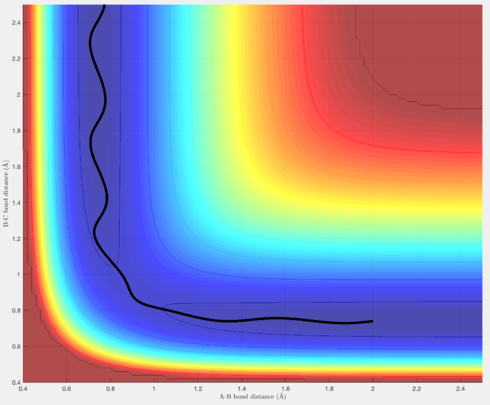
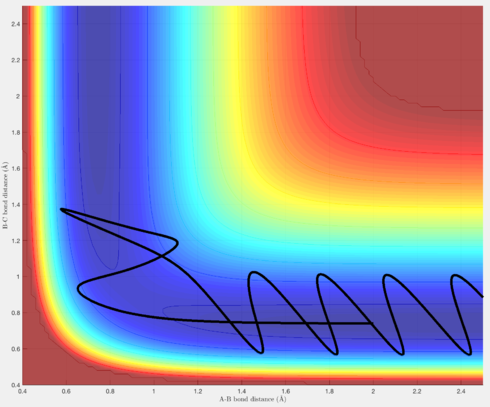
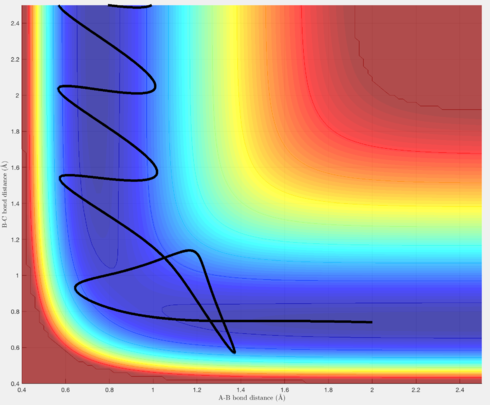
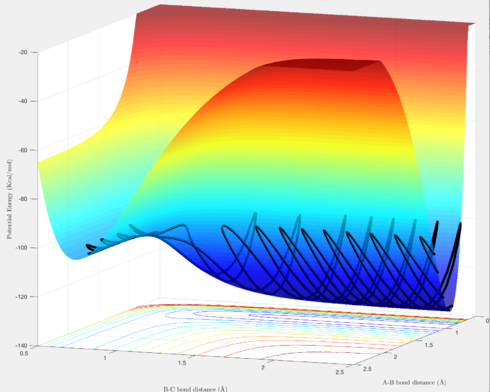
In terms of the trajectories, Figures 4 & 6 show reactive trajectories whereby the H atom approaches the H-H molecule, and each reactant possesses the right amount of momentum such that the trajectory proceeds over the transition state, then rolls into the products, where the newly formed H-H molecules vibrates, and the new H atom gets further away. Figure 5 shows a trajectory where the H atom approaches, but its momentum is not sufficient for it to "roll" over the transition state, and thus it rolls back into the reactants, and the process is unreactive. Figures 7 & 8 show trajectories whereby there is so much momentum, the barrier over the transition state is crossed to reach the reactants, but then, in the case of Figure 7, the leaving H atom has sufficient momentum to reverse its direction, and re-form the original H-H molecule, thus resulting in an unreactive trajectory. Figure 8 is similar, except after the trajectory rolls back into the reactants, there is still sufficient momentum for the trajectory to pass over the transition state again and roll into the products, resulting in a reactive trajectory.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition State Theory (TST) assumes that a) all supermolecules that cross the critical surface become products, if they have come from the reactant side, and reactants, if they have come from the product side, b) the products possess the same Boltzmann energy distribution as the reactants, and c) any supermolecules crossing the critical surface have a Boltzmann energy distribution corresponding to the temperature of the system^[1]. Since TST does not account for quantum mechanics, or, in the case of light species, tunneling, the computed reaction rates are likely to be significantly lower than experimental values.

Exercise 2: F - H - H system

Classify the F + H₂? and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

F + H₂ = Exothermic; H + HF = Endothermic

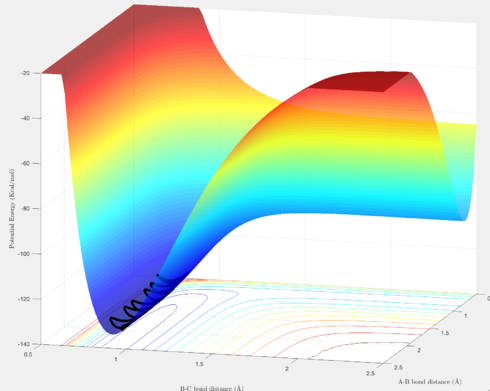
Figures 9 & 10 clearly show a decrease and increase in energy, respectively, from reactants to products, corresponding, respectively, to an exothermic and endothermic reaction. This makes sense, since the H-F bond is significantly stronger than the H-H bond (565 kJ/mol vs 436 kJ/mol, respectively^[2]), and thus is enthalpically favourable.

Locate the approximate position of the transition state

H-H ≈ 0.75 Å; H-F ≈ 1.81 Å

Report the activation energy for both reactions.

E_a for F + H₂ = +0.25 kcal/mol

E_a for H + HF = +30.3 kcal/mol

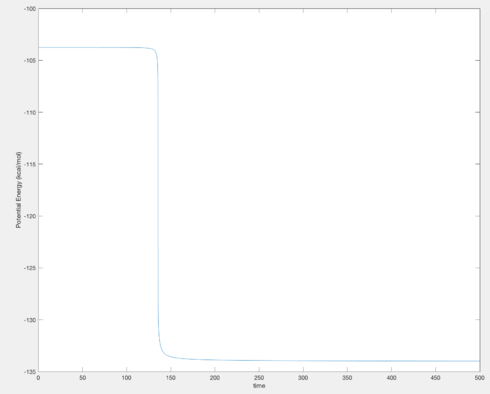
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

Figure 14: Internuclear Momentum vs Time graph for F + H₂ (*r₁ = 0.74; r₂ = 2.3; p₁ = 0; p₂ = -2.7*)

It can be seen from Figure 14 that from the reactants to the products, there is a significant increase in vibrational energy, which is clearly the way in which the increased translational potential energy in the reactants in conserved in this reaction. This could be confirmed by IR spectroscopy, which would show a much higher wavenumber for the product's vibrations than those of the reactants.

(This would only confirm the presence of a new bond. It wouldn't show how the energy is released Tam10 (talk) 10:05, 17 May 2017 (BST))

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's Empirical Rules state that for a late transition state, vibrational energy is more efficient than translational energy in producing a reactive trajectory, and vice versa for an early transition state^[3].

Figure 15: Unreactive trajectory for F + H₂ (*r₁ = 0.74; r₂ = 2.3; p₁ = -2; p₂ = -0.5*)

Figure 16: Reactive trajectory for F + H₂ (*r₁ = 0.74; r₂ = 2.3; p₁ = 0.1; p₂ = -0.8*)

Figure 17: Unreactive trajectory for H + HF (*r₁ = 0.92; r₂ = 2.3; p₁ = 5.4; p₂ = -5*)

Figure 18: Reactive trajectory for H + HF (*r₁ = 0.92; r₂ = 2.3; p₁ = 5.5; p₂ = -3*)

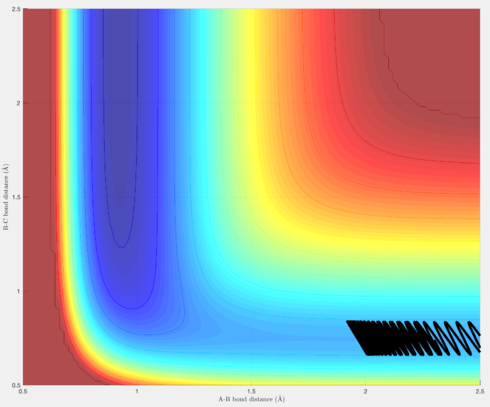
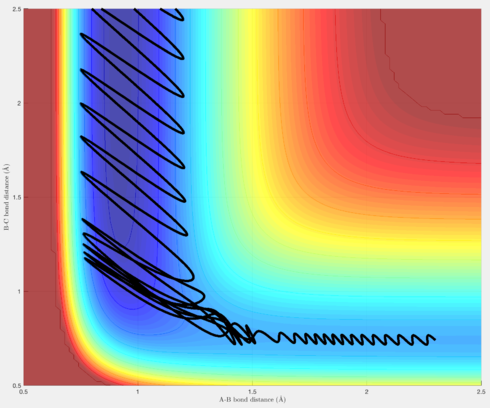
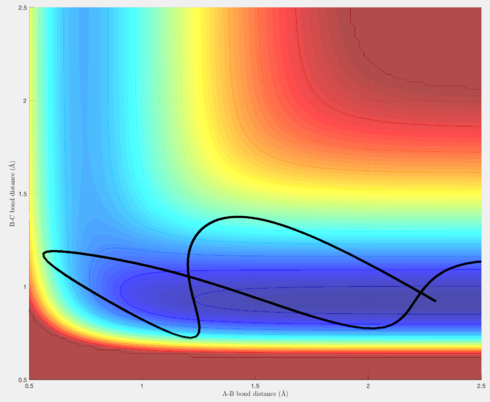
Figures 15-18 are a demonstration of this. Figures 15 & 16 are trajectories for the reaction F + H₂ -> H + HF, and as seen earlier, possesses a transition state closer to the reactants than the products (an early transition state). Polanyi's empirical rules therefore state that translational energy will be more efficient in producing a reactive trajectory than vibrational energy, and as seen in figures 15 & 16, although the overall energy of the system decreases from figure 15 to figure 16, because there has been an increase in the translational energy, this is sufficient to produce a reactive trajectory.

Similarly, for the reaction H + HF -> H₂ + F, there is a late transition state, and this Polanyi's empirical rules state that vibrational energy should be more efficient in producing a reactive trajectory than translational energy. Figures 17 and 18 demonstrate this, as, again, although the overall energy of the system decreases from figure 17 to figure 18, because there is more vibrational energy present, this is enough to produce a reactive trajectory.

References

[1]: Levine IN. Physical chemistry. 6th Edition. Boston, [Mass.]: McGraw-Hill Higher Education; 2009;p.893

[2]: Atkins P, de Paula J. Physical Chemistry 8th Edition. Oxford: Oxford University Press;2006;p.1011

[3] Polanyi JC. Concepts in reaction dynamics. Acc Chem Res. 1972;5(5):161–8. Available from: http://dx.doi.org/10.1021/ar50053a001 [Accessed 11th May 2017]