MRD:sp3815
H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
At the minimum of the potential energy surface the total gradient is equal to zero. The transitions structure has a maximum potential energy compared to the reactants and products and therefore the transition structure is at the maxima of the potential energy curve and the gradient at the maximum is equal to zero.
(You've said that the gradient of both is 0. If this is the case then how can the curvature be used to distinguish a maximum, minimum and a transition state? Lt912 (talk) 22:48, 18 May 2017 (BST))
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
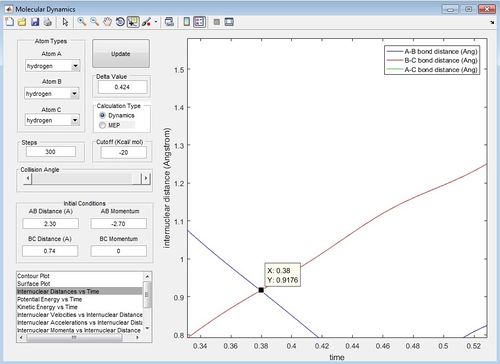
The internuclear distance at the transition state is determined by the point at which the A-B bond distance and B-C bond distance lines overlap and at this point the internuclear distance is 0.9176 Angstroms.
At the transition state position the AB and the BC distance are equal and therefore the AB and the BC distances were both set to 0.9176 A, this gave the following internuclear distance-time plot.
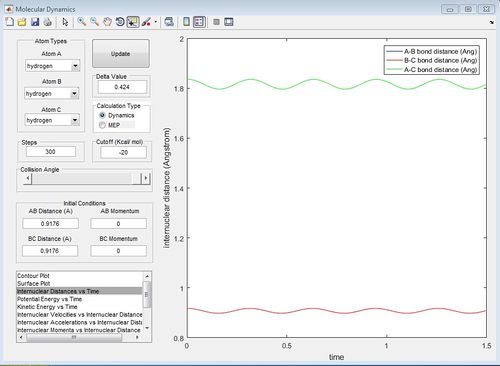
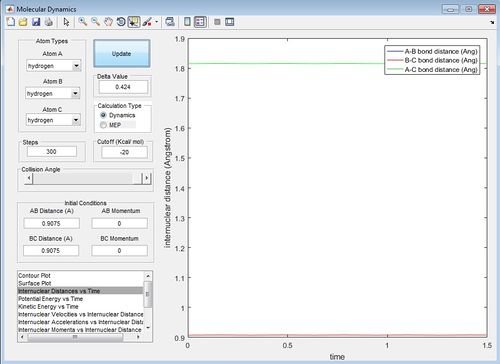
The AB and BC distances are then optimised around 0.9176 A to obtain the internuclear distance against time which gives the A-B bond distance and the B-C bond distance on the internuclear distance against plots as straight lines, this therefore shows that at this A-B (B-C) distance there is no oscillation of the transition state. The distance where the two lines are straight is at 0.9075 A.
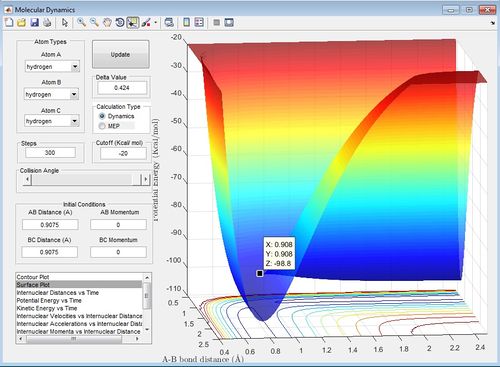
Comment on how the mep and the trajectory you just calculated differ.

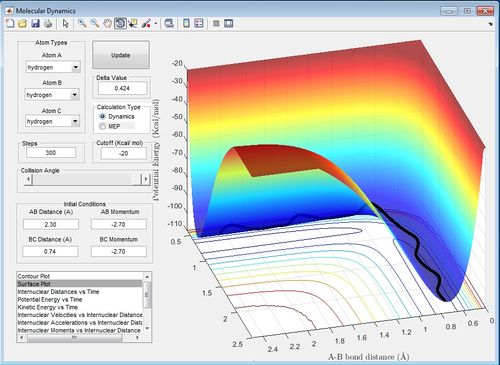
The mep is the minimum energy pathway and does not account for a real system. In the mep there is no vibrations of the molecules. However, the trajectory shows the whole reaction pathway and there is vibration of the initial reactant molecule and final product molecule. This trajectory approach is accounts more for a real system.
Initial positions correspond to the final positions of the trajectory, the same final momenta values but with their signs reversed. What do you observe?


Therefore for the original parameters r(AB)=0.7114 A, r(BC)=5.462 A, p(AB)=5.419 and p(BC)=2.983.
For the 0.9175 and the 0.9075 parameters, r(AB)=5.491 A, r(BC)=0.7209 A, p(AB)=3.561, p(BC)=0.3692.
Therefore when the original parameters are used then an AB bond forms and the BC bond breaks as the AB final internuclear distance is smaller than the BC final internuclear distance. However, when the parameters are changed to r1 = rts and r2 = rts+0.01 then the BC bond forms and the AB bond breaks as the AB final internuclear distance is smaller than the final BC internuclear distance.



Therefore with the original parameters the calculation with the final internuclear distances and minus the final momentum shows that the reverse reaction takes place. In this case the BC bond forms and the AB bond breaks. This is because the atoms have the same momentum as before but the momentum is applied in the opposite direction and therefore the molecules move in the reverse direction in the reaction pathway.
Reactive and unreactive trajectories
| p1 | p2 | Reactive or unreactive |
|---|---|---|
| -1.25 | -2.5 | reactive |
| -1.5 | -2.0 | unreactive |
| -1.5 | -2.5 | reactive |
| -2.5 | -5.0 | unreactive |
| -2.5 | -5.2 | reactive |
The reactive trajectories show path from the reactants to the products. Therefore the second example is unreactive because the trajectory loops onto itself without reaching the products. The penultimate example is unreactive due to barrier recrossing.


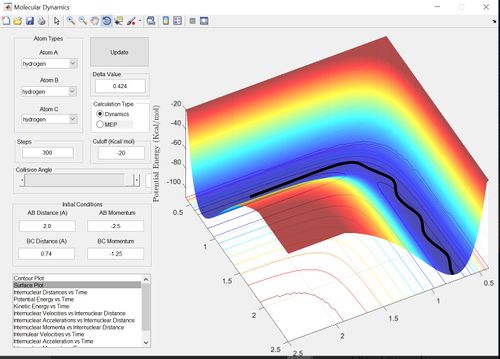
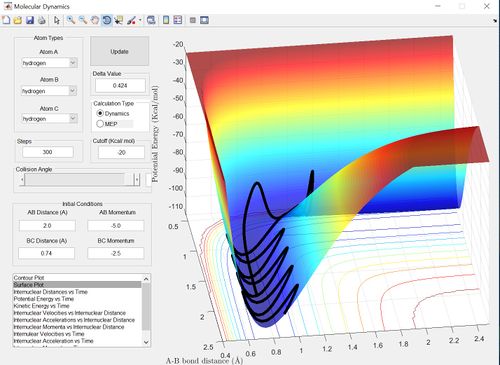
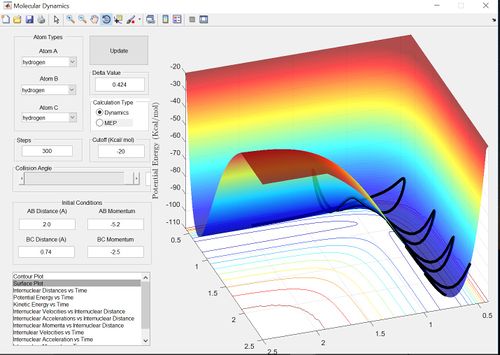
The main assumption of transition state theory is that the motion of the atoms or molecules follow classical mechanics. Transition state theory also assumes that unless the atoms or molecules collide with enough energy to form the transition state then the reaction does not occur. However, in the penultimate set of conditions (p1=-2.5 and p2=-5.0) there is barrier recrossing and therefore the reactants have enough energy to form the transition state and the product transiently, however, the system then reverts back to the reactants. Therefore transition state theory would predict a greater rate of reaction for this reaction then the actual experimental value.
F - H - H system
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 reaction is exothermic and the HF + H reaction is therefore endothermic. This correspond to the HF bond being stronger than the HH bond.
Locate the approximate position of the transition state.
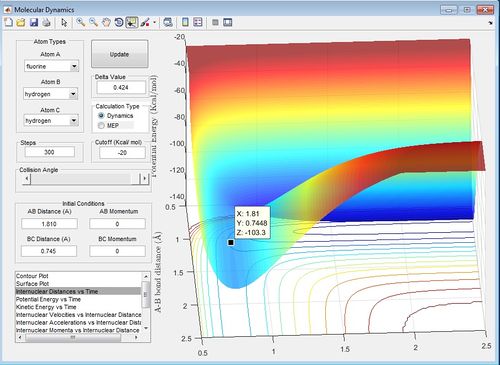
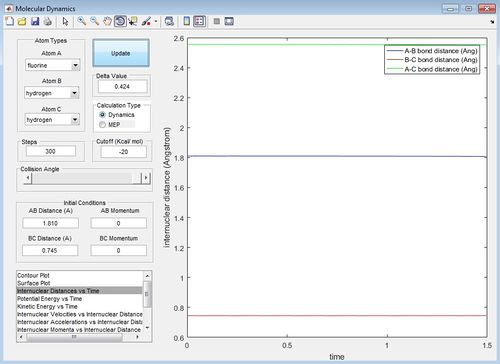
The internuclear distance against time graph for the H2+F reaction with the AB distance equal to 1.810 A and the BC distance equal to 0.745 A is the transition state position because the AB bond distance and the BC bond distance lines are straight on the internuclear distance against time graph and therefore none of the atoms or molecules involved in the reaction are vibrating.
Report the activation energy for both reactions.
The activation energy was calculated using the mep. The AB and BC distances were set to a small deviation from the transition state distances and the number of scans is increased.
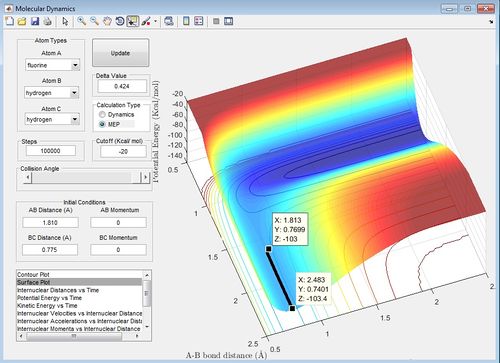

Therefore the activation energy of the H2+F reaction is 0.4 kcal/mol and the activation energy for the HF +H reaction is 30.1 kcal/mol. The H2 + F reaction is an exothermic reaction, the transition state is a closer energy to the reactants which is H2 and F, this is predicted by Hammond's Postulate.
Discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
In an exothermic reaction, the reactants have a higher potential energy than the products, however, the principle of conservation of energy states that energy cannot be created or destroyed. Therefore some of the potential energy of the reactants is converted into vibrational and transnational energy on going to the products. The ratio of the vibrational and translational energy determines whether the reaction proceeds. The product molecules therefore have a higher vibrational energy than the reactants. Therefore an IR spectroscopy is used to measure the vibrations of bonds in a molecule and therefore comparison of the reactant and product IR can be used to confirm the release of reaction energy experimentally.
(I think this would just show you've made a bond, not that it's vibrationally excited. Lt912 (talk) 22:59, 18 May 2017 (BST))
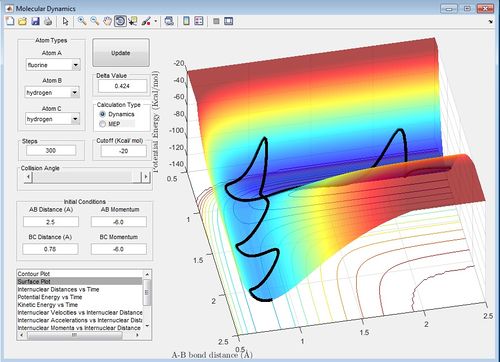
Reactive Trajectory for the H2 +F Reaction
The reactive trajectory has r(AB)=2.5 A and r(BC)=0.78 A, p(AB)=-6.0 and p(BC)=-6.0. In this trajectory the reactants are converted from reactants to products.
Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 0.74, with a momentum pFH = -0.5, and explore several values of pHH in the range -3 to 3 (explore values also close to these limits). What do you observe?
In this system where pFH=-0.5 and the pHH is varied between -3 and 3, there is insufficient energy to overcome the activation energy at the transition state to get the products. For all the pHH values in he -3-3 range, there is only vibrations of the reactant molecules present. However, the greater the magnitude of the momentum given to BC, the greater the vibration of the reactants. This is shown by comparison of the surface plots for pHH=3 and pHH=0 which shows greater vibration for pHH=3. This can also be shown by comparison of the internuclear momentum against time for pHH=-3 and pHH=0. The oscillation of the internuclear momentum against time for pHH=-3, the greater the maximum value for the internuclear momentum oscillation.
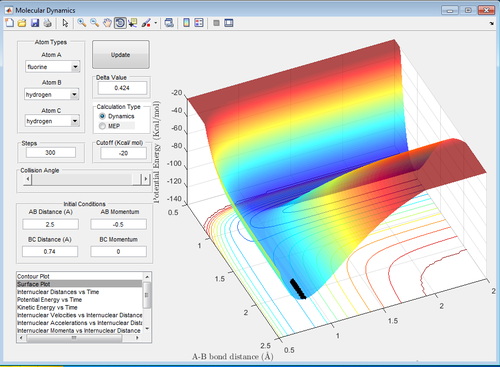
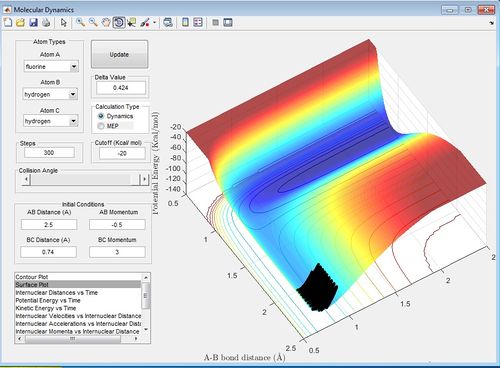
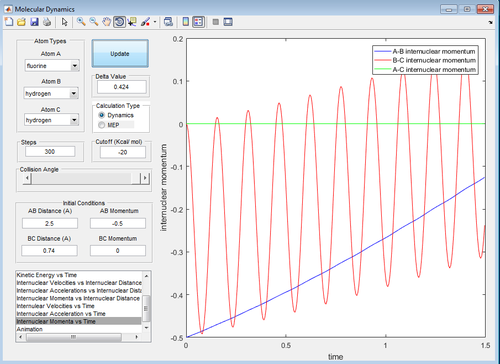
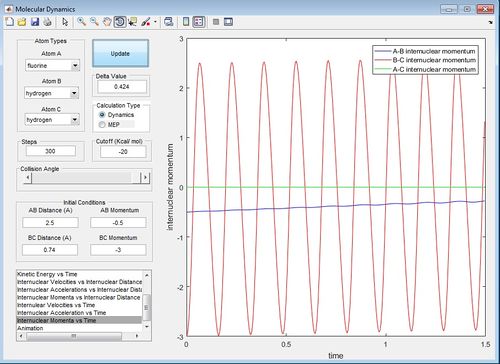
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The ratio of AB momentum to BC momentum which results in a reaction pathway from H2 to F to the products is -3 to -2 as shown in the surface plot below. This reaction is inefficient because because there is recrossing of the barrier. In this reaction, potential energy from the reactants is converted into vibrational and translational energy in the products and therefore in the surface plot shown below, the products have greater vibration than the reactants. Therefore the ratio of vibrational to translational energy is greater for the products than the reactants. The ratio of the vibrational and translational energy determines the position of the transition state (i.e. late or early).
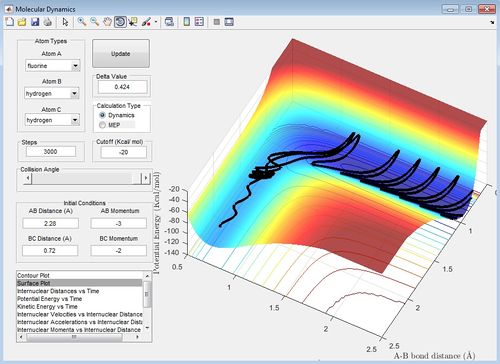
(The efficiency of a reaction does not relate to barrier recrossing. If you had a bunch of trajectories with high vibrational energy and low translational energy and a second bunch with low vibrational and high translational - which set would be better at delivering successful reactions? Lt912 (talk) 23:07, 18 May 2017 (BST))
The ratio of vibrational and translational energy does not determine the position of the transition state. If this was true the transition state would be different for each trajectory, even if the trajectories describe the same reaction. Lt912 (talk) 23:07, 18 May 2017 (BST))
