MRD:smw01079889rbsd
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The total potential energy gradient at both the minimum point and the transition state is zero. The two points could be distinguished from the sign of the value of its second derivative.
The minimum energy point would give a value for the second derivative which is greater than zero (Positive) because the minimum point involves a change in the sign of the gradient from negative (a decrease in potential energy) to positive (an increase in the potential energy of the system). This thereby generates an overall positive rate of change in the gradient which is quantified by the value of the second derivative.
At the transition structure, the point on the surface would a saddle point (minimax) where the second derivative would give a value of zero. Here the rate of change of gradient before the point is approached is opposite in sign to after passing the point. Therefore the overall rate of change in the gradient is zero. Just before the transition state is reached, the rate of change in potential energy per unit inter-nuclear distance is positive due to large repulsion and just after the separation of the transition state, the value is negative.
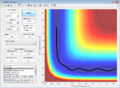
(Fv611 (talk) 14:23, 9 June 2017 (BST) good, but remember that being a saddle point, the TS is only a maxima in the direction of the reaction coordinate) Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
The best estimate for r(ts) = 0.9176 A. This was obtained from the inter-nuclear distance vs time plot and the point of intersection of rab and rbc curves.
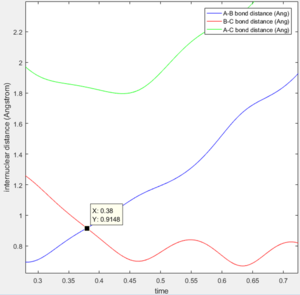
(Fv611 (talk) 14:23, 9 June 2017 (BST) The coordinates are correct, even though you don't explain what distance does r(ts) correspond to. However you are not explaining why the TS is the intersection of r(ab) and r(bc).) Comment on how the mep and the trajectory you just calculated differ.
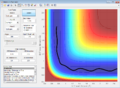
The mep gives a smooth curve with a straight line whereas dynamic contains sinusoidal fluctuations.
In mep velocity is set to zero such that it will accelerate to minimize its potential energy.
In dynamic, at each step the atom will have an initial velocity which is coupled to the acceleration and it causes oscillations at each step.
(Fv611 (talk) 14:23, 9 June 2017 (BST) Not really. Acceleration is equal to velocity over time so setting the velocity to zero will not accelerate anything. And even if the system did have higher velocity as the time progresses, why would that impact potential energy?)
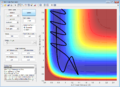
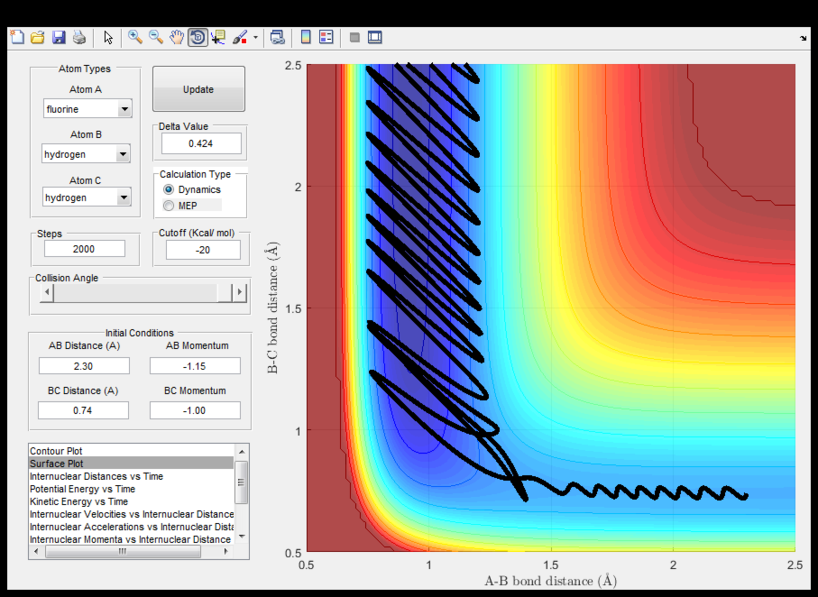
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| p1 | p2 | Trajectory | Reactivity | Description |
|---|---|---|---|---|
| -1.25 | -2.5 | Reacts | The atoms have sufficient energy to reach the Transition state and the bond oscillates due to vibrations. | |
| -1.5 | -2.0 | Doesn't react | The atoms even though approach each other, do not have enough energy to react. | |
| -1.5 | -2.5 | Reacts | The same principle as the first one but here the initial trajectory of A-B vibrates due to higher p1 momentum
and therefore high kinetic energy to react. | |
| -2.5 | -5.0 | Reacts and return to initial state | The products return back to initial trajectory and reform the reactants. | |
| -2.5 | -5.2 | Reacts twice | The trajectory cross the transition state twice. |
(Fv611 (talk) 14:23, 9 June 2017 (BST) Correctly identified the reactive trajectories. However, could have added more discussion. Also what does "react twice" means? Is that really the same thing as crossing the TS twice?)
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
- The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.
- It assumes that the collision between molecules are completely elastic.
- The theory assumes that even when the reactants and products are not in equilibrium with each other, the activated complexes are in quasi-equilibrium with the reactants.
- It is assumed that the flux of activated complexes in the two directions are independent of each other.
- The theory assumes that each intermediate is long-lived enough to reach a Boltzmann distribution of energies before continuing to the next step.
- Transition state theory is also based on the assumption that atomic nuclei behave according to classic mechanics.
- The theory assumes the reaction system will pass over the lowest energy saddle point on the potential energy surface.
- The assumption that the trajectory will pass through the saddle point is not applicable in reality as the probability of the reaction passing the saddle point is very small.
- It assumes that the reaction does not recross the saddle point but as seen in the last two systems above, it can recross in reality.
(Fv611 (talk) 14:23, 9 June 2017 (BST) Ok. Should have referenced your claims. Could have expanded more on what the assumption of classical behaviour implies. The treatment of recrossing is a key point, it could have been highlighted more. Also you don't discuss rate prediction at all.) Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
| Reaction | Enthalpy |
|---|---|
| F + H2 | Exothermic |
| H +HF | Endothermic |
When the distance AB (HF) is small, the potential energy is lower compared to the distance BC (HH).
(Fv611 (talk) 14:23, 9 June 2017 (BST) You mean "compared to when BC distance is small")
The literature states that the bond strength of HF (565 kJ/mol) is larger than HH bond strength (432 kJ/mol) which shows that there will be an overall larger stabilization and release of energy with the formation of the HF bond compared to the second reaction.
Locate the approximate position of the transition state
rHF = 1.81 A
rHH = 0.745 A
Report the activation energy for both reactions.
Energy of transition state = -103.3 kcal/mol
Energy of HF and H = -133.9 kcal/mol
Energy of H2 and F = -103.9 kcal/mol
Therefore the activation energy of the reaction is,
Reaction 1: Ea = 0.6 kcal/mol
Reaction 2: Ea = 30.6 kcal/mol
ΔrH = -30.0 kcal/mol
(Fv611 (talk) 14:23, 9 June 2017 (BST) For all three questions above, you provide absolutely no justifications for the values you report. You need to show your results, otherwise the only option is to trust you did the work, and most people wouldn't.)
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
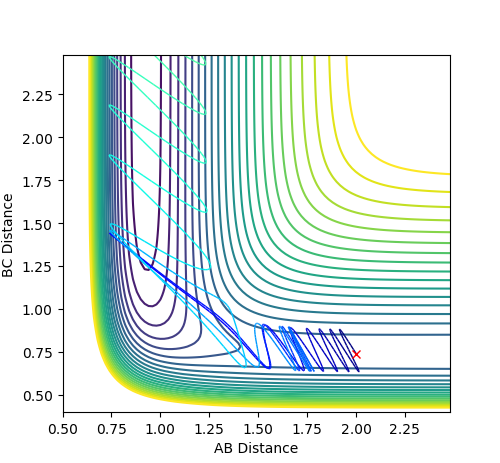
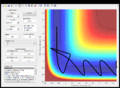
From the internuclear momentum vs time graph it can be seen that HH goes from a highly oscillating graph to a straight line whereas the opposite occurs to the HF. This means when the energy is conserved it is converted to vibrational energy which are displayed by the oscillating part of the graph. The HF bond forms and increases its vibrations whereas the opposite occurs for HH.
This could be proved experimentally by infrared chemiluminescence.
(Fv611 (talk) 14:23, 9 June 2017 (BST) Not enough discussion. What does "when the energy is conserved" mean? Energy is always conserved.) Setup initial conditions starting at the bottom of the entry channel, with very low vibrational motion on on the H - F bond, and an arbitrarily high value of pHH above the activation energy (an H atom colliding with a high kinetic energy)
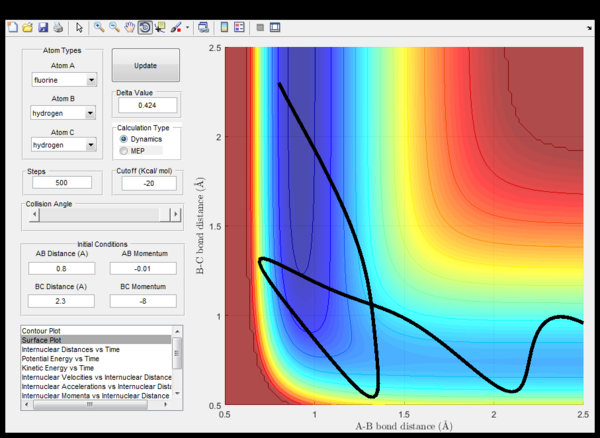
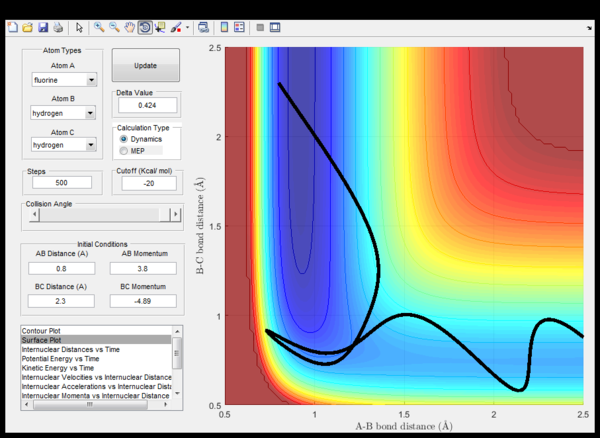
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The rule states that for reactions with late transition states, the vibrational energy is more efficient than transational energy in order to promote the particular reaction.
In endothermic reactions, using the Hammond's postulate, it could be predicted that the transition state is closer in energy to the products of the reaction. This is shown in the second screen shot above with low p(HH) where it requires less energy for the reaction to proceed as energy is stored in the vibration of HF. Whereas, in exothermic reactions, the transational energy dominates for the reaction progression. Therefore the rate of an exothermic reaction could be increased more with heating whereas an endothermic reaction would prefer IR radiation to increase bond vibrations.
(Fv611 (talk) 14:23, 9 June 2017 (BST) As you didn't number your figures, it is very hard to follow your discussion. You actually confuse the reaction directions as you keep the identity of the A, B , C atoms and change the initial distances, instead of doing the opposite. Also you don't reference the rules.)