MRD:sm6416

H₂ + H Exercise 1

Transition State Dynamics

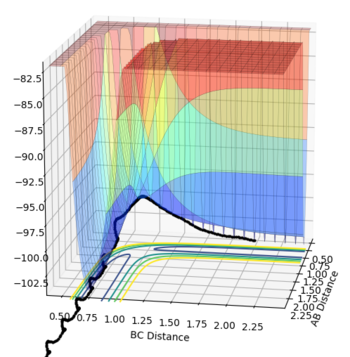
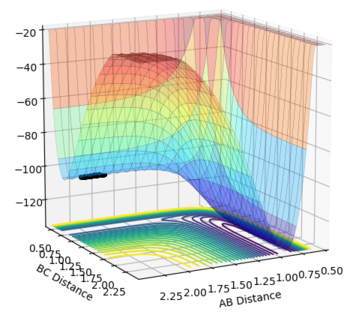
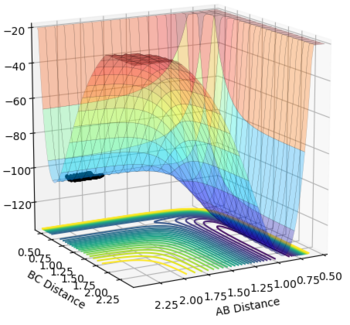
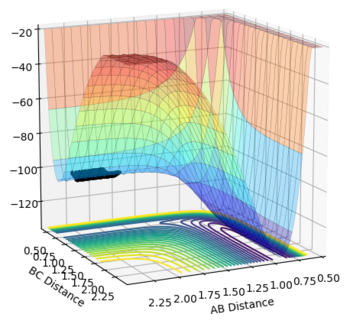
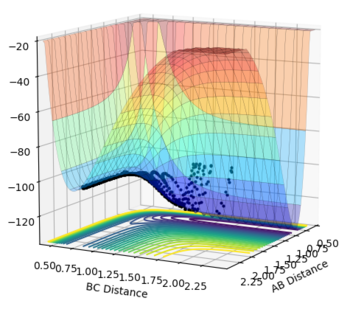
The transition state is the stage in a reaction coordinate that must be passed through in order for a reaction to occur and occurs at a saddle point, as shown by the numerous surface plots on this page. The first derivative highlights the positions along the reaction coordinate where the gradient equals zero. However, in order to determine if a saddle point ensues, the second derivative of the gradient must be taken. A saddle point is only present if the second derivative > 0.

This part is not true. Firstly, you need to check from two directions to determine whether a point is a saddle point. Secondly, saddle point is a minimum from one direction and a maximum from another direction. Please check the Pringles in the figure. 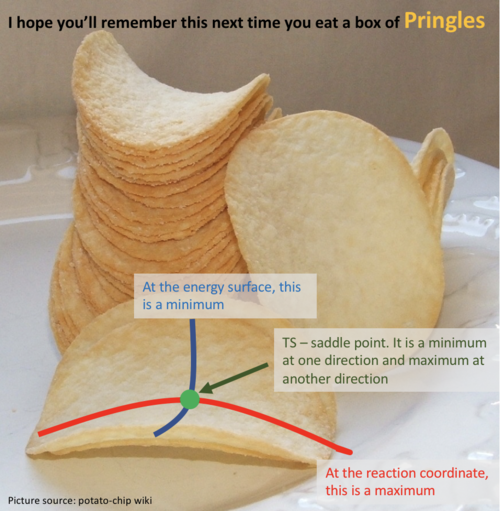Finally, second derivative > 0 with first derivative = 0 doesn't give you a saddle point. But what does it give you? I think you implied a maximum. But is it true?--Sw2711 (talk) 16:10, 31 May 2018 (BST)

Another way to think of the transition state is by thinking of the tangent that can be formed at the transition state itself. This tangent will follow the reaction coordinate profile and therefore is expected to be a maximum, where the gradient = 0. A line can be drawn to the normal of the tangent at the selected transition state. This path would show a minimum, where the gradient again = 0, at the intersection of the tangent with normal if the transition state has been correctly identified. It is only in this scenario that a transition state can be determined as one. This part. I think you are sort of describing a saddle point, But somehow, you are thinking it is the only scenario. Here, I'd like to reassure you that a TS point is a saddle point. It is always true. A saddle point is a minimum at one component and a maximum at another component. This is from its mathematical definition. So this is always true as well. In molecular reaction, it is always a maximum along the reaction coordinate and a minimum along the potential well (i.e. the moorse potential). But the diagonal of AB/BC doesn't always pass the maximum or minimum of either component. It is at this case, because the product H+HH is the same as the reactant HH+H in the system. So it is symmetrical. --Sw2711 (talk) 16:10, 31 May 2018 (BST)

Please also watch this video to understand how you can determine a saddle point. link--Sw2711 (talk) 16:10, 31 May 2018 (BST)

Locating the Transition State

Good--Sw2711 (talk) 16:13, 31 May 2018 (BST)

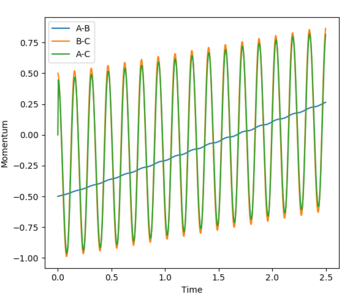
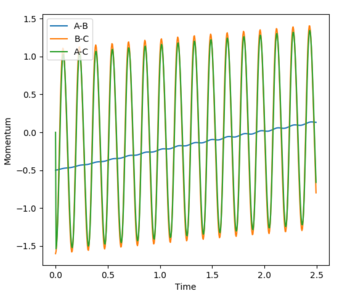
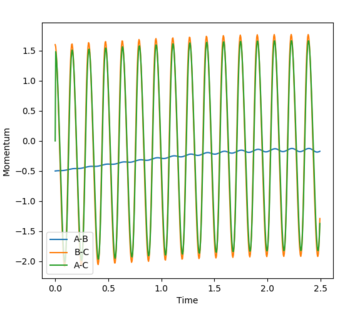
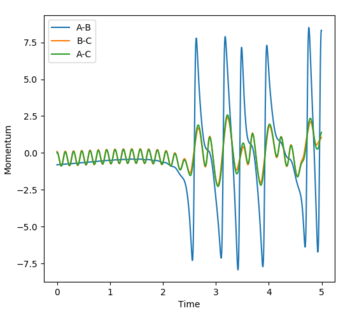
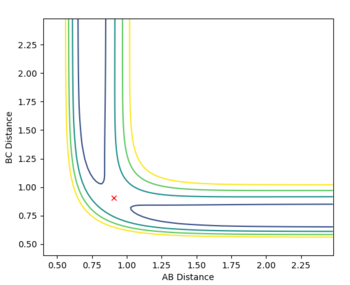
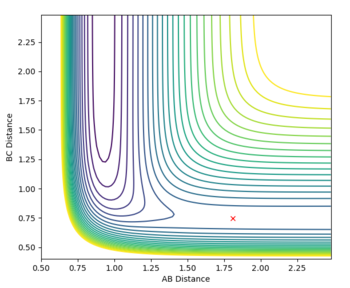
The transition state was determined through iterations of both r₁ and r₂ which resulted in the smallest displacement of momenta along with no displacement as shown by the contour plot. This method determined at r_ts = 0.907743.

Contour plot demonstrating r_ts = 0.907743 as a result of no fluctuations from the initial input, hence the complex is at the transition state.

Momenta vs Time plot demonstrating minimum, and almost zero, momentum at r_ts = 0.907743.

Internuclear Distance vs Time plot demonstrating no fluctuations in distance and hence r_ts = 0.907743.

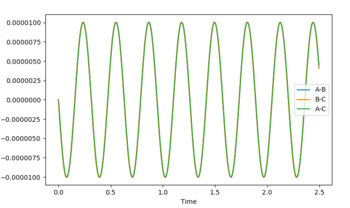
Reaction Path

The minimum energy path (MEP) is defined as the lowest path the reaction must follow to form the products and is the downhill motion from the transition state. It can be applied in both directions in the case in question. The MEP views the system as static as it resets the velocity to zero at each step. Whereas the trajectory is very much dynamic and the momenta is accounted for, this is reflected in the vibrational oscillation of the molecule as it passes along the minimum well towards the products.

I am not sure whether MEP always follow the lowest path to for the Products. Try the very first example in this lab. Compare the MEP and dynamics. Otherwise it is good--Sw2711 (talk) 16:21, 31 May 2018 (BST)

MEP

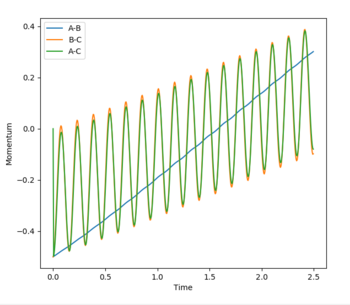
Initial conditions of r₁ = r_ts + 0.01 = 0.917743, r₂ = r_ts = 0.907743 and p₁ = p₂ = 0 for the MEP simulation.

Surface plot highlighting the minimum energy path (MEP), as the reaction returns to the reactants without fully passing through the transition state.

Momenta vs Time plot demonstrating zero momentum, as inputted, and more importantly not change in momentum with running the simulation.

Internuclear Distance vs Time plot showing that the reactants reach the transition state at the interception of r₁ = r₂. r₁ quickly reaches a constant value, namely the equilibrium bond length of the reactant molecule. r₂ increases logarithmically as time progresses, this represents an increasing distance of H_a from H_b-H_c and a continuing loss of momentum.

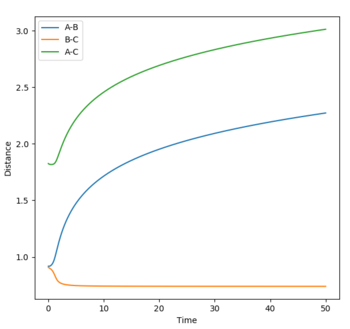
Final values from the MEP simulation.

r₁ = 2.76195

r₂ = 0.75883

These values reflect the minimum trajectory for a successful reaction.

p₁ = p₂ = 0

Dynamic

Surface plot highlighting the minimum energy path (MEP) with oscillation of the reactants, as the reaction returns to the reactants without fully passing through the transition state. It is therefore evident that the momentum as a result of the vibrational oscillation does not provide enough energy to proceed to the products.

Momenta vs Time plot demonstrating the momenta associated with the oscillating reactants.

Internuclear Distance vs Time plot showing that the reactants reach the transition state at the interception of r₁ = r₂. r₁ quickly decreases and oscillates about a constant value, namely the equilibrium bond length of the reactant molecule. r₂ increases linearly as time progresses, this represents an increasing distance of H_a from H_b-H_c with a constant momentum.

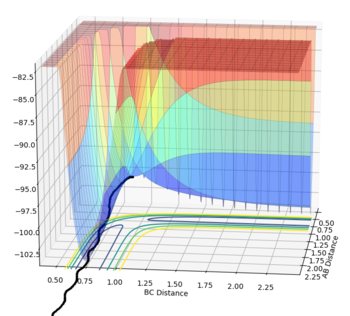
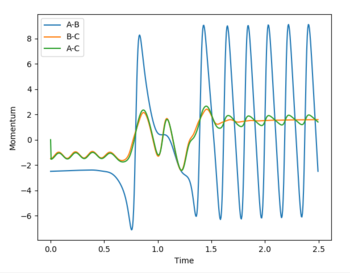
Dynamic simulation final values

r₁ = 10.0045

r₂ = 0.75883

p₁ = 2.48523

p₂ = 1.29898

p_(average) = 1.90409

With r₁ = r_ts and  r₂ = r_ts + 0.01 would simply produce the same answer however the values would be flipped to the other distance. In other words r₁ = 0.75883 and r₂ = 10.0045 would be the output values.

Maintaining the final trajectories as calculated from the dynamic simulation and reversing the sign of the momenta, the reaction proceeds in the reverse direction to the products.

Reactivity of Trajectories

These simulations are restricted by the number of steps the program can handle, however a sound understanding of the reaction can be appreciated and the reactivity of each scenario can be determined appropriately.

Simulation	p1	p2	Energy (kcal/mol)	Reactivity	Evidence	Description
1	-1.25	-2.5	5.03500	Reactive		The reactants proceed through the transition state and to the products. The r2 distance decreases to the equilibrium bond length, whilst r1 simultaneously exhibits dissociation and increases beyond the scope of the graph. The small momenta attributed to the reactants is reflected in the vibrationally oscillating products, with a small amplitude.
2	-1.5	-2.0	3.62879	Unreactive		This is unreactive as the oscillating reactants reach the transition state point and r1 immediately returns to the initial bond length, whilst r2 continues to increase as it moves away from the H2 molecule.
3	-1.5	-2.5	5.13738	Reactive		This simulation shows a reactive pathway that is very similar to simulation 1, however due to the greater momenta associated with the reactants, as inputted, vibrational oscillations with a greater amplitude can be observed.
4	-2.5	-5.0	9.86678	Unreactive		Initially seen here are oscillating reactants with a very large amplitude. However, this simulation is unreactive despite the reactants going through the transition state and towards the product, they return to the initial reactants.
5	-2.5	-5.2	11.80780	Reactive		Like simulation 4, this simulation shows a large oscillating amplitude, whereas in this scenario after passing through the transition state, the products are completely obtained. The slight increase in the p2 momentum can be seen to result in the products.

Transition State Theory

Transition State Theory (TST) assumes a quasi-equilibrium between reactants and the transition state. The reaction between the transition state and products is irreversible and therefore is unable to return to the reactants, however many of the surface plots on this page show the complete antithesis of this highlighting a dichotomy between theory and experimental. TST further assumes that fluctuation as to whether the transition complexes go towards reactants or products are independent of each other and hence the rate of one can not be determined by the other.

TST is an excellent qualitative tool and can identify the enthalpy, standard entropy and standard Gibbs energy of activation. Despite this, it the method is unable to accurately determine these true values in line with experimental results as doing so would require a deep understanding of the potential energy surface of each reaction. Therefore, TST under estimates the reaction rate in comparison to the experimental values. When TST was developed in 1935 a lack of adequate computer software to accurately map potential energy surfaces with the relative quantum mechanical contributions to determine the distribution of electron density, unlike there is today. Hence resulting in a less accurate and longer method to map these surfaces for each reaction.

Overall good. Just one minor point: I think the term ‘equilibrium’ is not very applicable here. ‘equilibrium’ is mainly used in statistical thermodynamics. So like…thinking about a reaction A+B<=>C. Statistically speaking there is 80% molecules in this system reacts from the left to the right and 20% the other way around. (about obviously you should think about more like a Boltzmann distribution ). This reaction has reached an equilibrium. But in terms of your system, there are only 3 atoms. So, it is either one way or the other. --Sw2711 (talk) 16:23, 31 May 2018 (BST)

F-H-H System Exercise 2

Potential Energy Surface Inspection

Energetics

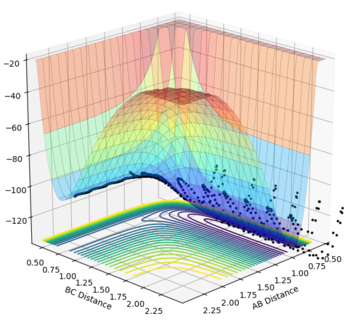
F + H₂ is an exothermic reaction as can be seen from the surface plot, the reaction progresses from a small H-H distance to a longer one, whilst H-F simultaneously equilibriates about the F-H bond length. It can be seen that the products are lower, and hence more stable, in energy than the reactants.

F-H + H is simply the reverse reaction that passes through the same transition state, hence this reaction is endothermic with the products being higher in energy than the reactants. There is an overall gain of energy.

With this information in mind, the F-H bond is more stable and thus stronger than the H-H bond. The main factors to this argument is the greater electronegativity of F leading to a stronger contribution to the bond than the molecular orbitals. Hence the overlap of molecular orbitals is a weaker factor in the bond strength.

This part is good--Sw2711 (talk) 16:24, 31 May 2018 (BST)

Surface plot highlighting the energetics of the F-H-H system.

Surface plot highlighting the energetics of the H-H-F system.

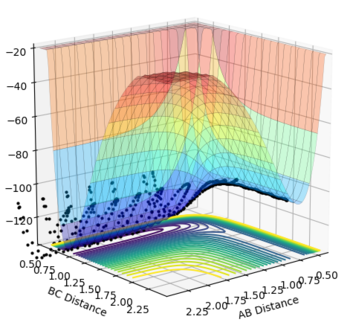
Transition State

Good--Sw2711 (talk) 16:25, 31 May 2018 (BST)

Hammond's postulate aids in finding the transition state; it relates the composition of the transition complex to either the reactants or products for an early or late transition state respectively. In the scenario under investigation for F + H₂ an early transition state is present as the reaction is exothermic in this direction, hence the transition state resembles the reactants more.

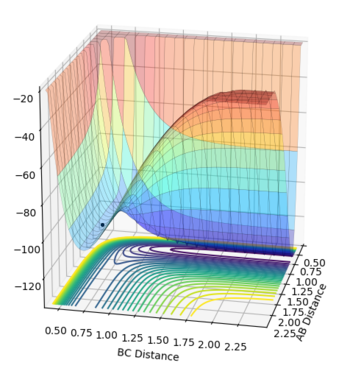
This guidance proved useful in determining the transition state complex at r₁ = F-H = 1.810076 Angstrom and r₂ = H-H = 0.74634 Angstrom, as can be seen from the surface and contour plots below showing the absence of displacement to either reactants or products. Furthermore the Momenta vs Time plot indicates a very small momenta of the overall system, without any deviation or substantial change in the momenta.

Contour plot demonstrating r_ts as a result of no fluctuations from the initial input, hence the complex is metaphorically sitting on the transition state.

Momenta vs Time plot demonstrating minimum, and almost zero, momentum at r_ts.

Activation Energy

Good--Sw2711 (talk) 16:25, 31 May 2018 (BST)

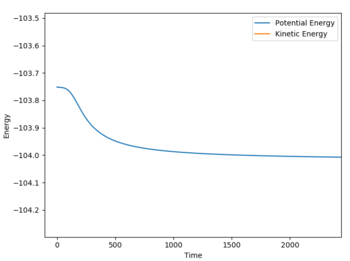
The activation energy for the exothermic reaction was calculated through a 500000 step MEP simulation with input values of r₁ = 1.820076, r₂ = 0.74634 and p₁ = p₂ = 0. It was required that after following the minimum energy path, the gradient of the line signifying the reactants was constant.

The activation energy is reported at +0.258 kcal/mol for the exothermic process.

Energy vs Time graph highlighting the activation energy of the exothermic reaction.

The activation energy for the endothermic process was determined with the following parameters: r₁ = 1.800076, r₂ = 0.74634, p₁ = p₂ = 0 with 250000 steps. These parameters 'tipped' the reaction towards the FH + H reactants. The reported activation energy was +30.277 kcal/mol.

Energy vs Time graph highlighting the activation energy of the endothermic reaction.

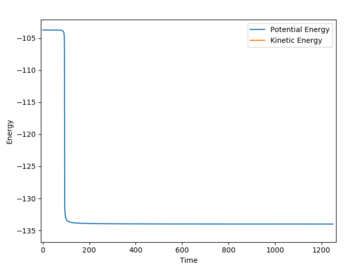
It can hence be seen that the exothermic reaction of F + H₂ --> F-H + H only requires a small activation energy as the products are substantially more thermodynamically stable than the reactants.

Reaction Dynamics

In this exothermic reaction, the potential energy is mainly converted into vibrational energy of the FH bond, along with heat. As a result of this vibrational energy in the FH bond, vibrational levels above the ground state will become partially populated. In this manner, by recording an IR spectrum of the products, the main F-H will be observed alongside an overtone, with the intensity of this overtone relating to the population of this vibrationally excited state, which can then be used to determine the vibrational energy in the bond itself.

In this same vein, IR chemiluminescence can be employed to yield the same result by measuring the wavelength, and subsequent vibrational energy of the FH bond, of the infrared light that is irradiated from the products and being excited with incident light.

Calorimetry is not a suitable method to measure the vibrational energy of the bond, as this method merely takes an average of both translational and vibrational energies present in the system.

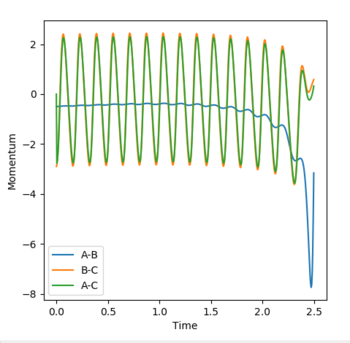
As the momentum closes towards the boundaries of -3 < p < +3, the system passes through transition state but returns to reactant well. This shows that the excess momentum of the system in the product well is sufficient to overcome the high activation energy and return to the thermodynamically unfavourable reactants.

This part is good--Sw2711 (talk) 16:28, 31 May 2018 (BST)

The following parameters were employed for all simulations r_FH = 2.3, r_HH = 0.74 with 500 steps calculated.

Simulation	pHH	pFH	Surface Plot	Momenta vs Time Plot	Observations
1	-2.5	-1.5			This trajectory results in a successful reaction as seen from the surface plot; the reactants proceed through the transition state and continue into the product well, whilst continually oscillating as a result of the momentum gained.
2	-0.5	-0.5			This momentum does not proceed to a reaction. Through the dynamic animation it can be seen that the HH molecule does not possess enough momentum to translate towards F. Therefore the system does not translate out of the reactant well, as seen in the surface plot, since there is not enough energy to overcome the activation energy. The momenta plot simply shows a small up trend, this is expected due to the long range electrostatic force of attraction between F and HH, resulting in a slight increase in the HH vibration velocity. There is no drastic change in the momenta of either F or HH that would otherwise indicate the occurrence of a reaction, as seen in simulation 1 above.
3	+0.5	-0.5			This simulation shows an unreactive path, as can be seen from the surface plot, the system remains in the reactant well as it does not overcome the small activation energy for the exothermic reaction to proceed. As in simulation 2, the momentum amplitude of the oscillating HH remains constant however the overall momenta of the system increases due to a slight translation towards F, thus increasing electrostatic attraction forces resulting in this slight overall momenta increase.
4	-1.6	-0.5			This simulation is very similar to simulations 2 & 3 in that the system remains in the reactant well as there is not sufficient energy to overcome the activation energy. However as a result of the greater HH momentum, the oscillation amplitude is greater than both simulation 1 & 2.
5	+1.6	-0.5			Firstly, this simulation is unreactive as can be seen from the surface plot. In comparison to simulation 4, HH momentum sign has been changed and as a result this has led to not only a greater oscillating amplitude but also a larger translation towards F. So much so in the latter than the Momenta vs Time plot shows an increase in FH oscillation momentum as the electrostatic forces of attraction dominate due to the reduction in internuclear distance.
6	-2.9	-0.5			This is the first reactive simulation observed, as can be seen from the surface plot and the drastic change in the momentum of FH. Evidently, there is sufficient energy to pass through the transition state complex and towards the reactants.
7	+2.9	-0.5			This simulation is indeed similar to that of simulation 6 however, the change of sign for the HH momentum again results in a greater translation towards F and consequently the system passes through the transition complex shown by the surface plot and Momenta vs Time plot. However after a single oscillation, FH dissociates and the system returns to the reactant well with HH possessing a greater momentum. This scenario could be as a result of the HH momentum being too high and thus providing sufficient activation energy to proceed in the endothermic direction. This is surprising as the exothermic reaction elucidates more thermodynamically stable products.
8	+0.1	-0.8			With a mere 60% change in FH momentum and a minimum HH momentum, the system can be seen to react fully, without returning through the transition state. The Momenta vs Time plot further shows a noticeable change in the AB momentum, which corresponds to FH. Despite the oscillations not being regular, it can be noted that the amplitudes are relatively of the same size and show no signs of regressing. This information highlights that the overall the FH momentum dominates the reactivity of the system and has a large weighting to overcoming the activation energy. It can be thought that the increase in momentum aids in allowing a closer distance of F & H, where electrostatic attraction forces will prevail.

Polyani's Empirical Rules

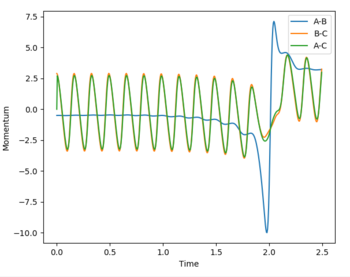
The reactive trajectory for the FH + H was determined with the following parameters: r_FH = 0.9, r_HH = 2.3, p_FH = 6.5, p_HH = -1.5. The plots below highlight that these parameters lead to a reactive trajectory.

Surface plot showing the reactants pass through the transition state and enter the product well without returning through the transition complex. This trajectory is therefore reactive.

Momenta vs Time plot indicating the substantial loss of momentum of FH, indicating dissociation, with the simultaneous gain in momentum of HH, indicated by the orange line.

Internuclear Distance vs Time plot showing a successful reaction. The HH distance vibrationally oscillates about the equilibrium bond distance, whereas the F-H distance increases linearly as a result of F translating away from H₂.

Contour plot highlighting similar information to the surface plot above in that the system stably occupies the product well without returning through the transition complex.

In order to react, a system must overcome the activation energy, the energy to achieve this is supplied by either translational or vibrational energy. As reported by Polanyi's Empirical Rules, a late transition state, one that resembles the products more as stated through Hammond's Postulate, is achieved through a greater contribution from vibrational energy enabling the activation energy to be overcome. The opposite is true for an early transition state which is promoted by a greater contribution from translational energy.

The F + H₂ system is exothermic, thus an early transition state is present. Therefore this is promoted with higher translational energy being able to overcome the activation energy, hence p_FH would contribute to the translational energy whereas p_HH relates to the vibrational energy of the HH bond.

On the other hand, the FH + H system is endothermic and relates to a late transition state as dictated by Hammond's Postulate, requiring high vibrational energy of the FH bond to overcome the activation energy. In this scenario, p_FH refers to the vibrational energy and p_HH the translational energy.

This part is good.--Sw2711 (talk) 16:28, 31 May 2018 (BST)