MRD:sjh115
Molecular Reaction Dynamics Computational Lab
EXERCISE 1: H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minimum and transition structures can be distinguished using the curvature of the potential energy surface.
For a minimum in the potential energy surface the gradient is 0. For a transition structure the gradient of the potential energy surface is also 0. However the difference between the two is that the transition structure is a saddle point, so it is a minimax point. So in order to distinguish the two points the second derivative test must be used;
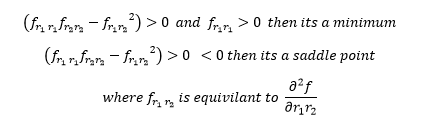
(Good use of the second derivative test. But I don't know what you mean by saying that the transition structure is a saddle point, so it is a minimax point. Should have elaborated a bit more on that for clarity. Je714 (talk) 11:29, 15 May 2017 (BST))
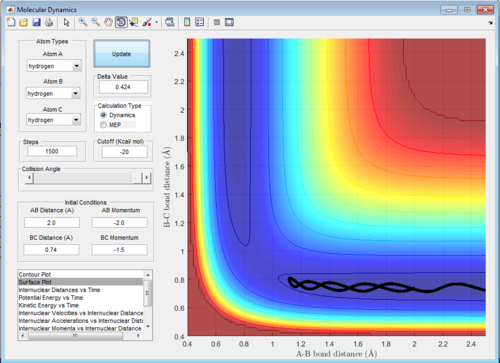
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
My best estimate of the transition state is at 0.908 Angstroms from both the terminal hydrogen's to the central hydrogen, so the transition state is symmetric as all the atoms are the same. The transition state is the point where the internuclear distances do not fluctuate with time as it is a metastable state so the bond lengths won't fluctuate. So on the internuclear distance vs time graph the line will be flat as shown in figure 2.
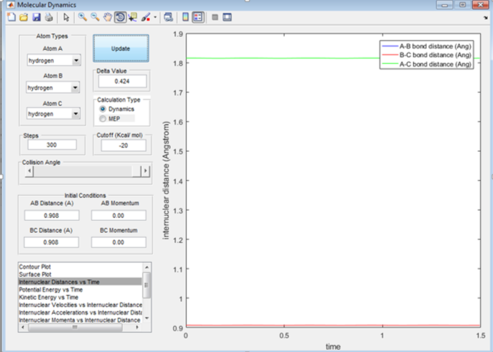
Comment on how the mep and the trajectory you just calculated differ.
The mep calculation differ to the dynamic one as the reaction path does not give deviations from the minimum of the potential well. The dynamic calculation includes vibrations, interactions with the environment and other factors that in reality cause the reaction path to not directly follow the minimum potential energy path. If the calculation is set up such that the final positions are set as the starting positions then the reverse reaction takes place, the products goes to the reactants.
(Those are just observations. How is the MEP calculation done differently from a Dynamics one so that the minimal of the potential well is followed at every step? (Hint: it has to do with the velocities -- and therefore momenta of the atoms at every time step). Je714 (talk) 11:32, 15 May 2017 (BST))
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
[[File:MRDgraph7sjh115.PNG|thumb|centre|236x236px]
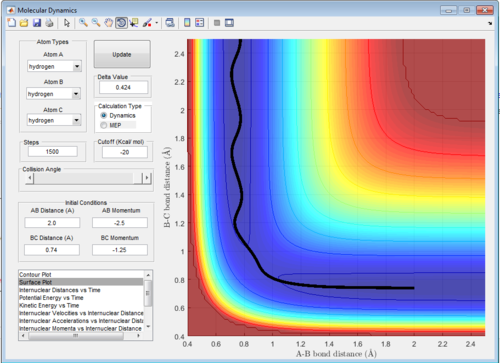


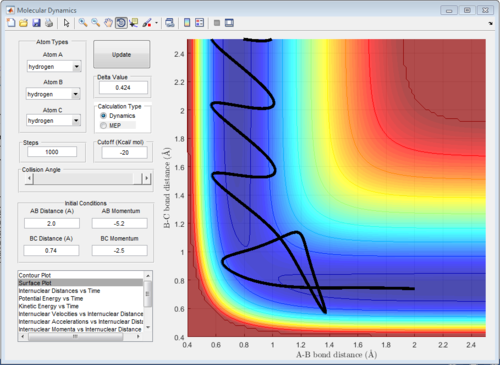
The reason why Figure 5 and 7 results in no reaction is that the the approaching atom has too much translational energy and too little vibrational energy and thus bounces back and doesn't react. As the transition state is symmetric is transition state requires both enough vibrational and translational energy, not lots more of one and not much of the other. As Polanyi’s empirical rules state that vibrational energy promotes reactions with late transition states and translational energy promotes reactions with early transition states this scenario is kind of a symmetric interpretation of Polanyi's rules.[1]
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
It assumes that the atoms behave according to classical mechanics. So if the particles collide with enough energy then the reaction can take place. However, quantum mechanics has shown that the particles don’t need to have sufficient energy to react as they can tunnel through an energy barrier of finite height. Transition state theory predicted rates of reaction rate values will be slightly lower than experimental values as they fail to take quantum tunnelling into consideration. However, another assumption is that the trajectory follow the path of the minimum potential energy. In reality the trajectory is less regular and goes over higher energy paths. This results on the predicted rate being lower than the experimentally determined rate. This second effect is likely to outweigh the first effect resulting in the second conclusion.[2]
(I think that's what you're aiming for with your last point, but I'll just leave it here for completeness: that's called barrier recrossing and is actually the biggest point to be made here, since it's actually what you observe in at least two of your previously discussed trajectories. Although not wrong, the QM limitation isn't really disproven here. Je714 (talk) 11:34, 15 May 2017 (BST))
EXERCISE 2: F - H - H system
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

The reaction to form F + H2 is exothermic as from the energy surface the shows that the products are lower in energy than the reactants. This shows that the bond in HF is stronger than H2 as HF is the more stable product so more energy is required to break the bond. The reverse reaction is then endothermic as the energy of the products in this reaction are higher in energy than the reactants, so the energy required to break the HF bond and isn’t recouped on the formation of the H2 bond.
Locate the approximate position of the transition state.
For F H-H system the F-H distance is 1.810 Angstroms and the H-H distance is 0.745 Angstroms. For the H H-F system the F-H distance is 0.745 Angstroms and the H-H distance is 1.810 Angstroms.

(How did you find this? Made use of Hammond's postulate perhaps? Or just brute force searched over the whole PES? I presume not :D Je714 (talk) 11:36, 15 May 2017 (BST))
Report the activation energy for both reactions.
The activation energy of a reaction is the difference in the energy of the reactants and the transition state. For the F H-H system the activation energy is -0.2 Kcal/mol which is -0.8368 kj/mol. For the H H-F system the activation energy is 30.2 Kcal/mol which is 126.3568 kj/mol.
How did you achieve these numbers? You need to explain your reasoning and provide some evidence in the form of screenshots. Also, are you sure that an activation energy is negative? That doesn't really make sense. Je714 (talk) 11:38, 15 May 2017 (BST)
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
Since energy is conserved it must be converted from one form to another, i.e. potential to kinetic. In the case of an energy releasing reaction, i.e. an exothermic reaction, energy is converted from potential chemical energy to kinetic energy. This is done by breaking bonds releasing chemical potential energy to give the surrounding particles kinetic energy. This rise in average kinetic energy results in a rise in temperature. This rise in temperature is how we will experimentally confirm this mechanism experimentally. This is done by calorimetry, ie using a thermometer. The energy equals the mass multiplied by the specific heat capacity multiplied by the temperature change. The kinetic energy can be broken down into increase in vibrational and translational energy. The initial reactants have lower vibrational and translational energy, this can be seen as the lines are more dense and don't go very far up the sides of the reactant channel compared to the product channel. This is one way to show this increase in overall kinetic energy of the particles in the model. As shown below in figure 11.

(Good discussion. It's better to write the mathematical formula for the energy change with temperature, instead of spelling it out in English. Je714 (talk) 11:40, 15 May 2017 (BST))
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
The form in which energy is distributed can affect the efficiency of a reaction. This can be explained using Polanyi’s empirical rules, which states that vibrational energy promotes reactions with late transition states and translational energy promotes reactions with early transition states. So if the transition state is early and the reaction mainly has the vibrational form of energy then it may be very slow or might not have enough energy to react at all. Polanyi’s rules can be rationalised by thinking about what an early transition state is like; the approaching atom needs the extra translational energy to collide with enough force to break the existing bond and form new one. However, in a late transition state the original bond is more broken than the new bond is so this state requires vibrational energy to break the bond. So the transition states require the right kind of energy to optimise reaction efficiency.[1]
(Yes, those are the Polanyi's empirical rules. I miss some examples from previous trajectories for each case, to show that you've understood them and you're able to apply them. Je714 (talk) 11:41, 15 May 2017 (BST))
References
(1) Bowman, J. M. 2012, 4, 4–7.
(2) Atkins, P. W.; DePaula, J. Physcial Chemsitry; OUP Oxford, 2014; Vol. 10th.
