MRD:scc215 phycomp
Molecular Reaction Dynamics : Application to Triatomic system
Introduction
In this experiment, two triatomic reaction systems was investigated for kinetics: the H2 + H system and the F + H 2system. Both of them have their reaction trajectory and kinetics mechanism as follows. For the first part of write-up, the kinetics of the system was supposed to obey the predictions from Transition State Theory but due to the involvement of the low molar mass molecule, the quantum tunneling effect has created discrepancy from prediction of theory.
For the second part of the experiment, the system was found to obey the Polanyi's empirical rules for rate of reactions, and the result could be further applied to explain the unreactive trajectory with sufficient amount of energy.
Part 1 : H + H2 system
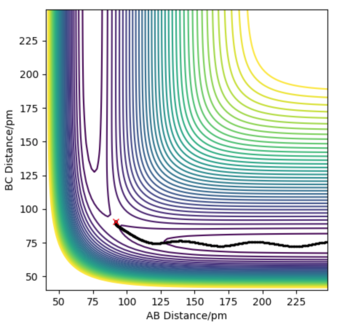
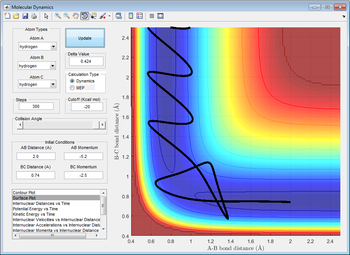
Total Gradient of the potential energy surface at its minimum and possess a transitional structure
As predicted from the potential energy surface, the minimum of total gradient has shown a series of valley floor on the surface and the transition state is also locating on the valley floor. By taking the primary derivative of potential energy with respect to corresponding coordinate , it was showed that the value of for every point along the valley floor, such that the total gradient is always 0 when the gradients are attaining their minimum.
(Fv611 (talk) 11:08, 30 May 2017 (BST) Not sure about what you mean by "the minimum of total gradient". Also the gradient is not zero for every point along the valley floor, unless you specify that you are considering all coordinates but the reaction coordinate.)
Distinguish the minimal and transitional structures from the curvature of potential surface
The z-axis is the potential energy of the whole system, which the system always follows a reaction pathway constructed by the minimum valley of potential energy. As mentioned above, taking the secondary derivative of potential energy with respect to the corresponding coordinates would be letting the minimum of energy to be found out. The transitional structure is found out by the local maximum of the valley floor since it should be the point with highest potential energy within the reaction trajectory. The position of transition state was further supported mathematically, through a primary derivative of zero and the second derivative . For local maximum, before reaching maximum and after the maximum.
(Fv611 (talk) 11:08, 30 May 2017 (BST) The system does not always follow the minimum valley. If it did, would you observe bond vibrations? The definition of the TS is correct, but you don't explain how to distinguish it from the minimum.)
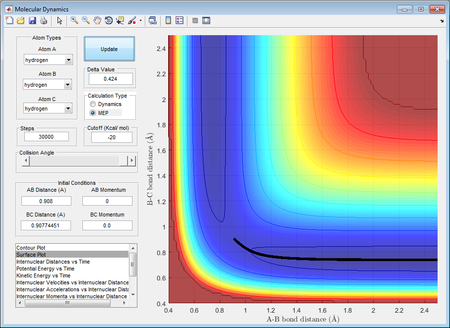
Estimation on transition state position


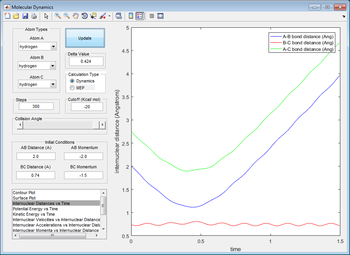
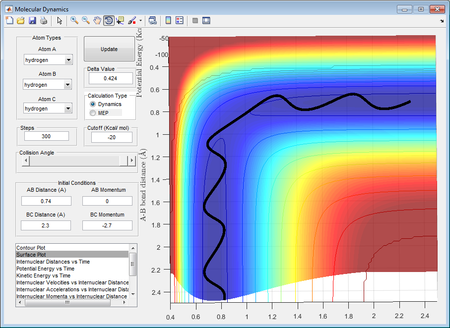
The best estimated transition state position was rAB = rBC = 0.90774451 Å. The position was estimated and reported since it was known that the internuclear distances was known to be constant when the system is at transition state and from the diagram it was shown that there was oscillation yet it was barely observable from the "Internuclear distance vs Time" graph. The evidence of its oscillation could be shown from the "Internuclear momenta vs Time" graph.
(Fv611 (talk) 11:08, 30 May 2017 (BST) That's a lot of significant figures - do they mean anything? You do not explain why you expect no oscillations at the TS.)
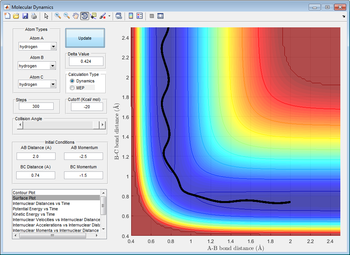
Comparison between minimum energy path (mep) and calculated dynamic trajectory
From the comparison between mep and the calculated dynamic trajectory, it was discovered the mep estimated is a straight line without any oscillation whereas the dynamic trajectory had shown a constant oscillation throughout the process of moving from transition state to product.

The difference between mep and dynamic trajectory could be justified through the their calculation method. In calculation of dynamic trajectory, the trajectory always follows the minima of the valley floor of potential energy, and this would take account into the vibrational contributions such that the trajectory oscillates. On the other hand, the MEP was estimated by resetting the velocites of atoms to 0 after every cycle of oscillation such that the vibrational contribution is excluded.
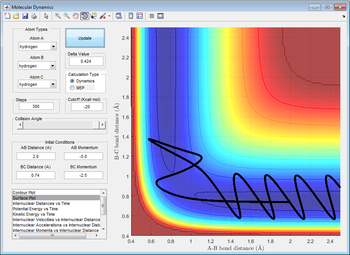
Determination of Reactive and Unreactive Trajectories
Main assumptions made by Transiton State Theory and Comparison towards experimental results
Transition State theory (TST) was based on classical mechanics and had made assumptions for the separation of electronic and nuclear motions, and also suggests that distribution pattern is similar to Maxwell-Boltzmann distribution. In addition to the two above, two more unique assumptions was made[1] : reactants crossing the the transition states towards the product side could not reverse their movement, and the movement within transition state should be treated independently from other motions and considered and translation along reaction coordinate (a.k.a. rotational movement neglected). For reactions involving small molar mass, a further assumption of no quantum tunneling effect is made.[2]
Hence by comparing the results with the prediction applying the original TST, the major discrepancy between our experimental results and TST occurs when the reactions trajectories start to move forth and back across the transition state for twice, which contradicts with its fundamental assumption of one-way movement of reactant along reaction coordinate. This is due to failure in application of quantum mechanical tunneling factor to TST, which is essential for accurate predictions on reactions involving low molar mass like this one.
It is also found not possible to calculate the numerical value for rate constants since literature has pointed out that the value can't be calculated without an accurate reaction concentration provided[3]. Thus it is not possible to calculate a numerical value in this experiment even the kinetics mechanisms are given.
Part 2: F-H-H System
PES Inspection
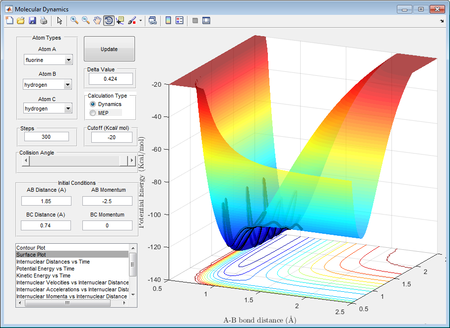
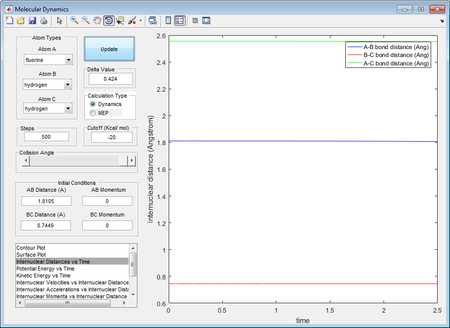
Through inspection on potential energy surface of the system, it is determined that F + H2 is exothermic while the backward reaction, H + HF is endothermic. This could be justified by literature values of H-F bond and H-H bond, which are 568.6 kJ mol-1 and 436.0 kJ mol-1 respectively.[4] As the formation of H-F bond releases more energy than that need to break a H-H bond the reaction is considered to be exothermic, and vice versa.
Location of approximate transition of the transition state
Hammond's Postulate suggests that the transition state resembles the one closest to itself in free energy. Considering the exothermic reaction of F + H2 → H + HF, the transition state have much smaller energy barrier from reactant side than that of product side. Therefore, the transition state has shown rHF = 1.8105 Å and rHH = 0.7449 Å which is nearly identical to normal H-H bond length.
Activation energy of both reactions
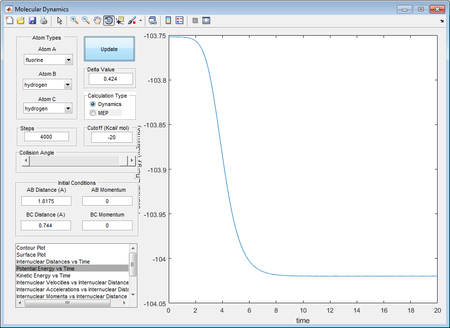
As displayed through the potential energy vs time graph, the value of potential energies are as follows :

Potential energy for transition state: -103.752 kcal mol-1
Potential energy for H2 + F : -104.053 kcal mol-1
Potential energy for H + HF : -134.55 kcal mol-1
Activation energy for forward reaction is 0.301 kcal mol-1
Activation energy for backward reaction is 30.8 kcal mol-1
Reaction Dynamics
Reactive Trajectories and mechanism of releasing reaction energy

As shown in the picture on left, a reactive trajectory of F + H2 was defined.
(Fv611 (talk) 11:08, 30 May 2017 (BST) You should really think about numbering your figures, as their position depends on the layout/size of browser window)
By law of conservation of energy, the internal energy of the atom-diatomic system is constant at all time. Therefore, no energy is assumed to loss to surroundings such that the momenta pFH creates an impact to the H-H bond and has transferred the translational energy to a vibrational energy to the bond, which ultimately cause the bond to break after vigorous vibrations. This could be supported by the "Internuclear momenta vs time"
To further support the hypothesis using experimental observations, another reverse reaction of HF + H should be performed and the energy take in through the reaction should be by measured through calorimetry and then compared with the energy released during the forward reaction.
(Fv611 (talk) 11:08, 30 May 2017 (BST) But how would you specifically test that the energy is transformed in vibrational energy?)
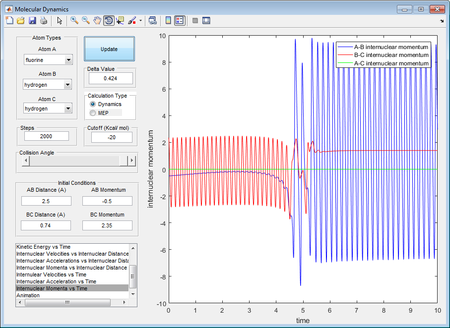
How the distribution of energy affect the efficiency and how the position of transition state influence it
As stated in Polanyi's rules, endothermic reactions such as HF + H in this case mainly have a late transition state, which relies on the energy at vibrational freedom to cross the energy barrier.[5] This was supported by Poliyani's experimental results on reaction rate by a factor of 103 after the transferral of translational energy to vibrational energy[6]. On the contrast, exothermic reactions such as the F + H2 reaction have a early transition state, and relies on mainly translational energy to cross the energy barrier.
(Fv611 (talk) 11:08, 30 May 2017 (BST) You should have related this discussion to examples. Also, there is no discussion on the efficiency of the reaction.)
Conclusions
The kinetics of the above systems has been investigated and it was shown to in line to the scenarios mentioned in the introduction section. The first triatomic system was shown to be in line with TST after the application of a quantum mechanical correction factor [2] while the second system did not show significant discrepancy to theoretical explanations.
References
[1] J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical kinetics and dynamics, Prentice Hall, Upper Saddle River, NJ, 1999.
[2] W. H. Miller, The Journal of Chemical Physics, 1975, 62, 1899–1906.
[3] I. N. Levine, Physical chemistry, McGraw Hill Education (India) Private Limited, New Delhi, 2011.
[4] T. L. Cottrell, The strengths of chemical bonds, Academic Press, New York, 1961.
[5] B. Jiang and H. Guo, The Journal of Chemical Physics, 2013, 138, 234104.
[6] J. C. Polanyi, Science, 1987, 236, 680–690.