MRD:saramalek

H + H₂ system

Gradient of the potential energy surface

QUESTION ONE

dV/dr = 0 (where r= r₁ and r₂ i.e. both partial derivatives = 0) at minimum points and transition structures (saddle points), as a zero gradient represents turning points. A minimum point and saddle point can be distinguished by taking the second partial derivative test; the Hessian determinant ,D, is calculated. If:

D<0 : Saddle point.
D>0 AND the second partial derivative is >0: Minimum point.

Locating the transition state

QUESTION TWO

r_ts=r₁ = r₂ = 0.908 Å

Internuclear Distance VS Time Graph	Analysis
	The graph shows two approximately linear lines i.e. there is no/very little oscillation in energy, therefore it is a saddle point.

Mm10114 (talk) 20:43, 31 May 2018 (BST) The graph looks good. However, you should've explained what steps did you take to find the transition state.

Reaction path

QUESTION THREE

MEP	Dynamic	Comparison
		The dynamic contour plot shows an oscillating trajectory as opposed to the straight trajectory in the MEP contour plot - this oscillations are due to vibrations of the molecule and there are none present in the MEP plot because it is the lowest energy path and thus oscillations are ignored.

Mm10114 (talk) 20:44, 31 May 2018 (BST) Very good observations. But, why is MEP following the lowest energy path? Some cause->effect explanation would be still necessary.

Reactive and unreactive trajectories

QUESTION FOUR

p₁	p₂	Total Energy	Unreactive or Reactive
-1.25	-2.5	-99.018	REACTIVE - The trajectory starts oscillating after it passes the TS, before which it is straight - this shows that the H atom has no vibrational energy as it approaches the vibrating H₂ molecule. This is reactive because it shows the system starting at reactants, passing through the TS and reaching the products.
-1.5	-2.0	-100.456	UNREACTIVE - A approaches and passes the transition state but then recrosses the barrier and goes back to the reactants instead of proceeding towards the products. The trajectory is oscillating before and after the TS, therefore the H atom has vibrational energy.
-1.5	-2.5	-98.956	REACTIVE - The trajectory starts from the reactants, passes through the TS and reaches the products therefore the process is reactive. The trajectory is oscillating from the start, i.e. the H atom is approaching the vibrating H₂ molecule with vibrational energy.
-2.5	-5.0	-84.956	UNREACTIVE - The trajectory starts at the reactants but once it reaches the TS, it recrosses the barrier and reverts back to the reactants. The trajectory is straight before the TS, therefore the H atom has no vibrational energy, but when it returns to the reactants, it is now vibrating - the oscillations are of high amplitude.
-2.5	-5.2	-83.416	REACTIVE - The trajectory starts at reactants, passes the TS and gets to the products. The trajectory starts oscillating after it passes the TS, before which it is straight therefore the product has high vibrational energy. (The oscillations are of high amplitude.)

Transition State Theory

QUESTION FIVE

Assumptions:

Classical mechanics
The transition state will be in (quasi) equilibrium with the reactants
The transition state converts to products every single time

The third prediction means that the theory doesn't account for barrier recrossing and reversion of TS to reactants, which can be seen in the experimental results from question 4. Therefore, the theory overestimates the rate of reaction as it assumes that the transition state always breaks down to form products, i.e. a slower experimental value observed.

However, the first assumption also doesn't apply in all situations. The H atom could tunnel through the activation barrier, a process not accounted for by classical mechanics but by quantum mechanics, as it means that the H atom has wave-like properties (wave-particle duality). Tunneling depends on barrier height, thickness and the mass of the particle, therefore for a (relatively) light H atom tunneling is viable and would thus increase the rate of reactions - in this case the theory underestimates the rate of reaction. For heavier reactants, tunneling would probably be negligible as tunneling wouldn't be favourable, and the classic approach of transition state theory dominates.

Therefore, in the H H₂ system, the experimental rate could be higher than predicted due to tunneling, or lower than predicted due to barrier recrossing; in this case it would seem appropriate that the experimental rate is LESS than the predicted rate as the barrier recrossing effects are more predominant than tunneling due to the requirements for tunneling.

Mm10114 (talk) 20:45, 31 May 2018 (BST) Very good discussion. However, where are these assumptions of TST taken from? You're missing the most important part of the answer - referencing the source.

F-H-H System

PES Inspection

QUESTION SIX

The H-F bond is stronger than the H₂ bond due to the large electronegativity difference between H and F, which polarises the bond introducing strong ionic character. Therefore, the 'F + H₂' reaction will be exothermic (as it includes making a strong bond and breaking a relatively weak one) and the 'H + HF' system will be endothermic (as the strong H-F bond needs to be broken).

QUESTION SEVEN

As 'F + H₂' (the reactants) is higher in energy, it is closer in energy to the transition state, according to Hammond's postulate - i.e. in an exothermic reaction the transition state will resemble the reactants (energetically and structurally). The surface plot below shows the position of the transition state (black dot) - the energy of the transition state is -103.752 kcalmol^-1.

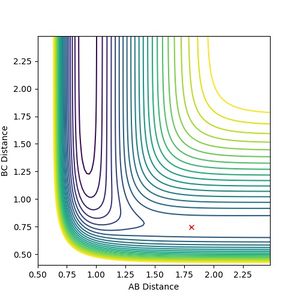
QUESTION EIGHT

The internuclear distance vs time graph below shows the F-H and H-H bond lengths at the transition state; F-H=A-B= 1.810 Å and H-H=BC= 0.745 Å. The plot shows the transition state because the bonds do not oscillate with time i.e. minimum energy.

E_A= E(TS) - E(Reactants)
- Performed an MEP with 500000 steps, with the F-H = 1.9 Å (slightly distorted from TS) and H-H= 0.74 Å. When the reactants are F and H₂:
  - E_A = -103.752 - - 104.008 = +0.256 kcalmol^-1 EXO
- Performed an MEP with 500000 steps, with the F-H = 1.8 Å and H-H= 0.8 Å (slightly distorted from TS). When the reactants are H and H-F:
  - E_A = -103.752 - - 103.877 = -0.125 kcalmol^-1 ENDO

Mm10114 (talk) 20:50, 31 May 2018 (BST) Are you sure this is the correct value for when the reactants are H and H-F? Earlier you have discussed that the H-F bond is much stronger, so breaking it will require energy, thus endothermic reaction. Your value of -0.125 kcal/mol does indicate endothermic reaction, but it does not indicate this is a strong bond to break. It should've alert you, especially that it is half of the magnitude of that you've provided for breaking of H-H bond (although opposite sign). If you would revisit the 3D surface plot, and observe the products/reactants valleys (and look on the Z axis that gives you potential energy) you would see that the difference between the two is much much higher.

Reaction dynamics

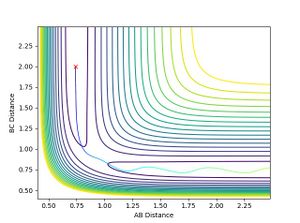
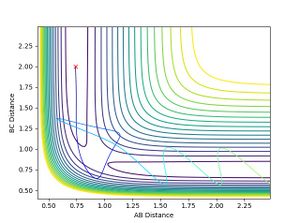
Reactive trajectory of F and H-H

QUESTION NINE

The reaction of F with H₂ is an exothermic reaction therefore energy is released. To conserve energy, this energy is stored in the new F-H molecule as vibrational energy, i.e. it vibrates. This could be confirmed experimentally by measuring IR spectrum of and H-F; the stretching of H-H is IR inactive because it is symmetric.

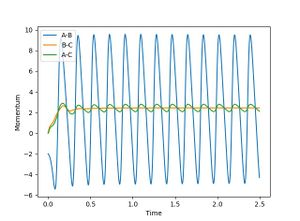
The momentum vs time plot shows that H-H (BC) has constant momentum after the transition state whereas F-H (AB) has an oscillating momentum - this shows that the final H-F molecule is vibrating.

Polanyi Rules

QUESTION TEN

Polanyi rules state that vibrational energy activates a late transition state more efficiently than translational energy, and the opposite is true for an early transition states. (Guidelines but not rules set in stone.)

Mm10114 (talk) 20:50, 31 May 2018 (BST) Reference?

F + H₂

An exothermic reaction with an early transition state.
- F-H momentum = translational energy (fixed at -0.5)
- H-H momentum = vibrational energy
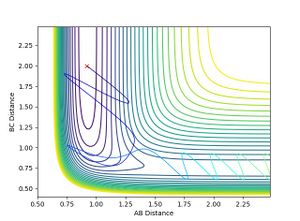
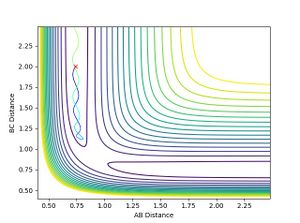
When H-H momentum = 0.3, i.e. vibrational energy is less than translational, the trajectory is reactive.

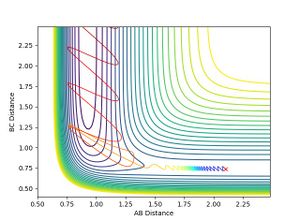
When H-H momentum = 3, i.e. vibrational energy is more than translational, the trajectory is unreactive.

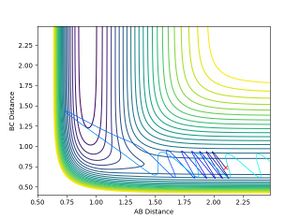
This shows that for an early transition state, the translational energy has a greater effect on the efficiency of reaction. i.e. the translational energy activates the TS more efficiently than vibrational energy leading to a reactive trajectory, agreeing with Polanyi rules.

H + HF

An endothermic reaction with a late transition state.
- F-H momentum = vibrational energy
- H-H momentum = translational energy
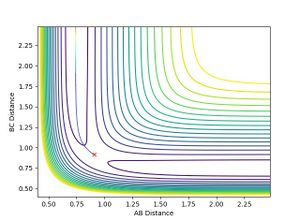
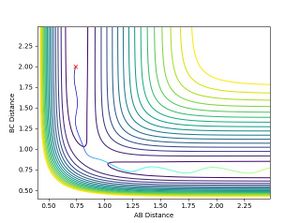
- When H-F momentum = 0.1 (LOW VIBRATIONAL ENERGY) and H-H momentum = -5 (HIGH TRANSLATIONAL ENERGY), the trajectory is unreactive.

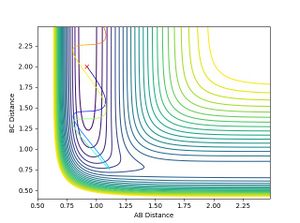
No matter how much the H-H momentum (translational energy) is increased, the trajectory will recross the barrier and return to reactants. This is because the vibrational energy, F-H momentum, is insufficient for the reaction to occur, therefore it follows Polanyi rules as it agrees that vibrational energy is more efficient for crossing late transition states. This is shown below:

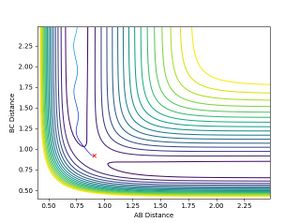
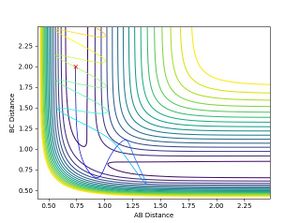
When H-F momentum = 7.5 (HIGH VIBRATIONAL ENERGY) and H-H momentum = -1.4 (LOW TRANSLATIONAL ENERGY), the trajectory is reactive.

H + H2 system