Molecular Reaction Dynamics: Application to triatomic systems

Application to the collision of H radical to H₂ molecule

Introduction

The reaction investigated in this section is a simple triatomic reaction involving diatomic hydrogen and hydrogen radical. The hydrogen are labelled as A, B and C.

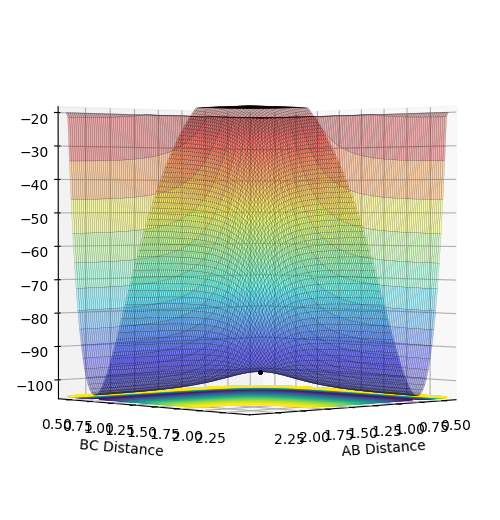
Significance of gradients in surface plots

The gradient of the minimum path potential energy is always equals to zero and is what the trajectory of the minimum energy path (MEP) follows. The minima is the lowest energy possible along the minimum path potential energy and is towards the entry and exit paths (the products/reactants) and in this case the same. The transition state is the maximum of the minimum energy path which is the saddle point of the potential energy. It satisfies the expression:

dV/dr₁=dV/dr₂=0

The transition state is shown on this surface plot which clearly shows the local maximum of the saddle point; the black dot marks exactly where the transition state is.

Jas213 (talk) 14:43, 28 May 2018 (BST) What about the second derivative?

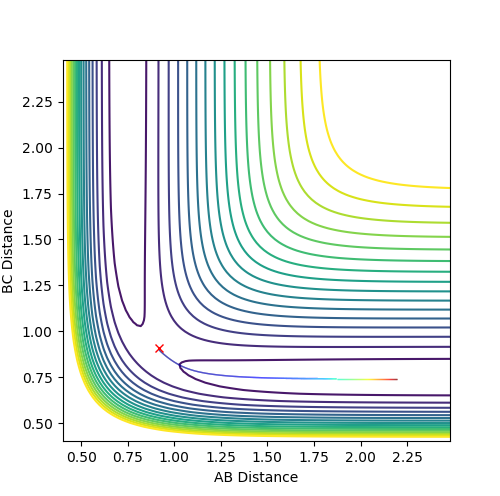
Determination of the transition state distances

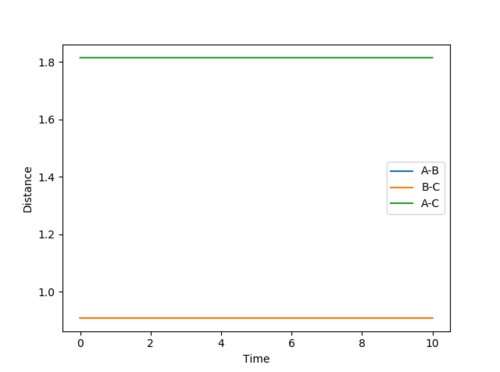
When the initial condition is at the transition state distance and has 0 movement, the system remains at rest and there is no fluctuation of the internuclear distances. From calculation, the estimate transition state distances between the hydrogen atoms is 0.907742 angstroms. When the initial conditions are set as such, the internuclear distances does not fluctuate.

Changing the calculation types and parameters

Minimum energy path (MEP)

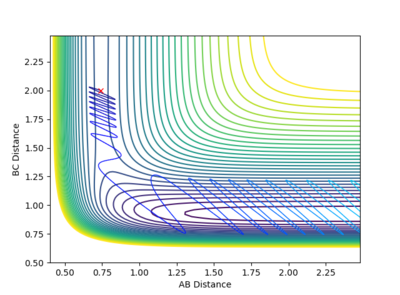
Because the transition state is the local maximum, nudging the setup either way will force it to collapse into the reactant/product. By nudging the setup very slightly to one side and changing the calculation type to MEP, the MEP reaction pathway can be determined as the trajectory follows a very slow motion.

By nudging AB distance by 0.01 angstroms (0.917742 angstroms) and keeping BC distance the same, the reaction proceeds simply to H_a + H_bH_c down its minimum.

The difference between MEP and dynamic type calculations

In minimum energy path (MEP), the atoms move a lot slower than the dynamic calculation type and does not show oscillation motion. The final A-C distance value for MEP approaches 2.0 units however the dynamic trajectory is approximately 10.0 units in the same amount of time (2.5 time units), this is due to MEP calculation type modelling infinitely slow motion down the MEP.

Changing the parameters

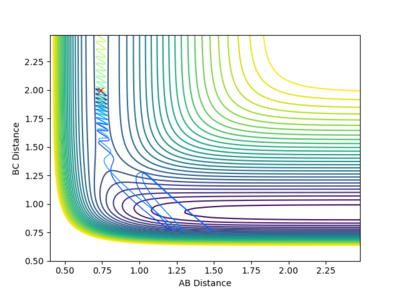
Given that all three atoms are initially at rest, when r₁=0.918=r_ts+0.01, and r₂=0.908=r_ts, the final values when using dynamic calculation type (t=2.5 time units) are:

r₁=9.03 and r₂=0.75

p₁=2.48 (constant) and p₂=1.22 (on average)

If we were to to swap the initial values of r₁ and r₂, the calculated values will be the same but swapped such that r₁ becomes r₂ and vice versa.

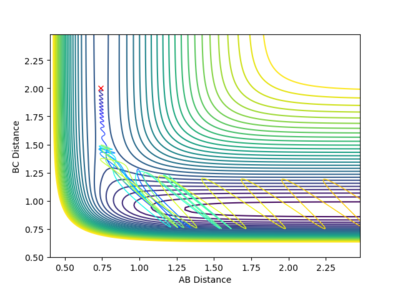
By setting up the initial positions as the calculated final positions from above but with the negative value of the calculated momentum, essentially the atoms will approach each other and achieve the transition state at the same amount of time as the motions are played back. This is the inversion of momentum procedure which follows a time symmetrical pathway.

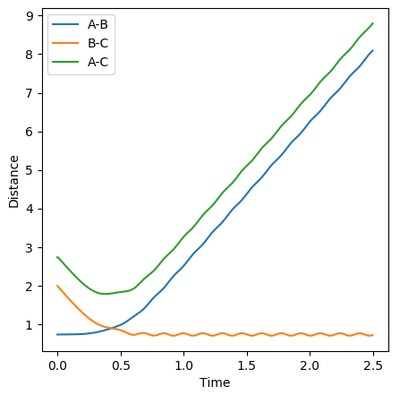
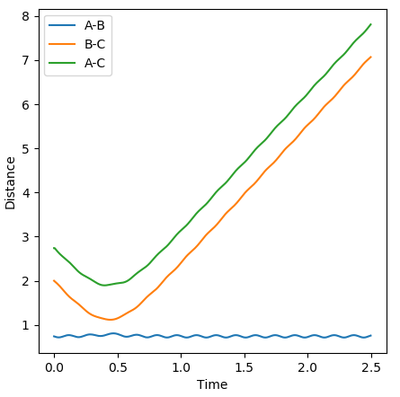
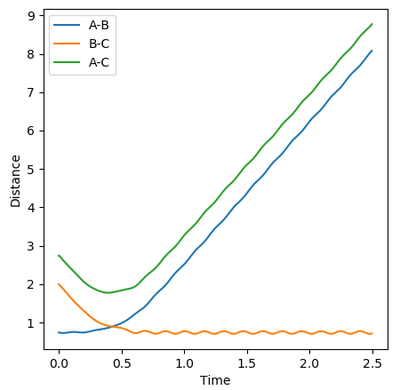
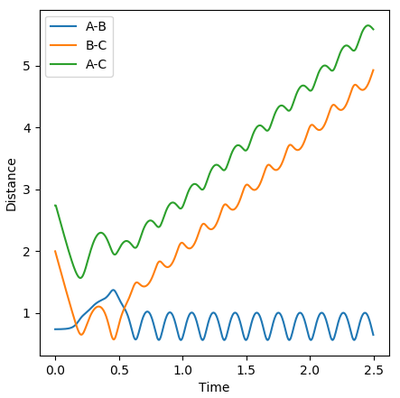
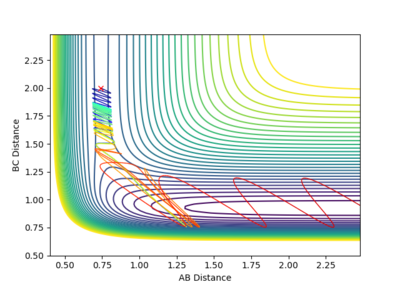
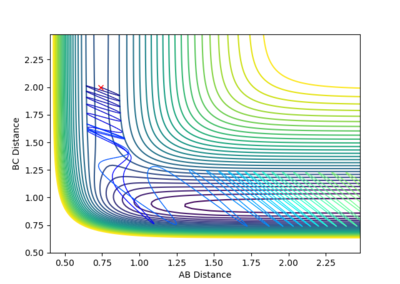
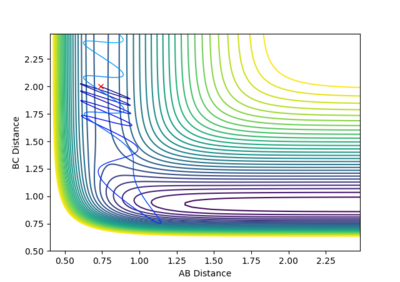
Reactive and Unreactive trajectories

Collisions need to have enough kinetic energy to be able to go over the activation energy barrier and form the product and so one can assume that beyond the threshold momentum, the reaction will be successful as it has enough kinetic energy, but this is not always the case. The table below shows the total energy of the system and determine if the reaction is successful or not.

p₁	p₂	Total energy	Status	description
-1.25	-2.5	-99.018	reactive	In this calculation, the momentum/energy of the system is enough such that hydrogen C can cross the barrier and form a stable bond with hydrogen B, causing the value of BC to drop and stablise; in consequence atom A is ejected and hence the increase in AB and AC distances.
-1.5	-2.0	-100.456	unreactive	In this calculation, the momentum/energy of the system is not enough for hydrogen C to cross the barrier and so the distance BC although decreases at first as hydrogen C approaches hydrogen B, it increases again after 0.5 time units as hydrogen C is repelled away therefore an unsuccessful reaction.
-1.5	-2.5	-98.956	reactive	Again as expected, as the total energy of the system is higher than the first calculation, hydrogen C has enough energy to cross the barrier and form a successful bond with hydrogen B, stablising the distance of BC to oscillate around 0.7 angstroms while ejecting hydrogen A.
-2.5	-5.0	-84.956	unreactive	This calculation demonstrates barrier recrossing; the total energy of the system is higher than the first calculation and initially hydrogen C does cross the barrier but then it gets ejected out again as it recrosses the transition state barrier again, increasing the value of BC again.
-2.5	-5.2	-83.416	reactive	Looking superficially, this calculation goes as expected, the momentum/energy of the system is high enough so that hydrogen C can cross the barrier and form the BC bond. The actual calculation shows that the reaction crosses the transition state barrier three times before the BC bond is formed. The extra energy is absorbed into the vibrational energy as demonstrated by the high oscillation of BC distance compared to the first calculation.

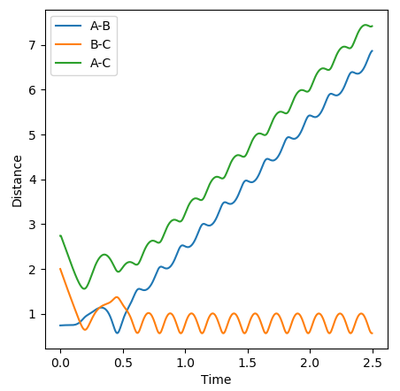
Despite the fourth calculation having a higher total energy than the first calculation on the table above, the reaction is unsuccessful, demonstrating that higher kinetic energy does not always mean the reaction will be successful; this can be attributed to barrier recrossing. For all graphs the distance between atom B and C is the new bond that is going to be formed. A successful bond is made when the distance oscillates between a value around 0.7 angstroms.

Jas213 (talk) 14:46, 28 May 2018 (BST) First sentence is a good start to an overall conclusion of what you learned from the table.

Transition state theory

Transition state theory (TST) assumes that chemical reactions, whether reversible or irreversible, undergoes a quasi-equilibrium with the transition state and it assumes that there is no quantum tunneling effects; if the system does not have enough energy to cross the activation energy then the reaction will not occur. TST also assumes that the reaction will proceed at the lowest possible energy and once pass the energy barrier, will not fall recross the barrier back to the reactant. Because of this, it fails to predict barrier recrossing effect as the transition state formed at higher temperatures (the particles involved have high momentum) and the transition state can be a lot higher than the lowest possible energy. The kinetics predicted by TST at higher temperature is therefore going to be higher than experimental values as it does not take into account barrier recrossing.

Jas213 (talk) 14:46, 28 May 2018 (BST) Where are your references for this?

Application on F-H-H System

Introduction

The reaction investigated in this section is the reaction of fluorine radical to diatomic hydrogen to form hydrogen fluoride and hydrogen radical. The reaction will be treated as "reversible". In the calculation, Atom A and B are hydrogen atoms and atom C is the fluorine radical.

Potential Energy Surface Inspection

Reaction Energetics

In the reaction F + H₂ ⇌ HF + H, the forward reaction is exothermic and the reversed reaction is therefore endothermic; this is due to the formation of HF bond which is stronger (569 kj/mol) compared to HH bond (435 kj/mol).

Jas213 (talk) 14:47, 28 May 2018 (BST) kJ/mol

The transition state bond lengths of the system is determined to be approximately these values:

HH=0.745 angstroms

HF=1.811 angstroms

The calculated activation energy for the forward reaction, F + H₂, is 0.268 kcal/mol whilst the reversed reaction,HF + H, is 30.247 kcal/mol rendering this reaction essentially irreversible at room temperature.

Jas213 (talk) 14:48, 28 May 2018 (BST) Correct, but how did you obtain these values? Where are your MEP plots for this?

Reaction Dynamics

Conservation of Energy

Given that A and B are hydrogen atoms and C is a fluorine atom in a linear collision trajectory, setting AB distance to 0.75 and BC distance to 3 angstroms and the BC momentum of -1.2 units, the reaction is successful and because of the strong attraction between B and C, this causes atom A to be ejected at a relatively high speed and the vibration of H-F bond to be quite vigorous. Collectively, the vibration and translation is observed in the form of heat. By using a calorimeter to measure the temperature difference after the reaction, the thermal energy observed can be compared to the calculated energy values. The energy released as vibrational mode could be measured by measuring the infrared radiation emission at the H-F stretch region.

Polanyi's rules

Setting up the calculation to be towards the reactants of the forward reaction (F radical and diatomic hydrogen), the H-H bond length is set as 0.74 and F-H distance to be 2.0 angstroms. The initial translational momentum is set to be -0.5 and the vibrational momenta for H₂ will be -3, -2, -1, 0, 1, 2 and 3 units:

p_HH	Energy	description	Status
-3	-96.159	The system has enough energy to go over the activation energy (cross the transition state boundary) but collapsed back through the transition state to the reactants via barrier recrossing.	unreactive
-2	-100.659	The system has just the right amount of energy to pass through the transition state and fall down to the exit channel, yielding the product.	reactive
-1	-103.159	The reaction initially tips over to the exit channel but then it collapsed back through the transition state to the reactant via barrier recrossing.	unreactive
0	-103.659	The reaction has enough energy to pass through the transition state and although at first glance seems to be a straightforward reaction, the system actually crosses through the transition state many times before it is able to fall to the exit channel yielding the products.	reactive
1	-102.159	Similar to when P_HH is equivalent to 0, the reaction crosses the transition state several times before falling to the exit channel yielding the products.	reactive
2	-98.659	Similar to when P_HH is equivalent to 0, the reaction crosses the transition state a couple of times before falling to the exit channel yielding the products.	reactive
3	-93.159	The trajectory resembles when P_HH is -3, the reaction initially looks as if it would be successful but it crosses back through the transition state and collapse to the entrance side yielding the reactants.	unreactive

The higher the absolute value of P_HH, the higher the total energy in the system, all with way more energy than the activation energy and some reactions are successful while some are not due to the unpredictability of barrier recrossing. Higher vibrational energy and therefore the total energy does not always determine the success of this particular reaction which contradicts with the TST.

Changing the initial value slightly so that P_HH is -0.1 and the momentum of F radical is -0.8 gives this result:

Despite the total energy of the system being significantly lower than most of the trajectory calculations above, the reaction is successful demonstrating that the translational energy is more efficient than the vibrational energy in this case.

On the flip side, setting up the calculation so that the reaction proceeds backwards (from H + HF to H₂ + F), the initial condition to a successful reaction would be this:

Jas213 (talk) 14:50, 28 May 2018 (BST) Good reasoning, shows clear understanding of the material studied and the proportions of vibrational and translational energy.

The initial energy in this calculation is relatively low but yields a successful reaction. When looking at how the energy is distributed, the vibrational mode is much higher than the translational mode, swapping these values such that the total energy of the system is the same will result in an unsuccessful reaction.

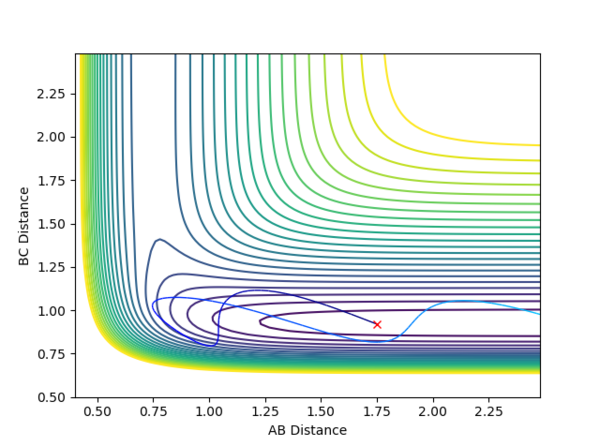
In the case of the reverse reaction, a high translational fraction of the same total energy is not as efficient as high vibrational fraction; at a reasonably low energy just above needed for activation, the translation motion just gets repelled back without crossing through the transition state where as the high vibration allows the system to cross through the exit channel. By applying the inversion of momentum procedure, if high vibration low translation system is successful for the reverse reaction, the forward reaction would be opposite; high translation low vibration tend to be more successful.

To conclude, this demonstrates Polanyi's empirical rule which states that for a reaction with proximal transition state, the momentum is more deterministic than vibration for the reactivity and for reactions with late transition state, the opposite applies. Since the transition state is a lot closer to F + H₂, the forward reaction will be more determined by the momentum and the reverse reaction will depend more on the vibrational energy.

Jas213 (talk) 14:53, 28 May 2018 (BST) You mean translational energy when you say momentum? Both p1 and p2 are momenta. Correct conclusion, however sadly no references given for Polanyi's rules.